Repaso

Analizando opinión pública

library(rio)
peru23 = import("bases/PER_2023_LAPOP_AmericasBarometer_v1.0_w.sav")

Describir una variable numérica

library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

peru23 %>%
  summarise(Promedio_Matri=mean(d6, na.rm=T), 
            Mediana_Matri=median(d6, na.rm=T))

##   Promedio_Matri Mediana_Matri
## 1       4.082731             3

peru23 %>%
  summarise(Promedio_Adopcion=mean(d7a, na.rm=T), 
            Mediana_Adopcion=median(d7a, na.rm=T))

##   Promedio_Adopcion Mediana_Adopcion
## 1          4.023841                3

Visualización variable numérica

library(ggplot2)
ggplot(peru23, aes(x=d6))+
  geom_histogram(binwidth = 1)+
  xlab("Aprobación matrimonio igualitario") +
  ylab("Frecuencia")+
  theme_minimal()

## Warning: Removed 12 rows containing non-finite outside the scale range
## (`stat_bin()`).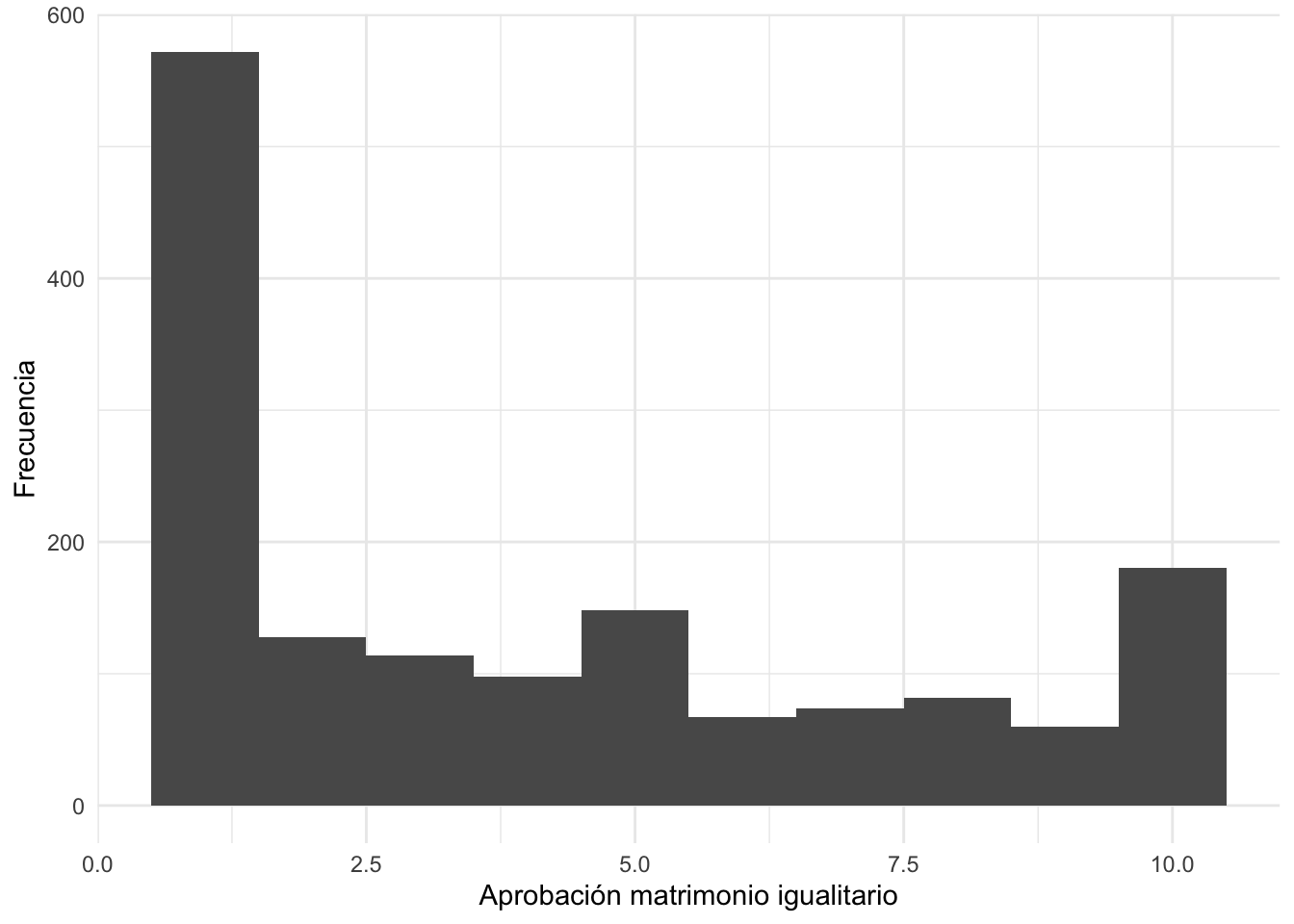

ggplot(peru23, aes(x=d7a))+
  geom_histogram(binwidth = 1)+
  xlab("Aprobación adopción") +
  ylab("Frecuencia")+
  theme_minimal()

## Warning: Removed 780 rows containing non-finite outside the scale range
## (`stat_bin()`).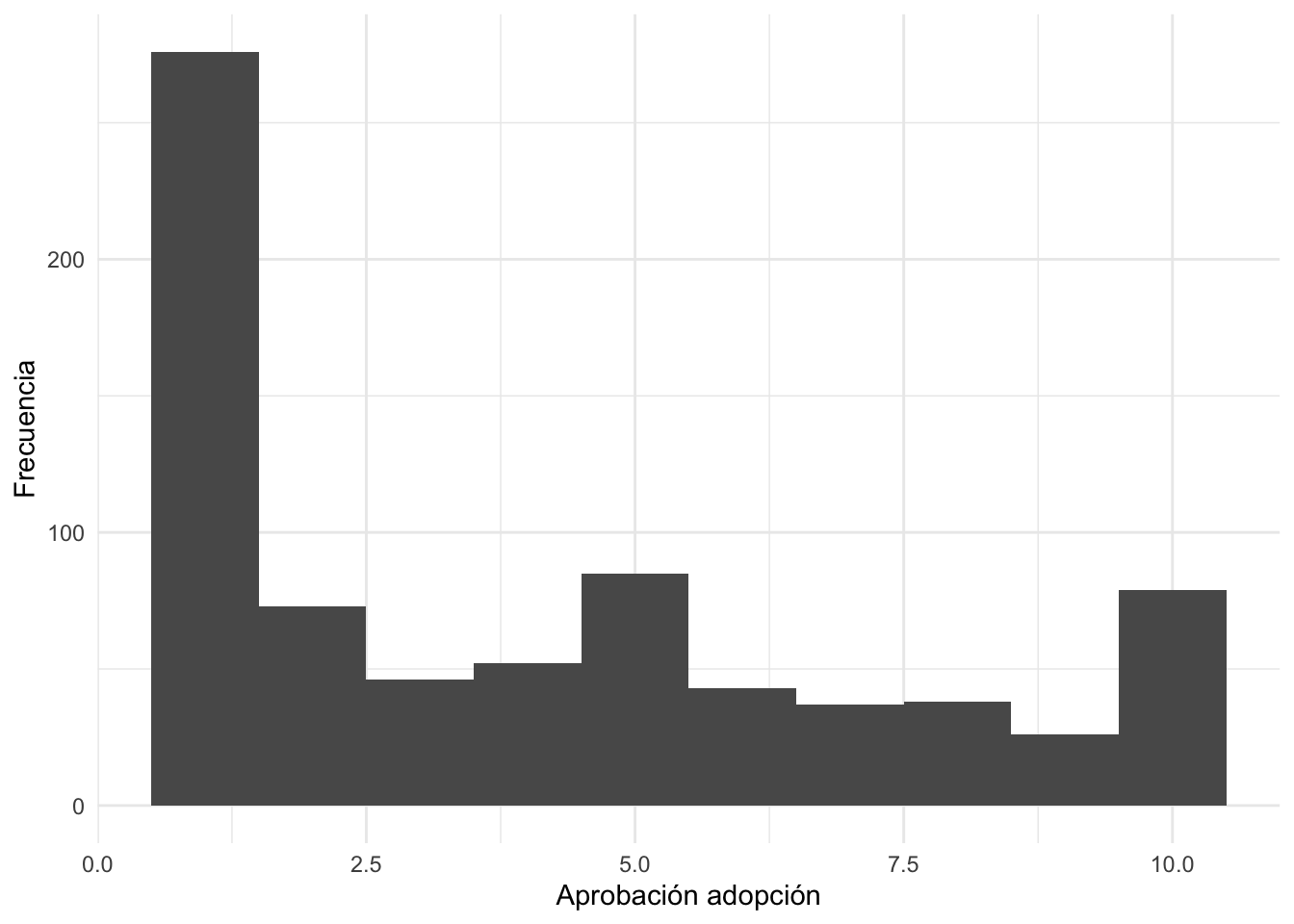

Comparando variable numérica entre grupos

peru23 = peru23 %>%
  mutate(educ = case_when(
    edre <= 3 ~ 1,
    edre == 4 ~ 2,
    edre == 5 ~ 3,
    edre == 6 ~ 4,
    ))

peru23 = peru23 %>%
  mutate(educ2 = factor(educ, labels=c("Colegio incompleto", 
                                       "Colegio completo", 
                                       "Superior incompleta", 
                                       "Superior completa")))

peru23 %>%
  group_by(educ2) %>%
  summarise(Promedio_Matri=mean(d6, na.rm=T), 
            Mediana_Matri=median(d6, na.rm=T))

## # A tibble: 4 × 3
##   educ2               Promedio_Matri Mediana_Matri
##   <fct>                        <dbl>         <dbl>
## 1 Colegio incompleto            3.24             1
## 2 Colegio completo              3.97             3
## 3 Superior incompleta           4.83             5
## 4 Superior completa             4.34             4

Graficando la comparación

ggplot(peru23, aes(y=d6, x=educ2))+
  geom_boxplot()+
  ylab("Aprobación matrimonio igualitario")+
  xlab("Nivel educativo")+
  theme_get()

## Warning: Removed 12 rows containing non-finite outside the scale range
## (`stat_boxplot()`).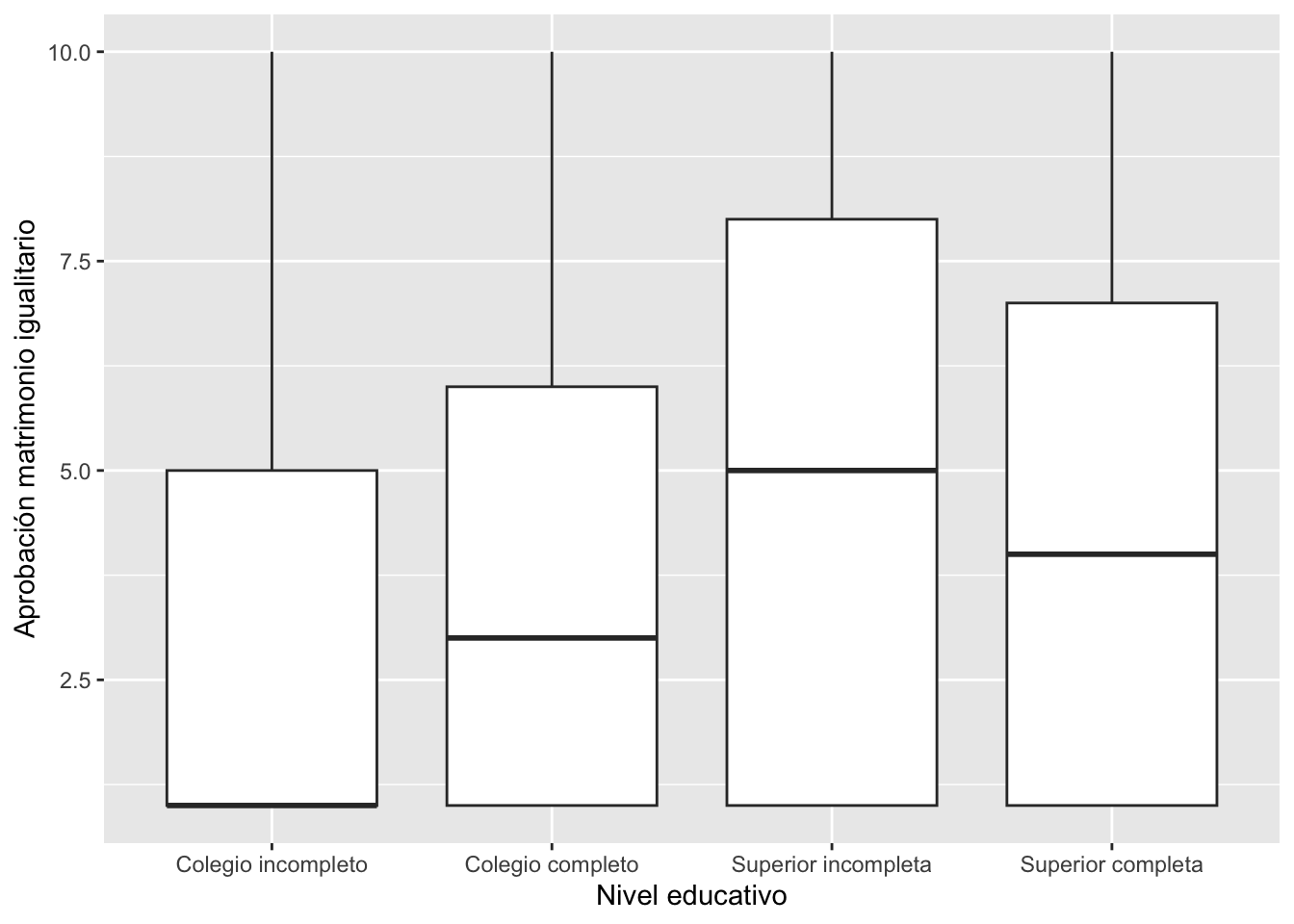

Describir una variable categórica

peru23 = peru23 %>%
  mutate(aborto = factor(w14a, labels=c("Sí se justifica", 
                                          "No se justifica")))

tabla1 = peru23 %>%
  filter(aborto == "Sí se justifica" | aborto == "No se justifica") %>%
  count(Aborto = aborto, name="Frecuencia")
tabla1

##            Aborto Frecuencia
## 1 Sí se justifica       1090
## 2 No se justifica        414

tabla1 = tabla1 %>%
  mutate(Porcentaje = (Frecuencia / sum(Frecuencia)*100 ))
tabla1

##            Aborto Frecuencia Porcentaje
## 1 Sí se justifica       1090    72.4734
## 2 No se justifica        414    27.5266

Visualización variable factor

graf1 = ggplot(tabla1, aes(x=Aborto,y=Porcentaje))+
  geom_bar(stat="identity", width=0.5)
graf1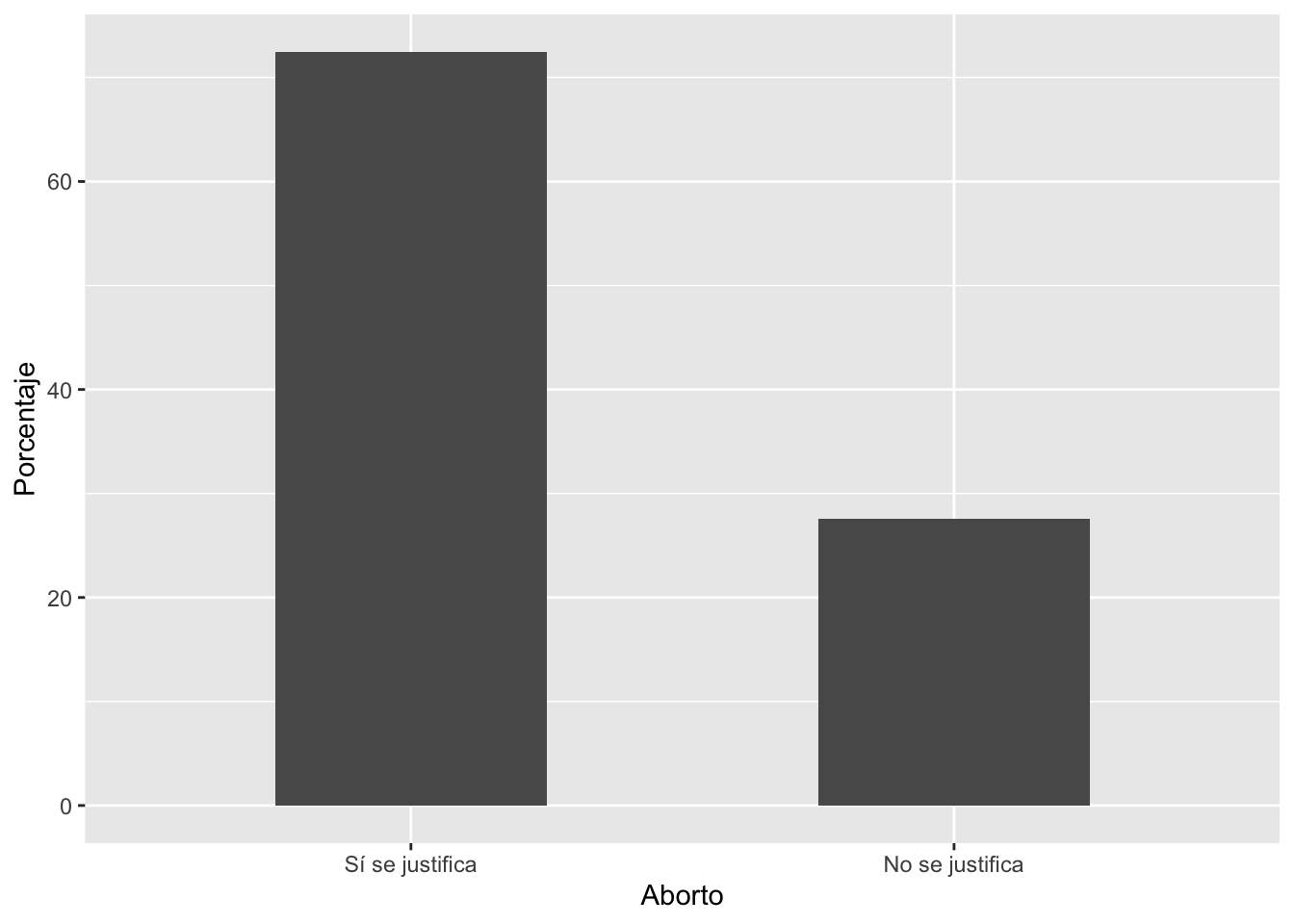

Comparando variable factor entre grupos

tabla2 = peru23 %>%
  filter(aborto == "Sí se justifica" | aborto == "No se justifica") %>%
  group_by(educ2) %>%
  count(Aborto = aborto, name="N") %>%
  mutate(total = sum(N), 
         Por = N / total * 100, 
         err = sqrt(Por*(100-Por)/N), 
         liminf = Por - 1.96*err, 
         limsup = Por + 1.96*err)
tabla2

## # A tibble: 8 × 8
## # Groups:   educ2 [4]
##   educ2               Aborto              N total   Por   err liminf limsup
##   <fct>               <fct>           <int> <int> <dbl> <dbl>  <dbl>  <dbl>
## 1 Colegio incompleto  Sí se justifica   200   305  65.6  3.36   59.0   72.2
## 2 Colegio incompleto  No se justifica   105   305  34.4  4.64   25.3   43.5
## 3 Colegio completo    Sí se justifica   339   497  68.2  2.53   63.3   73.2
## 4 Colegio completo    No se justifica   158   497  31.8  3.70   24.5   39.1
## 5 Superior incompleta Sí se justifica   210   268  78.4  2.84   72.8   83.9
## 6 Superior incompleta No se justifica    58   268  21.6  5.41   11.0   32.2
## 7 Superior completa   Sí se justifica   341   434  78.6  2.22   74.2   82.9
## 8 Superior completa   No se justifica    93   434  21.4  4.25   13.1   29.8

tabla2 = tabla2[-c(2,4, 6, 8),]

Graficando la comparación

graf2 = ggplot(tabla2, aes(x=educ2, y=Por))+
  geom_bar(stat="identity")+
  geom_text(aes(label=paste(round(Por, 1))), vjust=-1, size=3)+
  labs(x="Sexo", y="Porcentaje que justifica aborto")+
  theme_classic()
graf2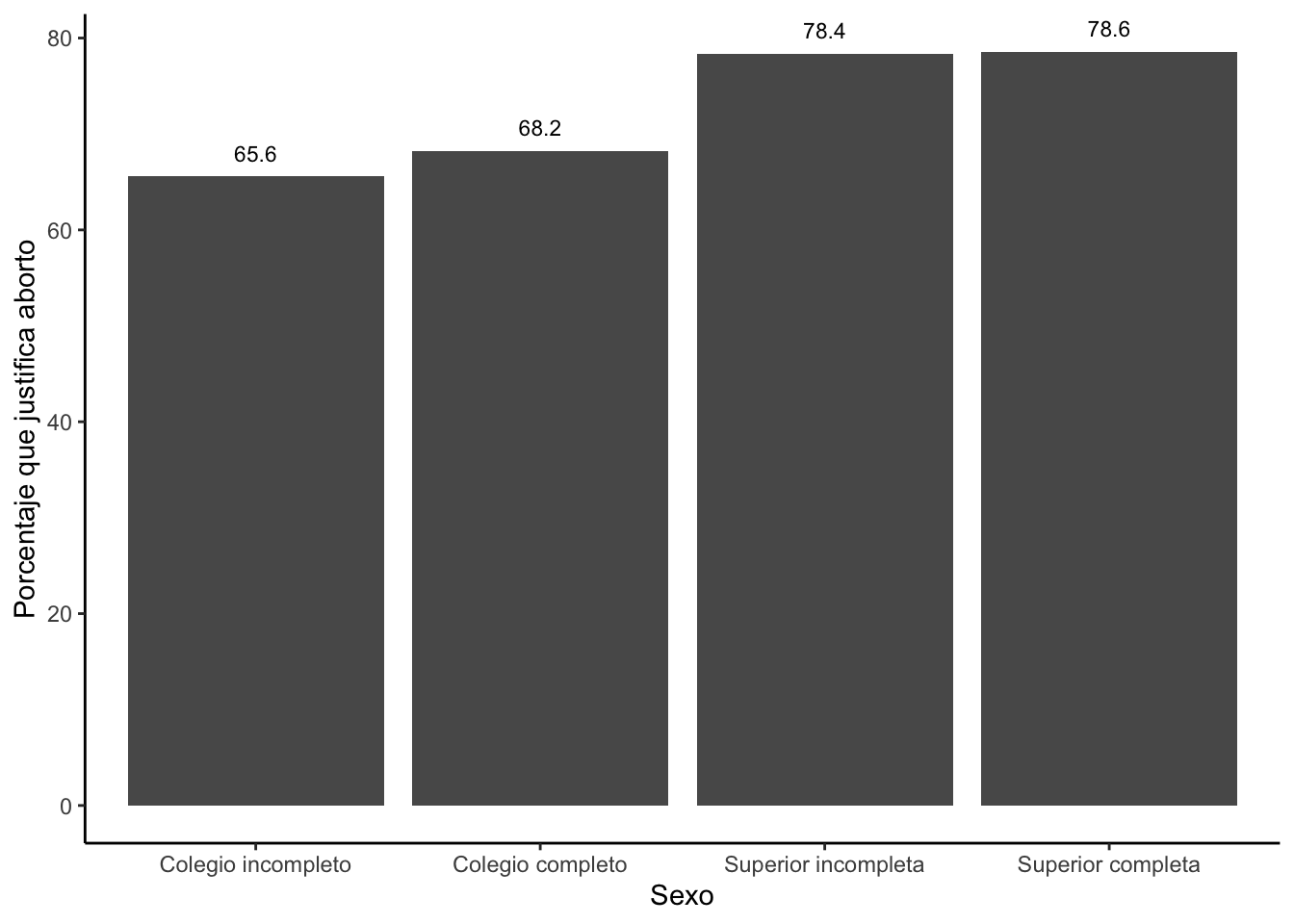

Comparando variables numéricas con intervalos de confianza

library(lsr)
tabla3 = peru23 %>%
  group_by(educ2) %>%
  summarise(Promedio_Matri=mean(d6, na.rm=T), 
            Desv_Matri=sd(d6, na.rm=T),
            liminf = ciMean(d6, na.rm=T)[1],
            limsup = ciMean(d6, na.rm=T)[2])
tabla3

## # A tibble: 4 × 5
##   educ2               Promedio_Matri Desv_Matri liminf limsup
##   <fct>                        <dbl>      <dbl>  <dbl>  <dbl>
## 1 Colegio incompleto            3.24       3.05   2.90   3.58
## 2 Colegio completo              3.97       3.15   3.70   4.25
## 3 Superior incompleta           4.83       3.41   4.42   5.24
## 4 Superior completa             4.34       3.29   4.04   4.65

Graficando comparación de IC para variable numérica

graf3 = ggplot(tabla3, aes(x=educ2, y=Promedio_Matri))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=round(Promedio_Matri, 1)), vjust=-2.8, size=3)+
  xlab("Nivel educativo") + ylab("Aprobación matrimonio igualitario")+
  ylim(0, 6)
graf3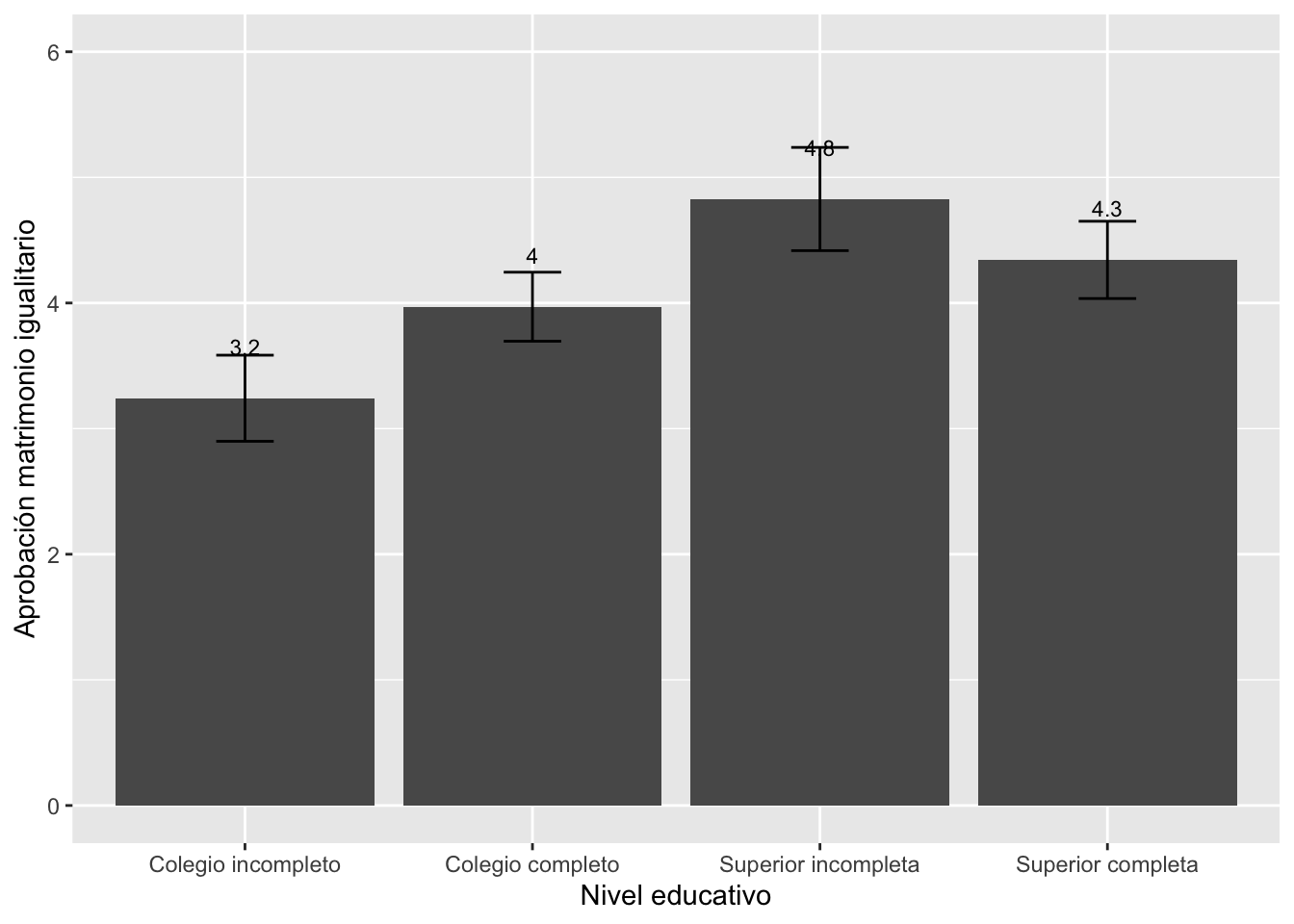

Comparando proporciones con intervalos de confianza

tabla4 = peru23 %>%
  filter(aborto == "Sí se justifica" | aborto == "No se justifica") %>%
  group_by(educ2) %>%
  count(Aborto = aborto, name="N") %>%
  mutate(total = sum(N), 
         Por = N / total * 100,
         err = sqrt(Por*(100-Por)/N), 
         liminf = Por - 1.96*err, 
         limsup = Por + 1.96*err)
tabla4

## # A tibble: 8 × 8
## # Groups:   educ2 [4]
##   educ2               Aborto              N total   Por   err liminf limsup
##   <fct>               <fct>           <int> <int> <dbl> <dbl>  <dbl>  <dbl>
## 1 Colegio incompleto  Sí se justifica   200   305  65.6  3.36   59.0   72.2
## 2 Colegio incompleto  No se justifica   105   305  34.4  4.64   25.3   43.5
## 3 Colegio completo    Sí se justifica   339   497  68.2  2.53   63.3   73.2
## 4 Colegio completo    No se justifica   158   497  31.8  3.70   24.5   39.1
## 5 Superior incompleta Sí se justifica   210   268  78.4  2.84   72.8   83.9
## 6 Superior incompleta No se justifica    58   268  21.6  5.41   11.0   32.2
## 7 Superior completa   Sí se justifica   341   434  78.6  2.22   74.2   82.9
## 8 Superior completa   No se justifica    93   434  21.4  4.25   13.1   29.8

tabla4 = tabla4[-c(2,4,6,8),]

graf4 = ggplot(tabla4, aes(x=educ2, y=Por))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=paste(round(Por, 1))), vjust=-3, size=3)+
  labs(x="Nivel educativo", y="Porcentaje que justifica el aborto",
       caption="Barómetro de las Américas por LAPOP, 2021")+
  theme_classic()
graf4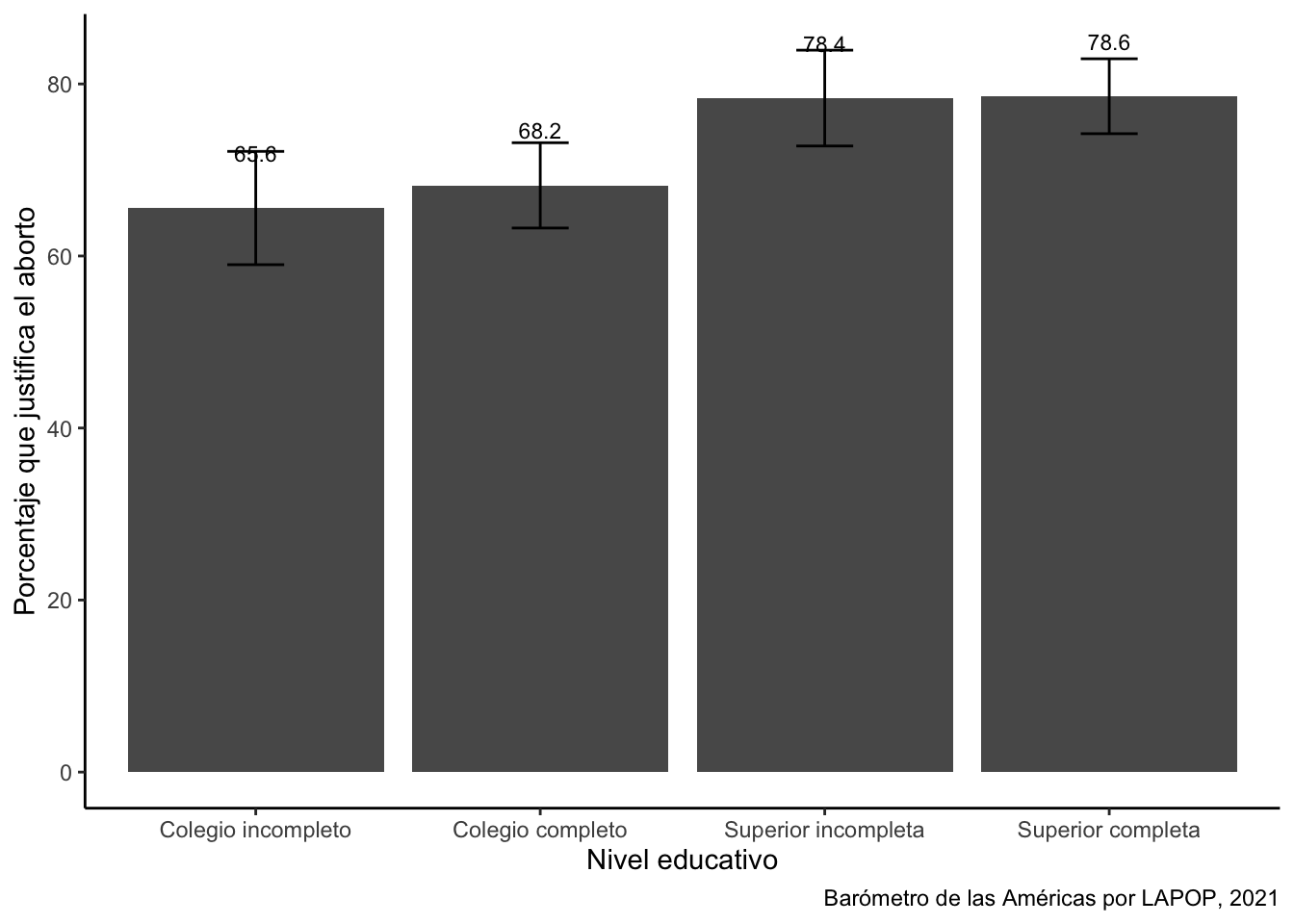

Prueba de significancia para variables numéricas dicotómicas

peru23 = peru23 %>%
  mutate(sexo = factor(q1tc_r, labels=c("Hombre", "Mujer")))

tabla5 = peru23 %>%
  group_by(sexo) %>%
  summarise(Promedio_Matri=mean(d6, na.rm=T), 
            Desv_Matri=sd(d6, na.rm=T),
            liminf = ciMean(d6, na.rm=T)[1],
            limsup = ciMean(d6, na.rm=T)[2])
tabla5

## # A tibble: 3 × 5
##   sexo   Promedio_Matri Desv_Matri liminf limsup
##   <fct>           <dbl>      <dbl>  <dbl>  <dbl>
## 1 Hombre           3.79       3.17  3.56    4.01
## 2 Mujer            4.38       3.32  4.14    4.61
## 3 <NA>             4.6        3.36  0.426   8.77

t.test(d6 ~ sexo, data = peru23)

## 
##  Welch Two Sample t-test
## 
## data:  d6 by sexo
## t = -3.5255, df = 1510.5, p-value = 0.0004353
## alternative hypothesis: true difference in means between group Hombre and group Mujer is not equal to 0
## 95 percent confidence interval:
##  -0.9142069 -0.2605747
## sample estimates:
## mean in group Hombre  mean in group Mujer 
##             3.789267             4.376658

Prueba de significancia para variables numéricas politómicas

anova1 = aov(peru23$d6~peru23$educ2)
summary(anova1)

##                Df Sum Sq Mean Sq F value   Pr(>F)    
## peru23$educ2    3    401  133.66    12.9 2.52e-08 ***
## Residuals    1519  15737   10.36                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 12 observations deleted due to missingness

compara = TukeyHSD(anova1)
compara

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = peru23$d6 ~ peru23$educ2)
## 
## $`peru23$educ2`
##                                              diff        lwr       upr
## Colegio completo-Colegio incompleto     0.7285841  0.1293353 1.3278329
## Superior incompleta-Colegio incompleto  1.5858853  0.8926390 2.2791316
## Superior completa-Colegio incompleto    1.1012851  0.4859595 1.7166106
## Superior incompleta-Colegio completo    0.8573012  0.2313543 1.4832480
## Superior completa-Colegio completo      0.3727009 -0.1656712 0.9110730
## Superior completa-Superior incompleta  -0.4846002 -1.1259549 0.1567545
##                                            p adj
## Colegio completo-Colegio incompleto    0.0097272
## Superior incompleta-Colegio incompleto 0.0000000
## Superior completa-Colegio incompleto   0.0000267
## Superior incompleta-Colegio completo   0.0024820
## Superior completa-Colegio completo     0.2831338
## Superior completa-Superior incompleta  0.2104477

Graficando la comparación politómica

compara.df = as.data.frame(compara[1])
compara.df$compara = rownames(compara.df)

graf5 = ggplot(compara.df, aes(x=compara, y=peru23.educ2.diff))+
  geom_errorbar(aes(ymin=peru23.educ2.lwr, ymax=peru23.educ2.upr), 
                width=0.2)+
  geom_text(aes(label=paste(round(peru23.educ2.diff, 1))), 
            vjust=-1, size=3)+
  xlab("Comparación") + ylab("Diferencia")+
  ylim(-3, 3) +
  coord_flip() +
  geom_hline(yintercept = 0, color = "red", linetype="dotted") +
  theme_classic()
graf5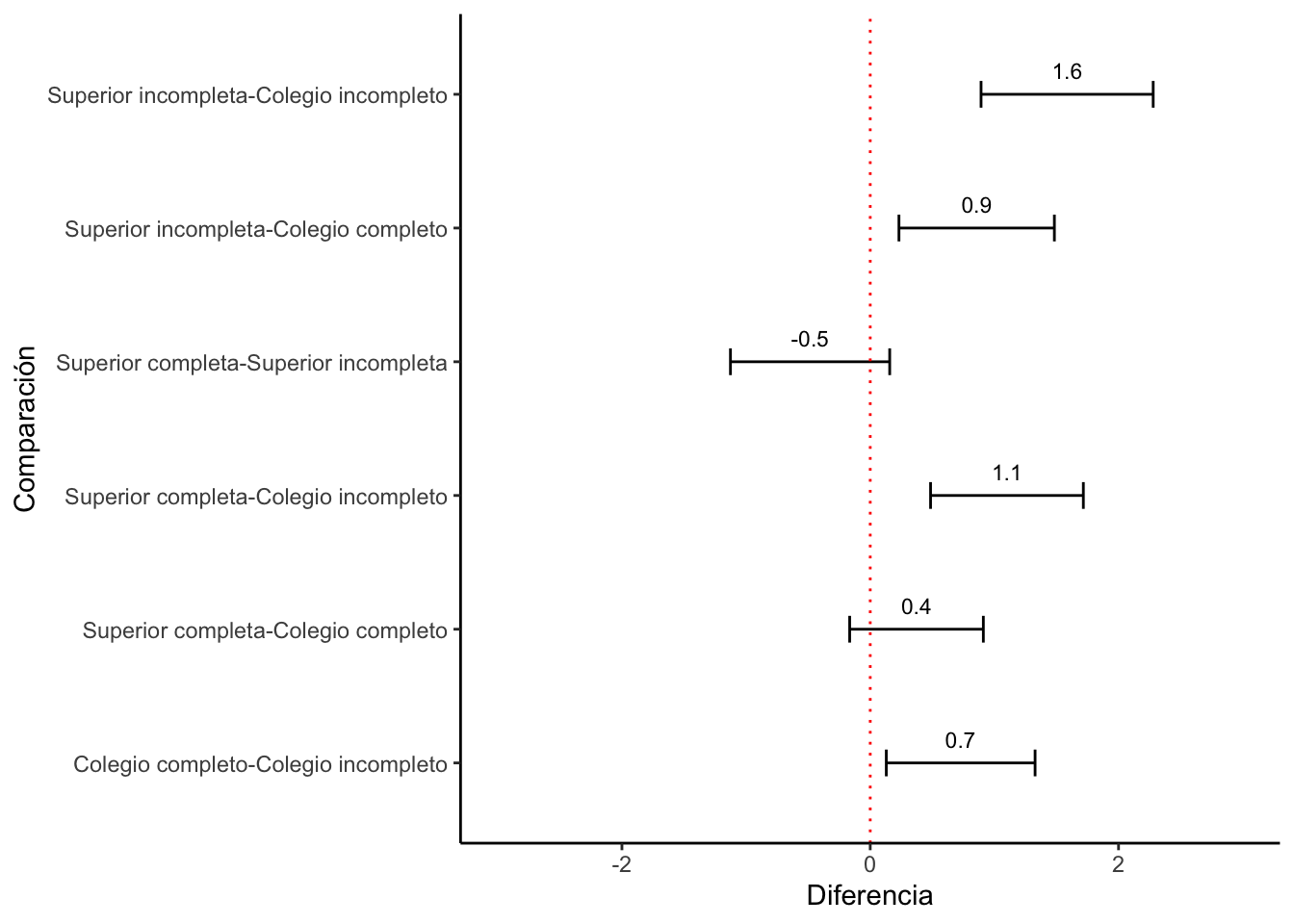

Tabla de contingencia

tabla6 = table(peru23$aborto, peru23$educ2)
tabla6

##                  
##                   Colegio incompleto Colegio completo Superior incompleta
##   Sí se justifica                200              339                 210
##   No se justifica                105              158                  58
##                  
##                   Superior completa
##   Sí se justifica               341
##   No se justifica                93

tabla7 = tabla6 %>%
  prop.table(2) %>%
  round(3)*100 
tabla7

##                  
##                   Colegio incompleto Colegio completo Superior incompleta
##   Sí se justifica               65.6             68.2                78.4
##   No se justifica               34.4             31.8                21.6
##                  
##                   Superior completa
##   Sí se justifica              78.6
##   No se justifica              21.4

Prueba de significancia para proporciones: Chi cuadrado

prop.test(c(803, 759), c(1610,1412))

## 
##  2-sample test for equality of proportions with continuity correction
## 
## data:  c(803, 759) out of c(1610, 1412)
## X-squared = 4.3759, df = 1, p-value = 0.03645
## alternative hypothesis: two.sided
## 95 percent confidence interval:
##  -0.075118749 -0.002436544
## sample estimates:
##    prop 1    prop 2 
## 0.4987578 0.5375354

prueba1 = chisq.test(peru23$aborto, peru23$educ2)
prueba1

## 
##  Pearson's Chi-squared test
## 
## data:  peru23$aborto and peru23$educ2
## X-squared = 24.55, df = 3, p-value = 1.917e-05

ggplot(data=tabla4, aes(x=Aborto, y=Por, fill=educ2))+
  geom_bar(position = "dodge", stat="identity")+
  geom_text(aes(label=paste(round(Por, 1), "%", sep="")), 
            position = position_dodge(width = 0.9), 
            vjust=0, size = 3)+
  labs(x="Justificación del aborto", y="Porcentaje", 
       fill="Nivel educativo")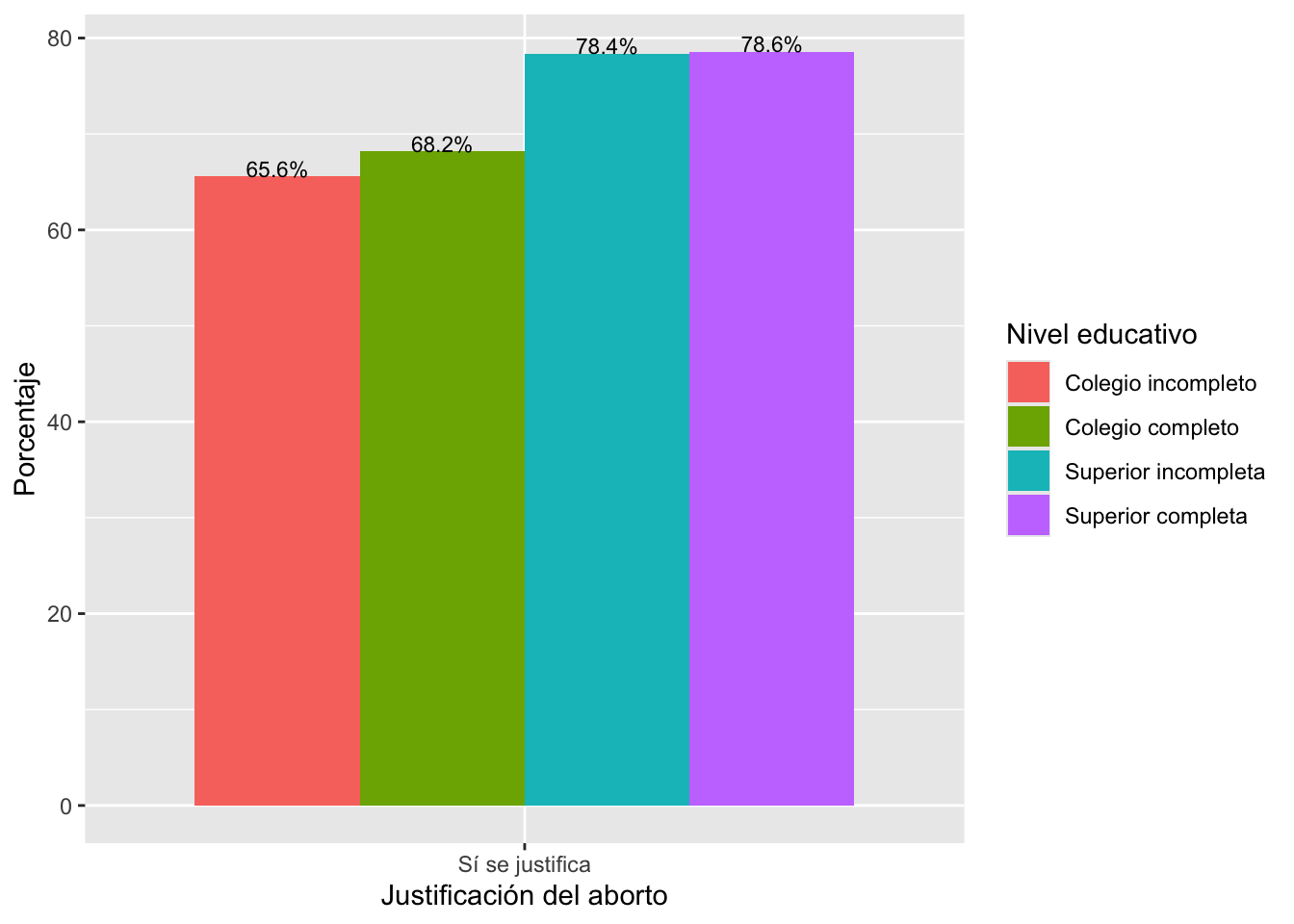

ggplot(data=tabla4, aes(x=educ2, y=Por, fill=Aborto))+
  geom_bar(position="stack", stat="identity")+
  geom_text(aes(label=paste(round(Por, 1), "%", sep="")), 
            position = position_stack(), vjust=1, size = 3)+
  labs(x="Nivel educativo", y="Porcentaje", fill="Justificación del aborto")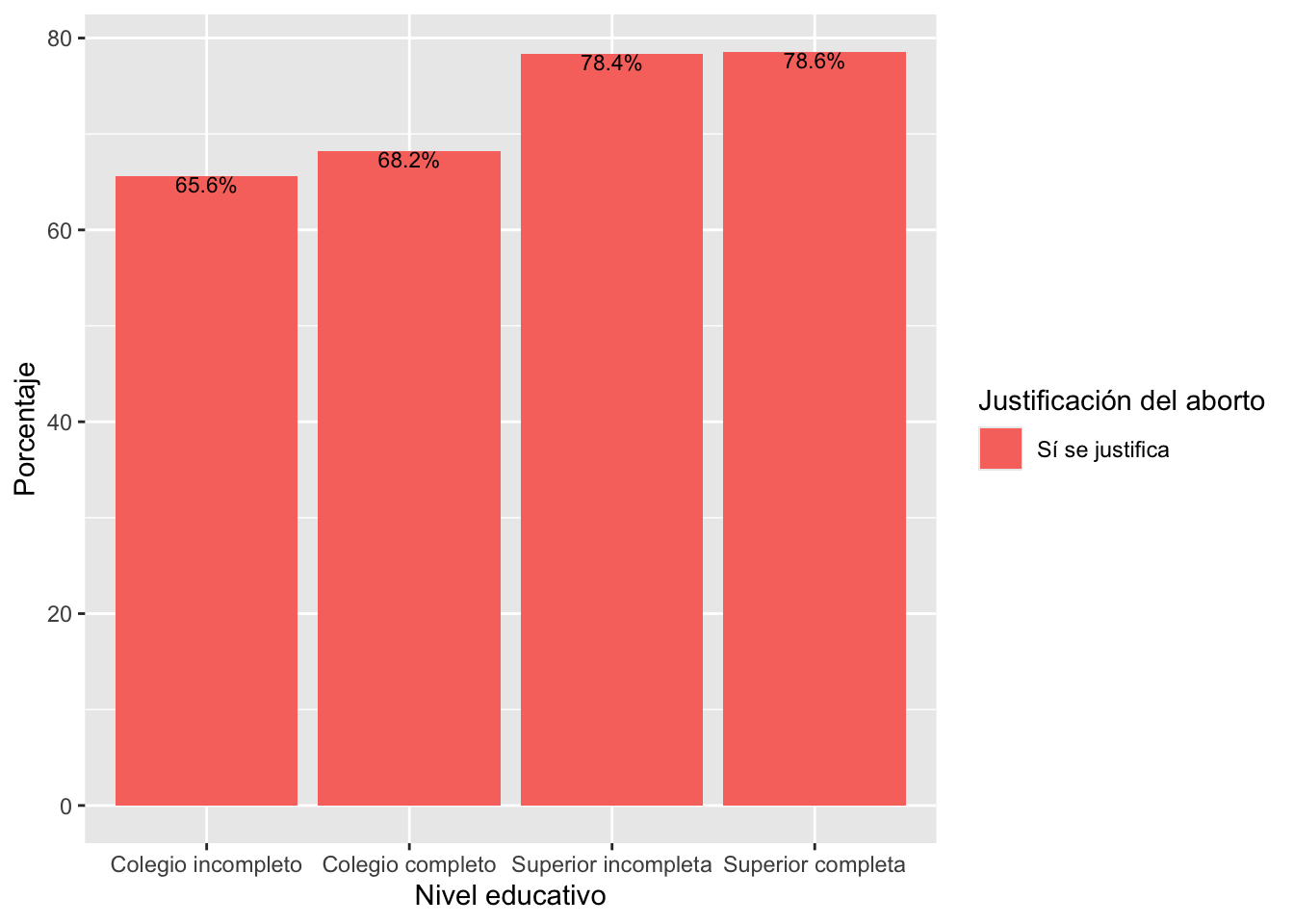

Relación entre dos variables numéricas

ggplot(peru23, aes(x=d6, y=d7a))+
  geom_point()+
  geom_smooth(method=lm, se=F)+ #agregar línea de tendencia
  labs(x="Aprobación de matrimonio igualitario", 
       y="Aprobación de adopción")+ #para etiquetar los ejes
  theme_light()

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 781 rows containing non-finite outside the scale range
## (`stat_smooth()`).

## Warning: Removed 781 rows containing missing values or values outside the scale range
## (`geom_point()`).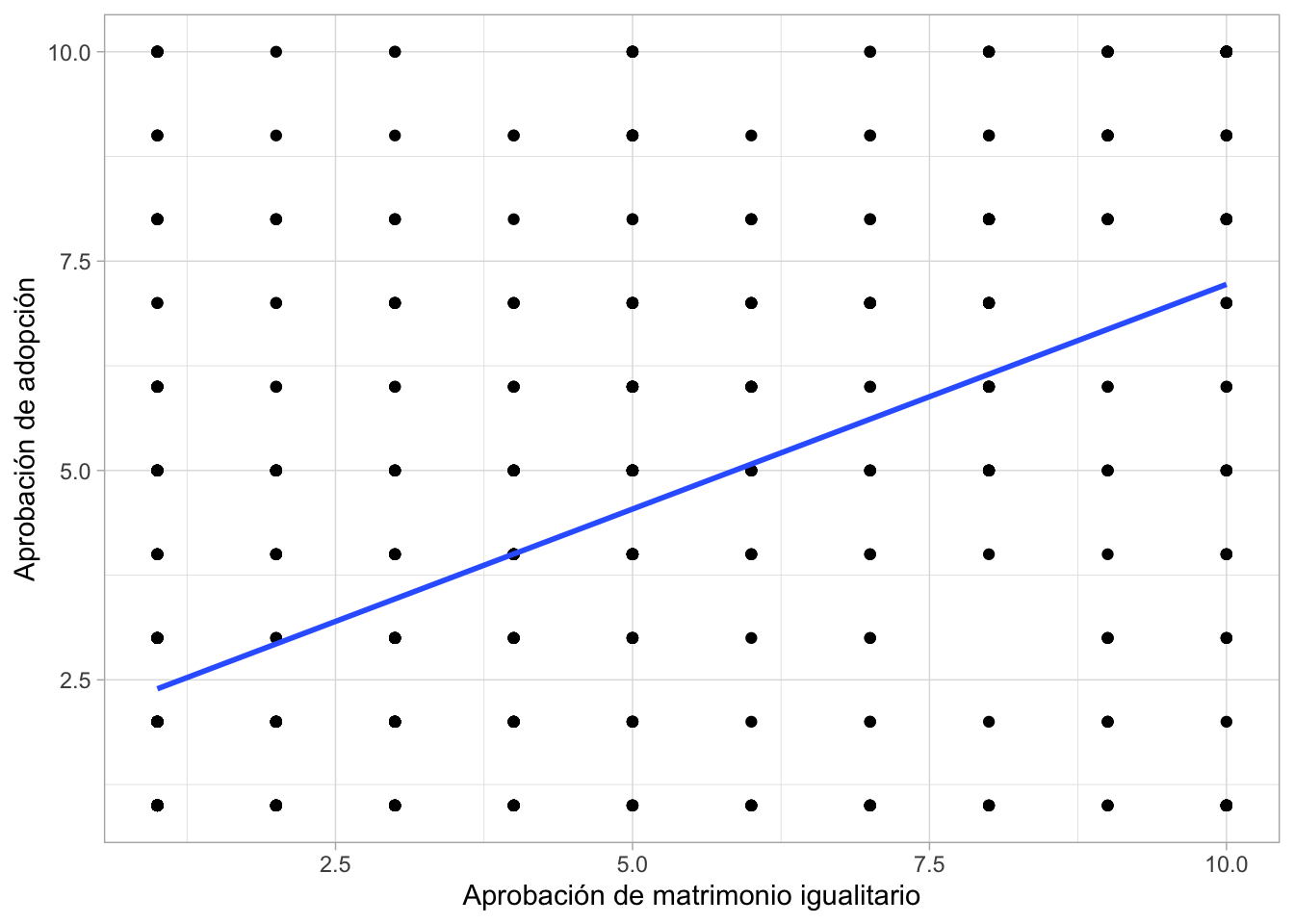

modelo1 = lm(peru23$d7a ~ peru23$d6)
summary(modelo1)

## 
## Call:
## lm(formula = peru23$d7a ~ peru23$d6)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.2226 -1.3931 -0.5396  1.8506  7.6069 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.85649    0.15316   12.12   <2e-16 ***
## peru23$d6    0.53661    0.02952   18.18   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.633 on 752 degrees of freedom
##   (781 observations deleted due to missingness)
## Multiple R-squared:  0.3053, Adjusted R-squared:  0.3044 
## F-statistic: 330.5 on 1 and 752 DF,  p-value: < 2.2e-16

peru23 = peru23 %>%
  mutate(mujer = q1tc_r-1)

modelo2 = lm(peru23$d7a ~ peru23$d6 + peru23$mujer)
summary(modelo2)

## 
## Call:
## lm(formula = peru23$d7a ~ peru23$d6 + peru23$mujer)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.3401 -1.5450 -0.6761  1.7911  7.7294 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.73783    0.17549   9.903   <2e-16 ***
## peru23$d6     0.53279    0.02964  17.975   <2e-16 ***
## peru23$mujer  0.27434    0.19283   1.423    0.155    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.634 on 749 degrees of freedom
##   (783 observations deleted due to missingness)
## Multiple R-squared:  0.3071, Adjusted R-squared:  0.3053 
## F-statistic:   166 on 2 and 749 DF,  p-value: < 2.2e-16