Clase 7

Introducción

La prueba t y la prueba de ANOVA analiza el impacto de una variable independiente categórica en una variable dependiente numérica. El paso que vamos a dar en esta sección es analizar la relación bivariada entre dos variables de factor (o categóricas). Esta evaluación se realiza mediante la prueba de chi-cuadrado.

• Chi-cuadrado:

  • Variable independiente (país) -> Variable dependiente (apoyo a la democracia).

  • Variable independiente (situación económica) -> Variable dependiente (satisfacción con la vida)

  • Variable independiente(nivel educativo) -> Variable dependiente (satisfacción con la democracia)

Tablas de contingencia

Se trata de tablas de doble entrada (como mínimo) para analizar los datos de variables categóricas. Una variable va en las filas y otra en las columnas. Se puede tener los totales por filas o por columnas, que se llaman “distribuciones marginales” y que coinciden con la distribución de la variable individual.

Se puede calcular porcentajes de 3 maneras:

• Porcentajes por filas

• Porcentajes por columnas

• Porcentaje sobre el total

Se recomienda que la variable independiente sea colocada en las columnas y la variable dependiente en las filas. Si se calcula los porcentajes por columnas de esta manera, se podrá comparar las distribuciones condicionales de la variable dependiente por cada grupo de la variable independiente.

En este documento vamos a trabajar con el reporte comparado El Pulso de la Democracia, disponible aquí. Este reporte presenta los principales hallazgos del proyecto del Barómetro de las Américas, organizado por el Proyecto de Opinión Pública en América Latina (LAPOP, por sus siglas en inglés). En este documento se reportan los resultados de la última ronda disponible de 2023.

Pueden descargar los datos de manera libre aquí.](http://datasets.americasbarometer.org/database/login.php).) En este enlace, se pueden registrar o entrar como “Free User”. En el buscador, se puede ingresar el texto “2023”. Ahí se tendrá acceso a las bases de datos completas de la ronda 2021 y de todas las rondas de cada país en versión para STATA. Se descarga la base de datos en formato .dta. Una vez descargada y guardada en el directorio de trabajo, se tiene que leer la base de datos como un objeto dataframe en R. El cuestionario de esta base de datos puede ser visto en este enlace.

library(rio)
peru23 = import("bases/PER_2023_LAPOP_AmericasBarometer_v1.0_w.sav")

Desde la pag. 20 del reporte se hace una evaluación de la democracia en la práctica. En particular, se trabaja con la variable PN4. En general, ¿usted diría que está muy satisfecho(a), satisfecho(a), insatisfecho(a) o muy insatisfecho(a) con la forma en que la democracia funciona en Perú. El reporte se indica que los datos se recodifican en una variable dicotómica. En este documento vamos a trabajar con la variable original. Esta variable es una variable categórica, ordinal o de factor. En el Gráfico 1.14 del reporte se presenta una evaluación de la satisfacción con la democracia por variables demográficas y socioeconómica, como nivel educativo, quintiles de riqueza, lugar de residencia, género o grupos de edad. Es decir, se usa la satisfacción con la democracia como variable dependiente y a cada variable demográficas y socioeconómica como variables independientes.

Por ejemplo, se reporta que entre los hombres, el 42.3% están satisfechos con la democracia, mientras que entre las mujeres, este porcentaje disminuye a 36.9%.

Antes de proceder, tenemos que recodificar las variables, ponerlas en forma de factor y etiquetar.

library(tidyverse)
peru23 = peru23 %>%
  mutate(sexo = factor(q1tc_r, labels=c("Hombre", "Mujer")))

table(peru23$sexo)

## 
## Hombre  Mujer 
##    769    761

Lo mismo para la variable PN4 que se transforma en la variable “satis”.

peru23 = peru23 %>%
  mutate(satis = factor(pn4, labels= c("Muy satisfecho", "Satisfecho", 
                                       "Insatisfecho", "Muy insatisfecho")))

tabla1 = table(peru23$satis)
tabla1

## 
##   Muy satisfecho       Satisfecho     Insatisfecho Muy insatisfecho 
##               58              233              944              280

Para calcular la tabla de satisfacción con la democracia, independiente del género de la persona, se puede calcular los porcentajes de esta variable con el comando prop.table. Se multuplica por 100 para tener el formato de porcentaje.

tabla1 %>%
  prop.table()*100

## 
##   Muy satisfecho       Satisfecho     Insatisfecho Muy insatisfecho 
##         3.828383        15.379538        62.310231        18.481848

Ahora, se puede calcular la tabla de contingencia entre satisfacción y género. El comando table nos brinda las frecuencias absolutas del cruce entre ambas variables. La variable dependiente “satisfacción con la democracia” se ubica en las filas y la variable independiente “sexo” en las columnas. Se verifica que las 58 observaciones que están muy satisfechas con la democracia, se dividen en 27 hombres y 29 mujeres.

tabla2 = table(peru23$satis, peru23$sexo)
tabla2

##                   
##                    Hombre Mujer
##   Muy satisfecho       27    29
##   Satisfecho          132   101
##   Insatisfecho        456   485
##   Muy insatisfecho    148   132

Para calcular las frecuencias relativas, se tiene que usar el comando prop.table. Se agrega la especificación (2) para indicar que se quiere las proporciones sobre las columnas. Se sigue con el comando round para eliminar los decimales innecesarios y finalmente se usa addmargins para verificar la suma de proporciones sobre las columnas.

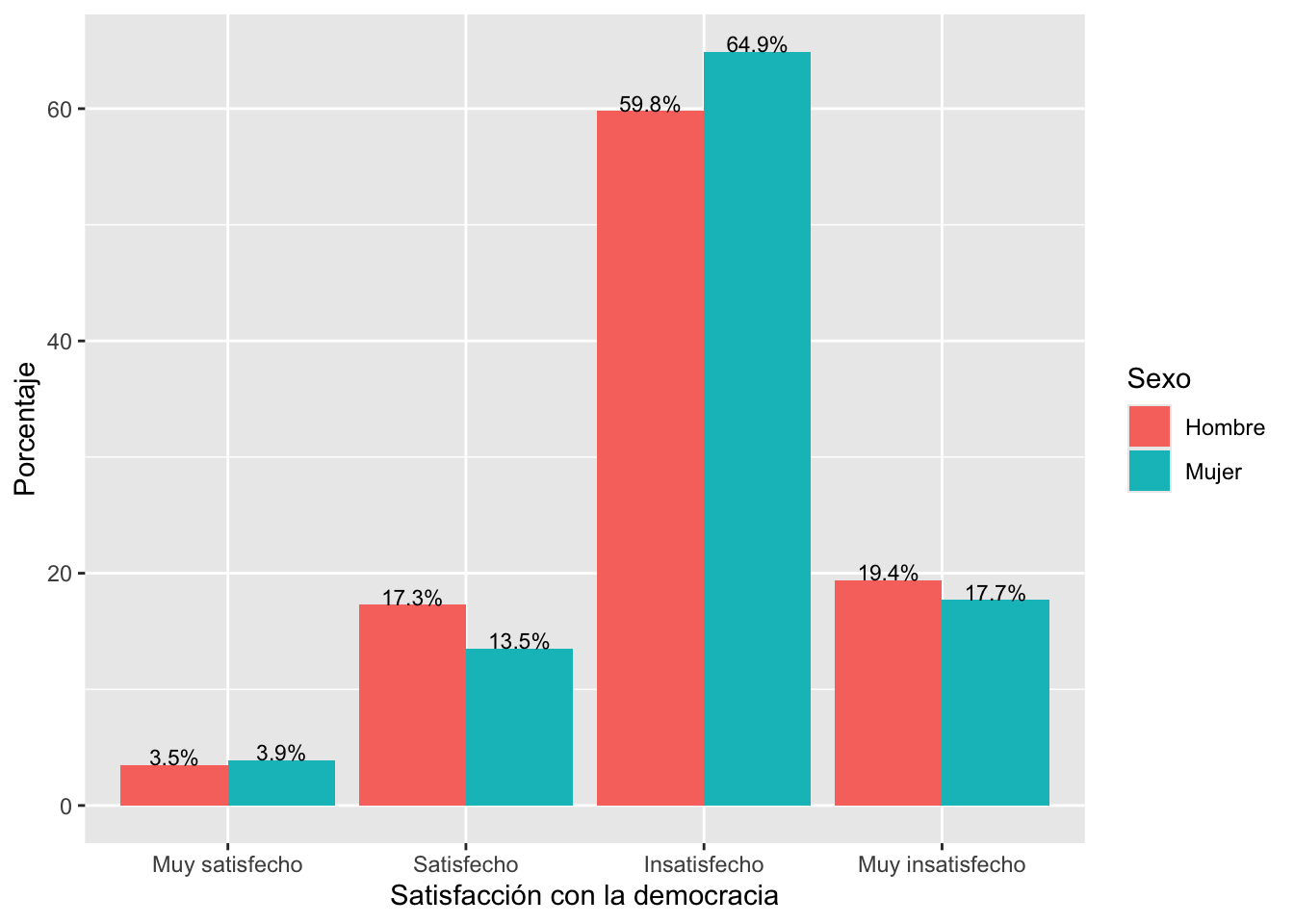
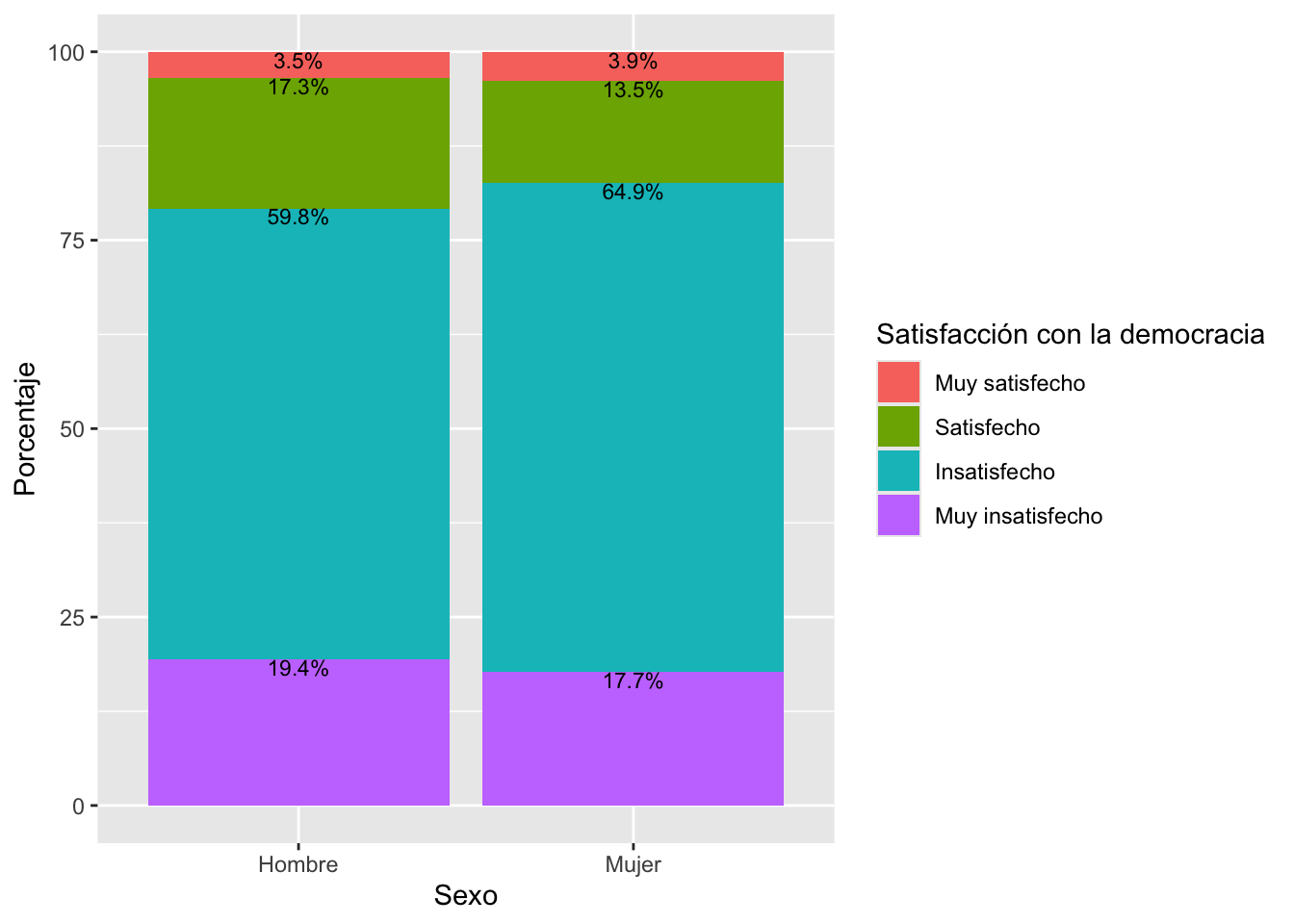
tabla3 = tabla2 %>%
  prop.table(2) %>%
  round(3)*100 
tabla3

##                   
##                    Hombre Mujer
##   Muy satisfecho      3.5   3.9
##   Satisfecho         17.3  13.5
##   Insatisfecho       59.8  64.9
##   Muy insatisfecho   19.4  17.7

En esta tabla se muestra las distribuciones condicionales de satisfacción con la democracia por cada grupo de género. Por ejemplo, el 3.5% de los hombres se encuentras muy satisfechos con la democracia, un porcentaje algo similar al 3.9% de las mujeres. El 17.3% de los hombres se encuentran satisfechos con la democracia, 4 puntos porcentuales por encima que las mujeres.

De esta manera, se pueden comparar los porcentajes por cada categoría de la variable dependiente entre grupos de la variable independiente y, además, se puede comparar con los porcentajes no condicionales de la variable satisfacción con la democracia.

peru23 = peru23 %>%
  mutate(protesta = factor(prot3, labels= c("Sí ha participado", 
                                            "No ha participado")))

tabla4 = table(peru23$protesta, peru23$sexo)
tabla4 = tabla4 %>%
  prop.table(2) %>%
  round(3)*100
tabla4

##                    
##                     Hombre Mujer
##   Sí ha participado   13.3  10.2
##   No ha participado   86.7  89.8

prueba2 = chisq.test(peru23$protesta, peru23$sexo)
prueba2

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  peru23$protesta and peru23$sexo
## X-squared = 3.0967, df = 1, p-value = 0.07845

peru23 = peru23 %>%
  mutate(urbano = factor(ur, labels= c("Urbano", "Rural")))

tabla5 = table(peru23$protesta, peru23$urbano)
tabla5 = tabla5 %>%
  prop.table(2) %>%
  round(3)*100
tabla5

##                    
##                     Urbano Rural
##   Sí ha participado   10.4  16.1
##   No ha participado   89.6  83.9

prueba3 = chisq.test(peru23$protesta, peru23$urbano)
prueba3

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  peru23$protesta and peru23$urbano
## X-squared = 8.1579, df = 1, p-value = 0.004287

Gráficos bivariados categóricos

Para crear un gráfico se tiene que guardar la tabla como un dataframe. Se usa el comando as.data.frame para salvar los porcentajes y poder usarlos con el comando ggplot. Nótese que el dataframe guarda los porcentajes en otro formato.

tabla4 = as.data.frame(tabla3)
tabla4

##               Var1   Var2 Freq
## 1   Muy satisfecho Hombre  3.5
## 2       Satisfecho Hombre 17.3
## 3     Insatisfecho Hombre 59.8
## 4 Muy insatisfecho Hombre 19.4
## 5   Muy satisfecho  Mujer  3.9
## 6       Satisfecho  Mujer 13.5
## 7     Insatisfecho  Mujer 64.9
## 8 Muy insatisfecho  Mujer 17.7

En este caso, como tenemos 4 categorías para satisfacción con la democracia y otras 2 para sexo, un gráfico de barras separadas crearía 8 barras.

library(ggplot2)
ggplot(data=tabla4, aes(x=Var1, y=Freq, fill=Var2))+
  geom_bar(position = "dodge", stat="identity")+
  geom_text(aes(label=paste(Freq, "%", sep="")), 
            position = position_dodge(width = 0.9), 
            vjust=0, size = 3)+
  labs(x="Satisfacción con la democracia", y="Porcentaje", fill="Sexo")

Esta forma de graficar puede complicar la comparación en algunos casos. Por eso, en otros casos, se prefiere el tipo de barras apiladas.

ggplot(data=tabla4, aes(x=Var2, y=Freq, fill=Var1))+
  geom_bar(position="stack", stat="identity")+
  geom_text(aes(label=paste(Freq, "%", sep="")), 
            position = position_stack(), vjust=1, size = 3)+
  labs(x="Sexo", y="Porcentaje", fill="Satisfacción con la democracia")

Independencia y dependencia

Decimos que dos variables categóricas son estadísticamente independientes si las distribuciones condicionales (poblacionales) son idénticas por cada categoría de la variable independiente. Por ejemplo, la siguiente tabla, si mostrara los porcentajes poblacionales condicionales, estos son idénticos entre grupos de la variable independiente. Es decir, independientemente de ser hombre o mujer, las distribución de satisfacción por la democracia es la misma. Ser hombre o mujer no cambia nada las opiniones con respecto a la satisfacción con la democracia.

Satisfacción con la democracia	Hombre	Mujer
Muy satisfecho	3.5%	3.9%
Satisfecho	17.3%	13.5%
Insatisfecho	59.8%	64.9%
Muy insatisfecho	19.4%	17.7%

VI: fuma ———> VD: cáncer de pulmón

	Fuma
Cáncer al pulmón	Fumador	No fumador
Si desarrolla cáncer	10	10
No desarrolla cáncer	90	90
Total	100%	100%

A medida que estos porcentajes difieren más entre sí, hay más probabilidades que ambas variables estén relacionadas. En realidad, a medida que estos porcentajes difieren más de la distribución no condicional de la variable satisfacción con la democracia también habría una mayor probabilidad de que estén relacionadas.

Prueba de independencia de chi-cuadrado

Se basa en la comparación de las frecuencias observadas (las observaciones que se recoge en campo) versus las frecuencias esperadas (las observaciones que debería haber en cada celda de la tabla si las variables fueran independientes). En ese sentido \(H_0: f_e = f_o\) o lo que es lo mismo que las variables son independientes.

Si no hubiera relación entre las variables, tendríamos los mismo porcentajes reproducidos en las distribuciones condicionales.

Col1	Hombres	Mujeres
MS	2.1% de hombres -> #observaciones si no hay relación cuánto es el 2.1% de 1617 = 34 -> #obs si NO hubiera relación Pero, 19 es lo realmente observado (19-34)^2	2.1% de mujeres -> #observaciones si no hay relación cuánto es el 2.1% de 1421 = 29.8 -> #obs si NO hubiera relación Pero, 12 es lo realmente observado (12-29.8)^2
S	18.6%	18.6%
I	61.3%	61.3%
MI	18%	18%
	100%	100%

Prueba estadística

El chi-cuadrado resume qué tan cerca están las frecuencias esperadas de las frecuencias observadas. Mientras más pequeña la distancia en cada celda, menos probabilidades de rechazar la hipótesis nula. Mientras la distancia más grande en cada celda ,más probabilidades de rechazar la hipótesis nula.

\[ \chi^2 = \sum\frac{(f_o-f_e)^2}{f_e} \]

• Si fo=fe en cada celda, entonces χ^2 = 0

• Con el valor de \(\chi^2\) se calcula un p-value, que tiene que ser menor de 0.05 para rechazar la Ho.

• Se requiere que haya al menos 5 observaciones en cada celda

En R se usa el comando chisq.test para calcular el estadístico y el p-value. Esta prueba es mejor guardarla en un objeto nuevo

prueba = chisq.test(peru23$satis, peru23$sexo)

La primera tabla presenta las frecuencias observadas, que es lo que realmente se recoge en campo. La segunda tabla presenta las frecuencias esperadas (si no hubiera relación). Se comprueba los cálculos que se hizo en la tabla anterior (las diferencias son debido a la aproximación decimal).

El estadístico \(\chi^2\) resume las diferencias entre las frecuencias observadas y esperadas en cada celda y las suma de acuerdo a la fórmula.

prueba

## 
##  Pearson's Chi-squared test
## 
## data:  peru23$satis and peru23$sexo
## X-squared = 5.835, df = 3, p-value = 0.1199

La prueba nos da como resultado un p-value = 0.12, por lo que NO se puede rechazar la hipótesis nula y se concluye que no sabemos si existe asociación/relación/dependencia entre las variables.

Tabla cruzada de satisfacción con la democracia según nivel educativo

El Gráfico 1.14 del reporte muestra los datos de satisfacción con la democracia (según la variable recodificada dummy) por niveles educativo. Como segundo ejemplo, aquí vamos a replicar esa relación usando la variable original de tipo factor para Perú 2023.

Vamos a recodificar la variable educación. La variable original “edre” separa los niveles educativos en 7 niveles (del 0 al 6). Los analfabetos son un grupo muy pequeño y podrían causar problemas.

Primero, creamos una variable “educ”, como el factor de “edre”. Luego, se etiqueta.

peru23 = peru23 |>
  mutate(educ = factor(edre, labels=c("Analfabeto", "Primaria incompleta", 
                                      "Primaria completa","Secundaria incompleta",
                                      "Secundaria completa",
                                      "Universitaria o técnica incompleta", 
                                      "Universitaria o técnica completa")))
table(peru23$educ)

## 
##                         Analfabeto                Primaria incompleta 
##                                  8                                 80 
##                  Primaria completa              Secundaria incompleta 
##                                 90                                133 
##                Secundaria completa Universitaria o técnica incompleta 
##                                511                                270 
##   Universitaria o técnica completa 
##                                443

Vamos a crear otra variable de educación “educ2” que junte categorías para que no hayan 7 niveles educativos.

peru23 = peru23 |>
    mutate(educ2= case_when(
    edre == 0 ~ 1,
    edre == 1 ~ 1,
    edre == 2 ~ 1,
    edre == 3 ~ 2,
    edre == 4 ~ 2,
    edre == 5 ~ 3,
    edre == 6 ~ 4,
    ))

peru23 = peru23 |>
  mutate(educ2 = factor(educ2, labels=c("Hasta primaria ", "Hasta secundaria",
                                      "Universitaria o técnica incompleta", 
                                      "Universitaria o técnica completa")))
table(peru23$educ2)

## 
##                    Hasta primaria                    Hasta secundaria 
##                                178                                644 
## Universitaria o técnica incompleta   Universitaria o técnica completa 
##                                270                                443

Con la variable recodificada se puede calcular la tabla cruzada de satisfacción con la democracia según niveles educativos.

tabla4 = table(peru23$satis, peru23$educ2)
tabla4

##                   
##                    Hasta primaria  Hasta secundaria
##   Muy satisfecho                23               25
##   Satisfecho                    20              112
##   Insatisfecho                  88              405
##   Muy insatisfecho              36               94
##                   
##                    Universitaria o técnica incompleta
##   Muy satisfecho                                    3
##   Satisfecho                                       38
##   Insatisfecho                                    180
##   Muy insatisfecho                                 49
##                   
##                    Universitaria o técnica completa
##   Muy satisfecho                                  7
##   Satisfecho                                     63
##   Insatisfecho                                  271
##   Muy insatisfecho                              101

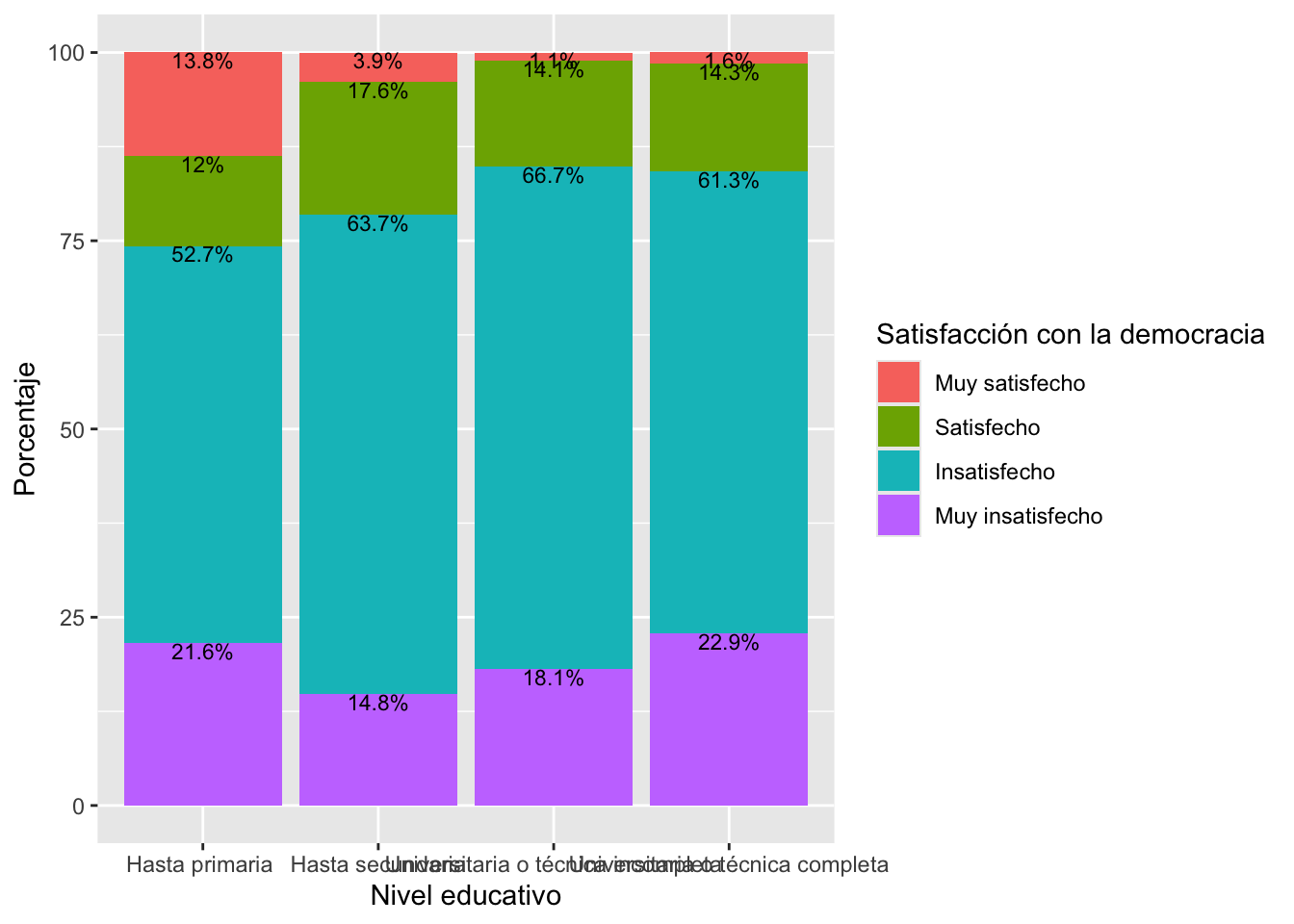
tabla4 = tabla4 |>
  prop.table(2) |>
  round(3)*100
tabla4

##                   
##                    Hasta primaria  Hasta secundaria
##   Muy satisfecho              13.8              3.9
##   Satisfecho                  12.0             17.6
##   Insatisfecho                52.7             63.7
##   Muy insatisfecho            21.6             14.8
##                   
##                    Universitaria o técnica incompleta
##   Muy satisfecho                                  1.1
##   Satisfecho                                     14.1
##   Insatisfecho                                   66.7
##   Muy insatisfecho                               18.1
##                   
##                    Universitaria o técnica completa
##   Muy satisfecho                                1.6
##   Satisfecho                                   14.3
##   Insatisfecho                                 61.3
##   Muy insatisfecho                             22.9

Gráfico bivariado de satisfacción con la democracia según educación

tabla5 = as.data.frame(tabla4)
tabla5

##                Var1                               Var2 Freq
## 1    Muy satisfecho                    Hasta primaria  13.8
## 2        Satisfecho                    Hasta primaria  12.0
## 3      Insatisfecho                    Hasta primaria  52.7
## 4  Muy insatisfecho                    Hasta primaria  21.6
## 5    Muy satisfecho                   Hasta secundaria  3.9
## 6        Satisfecho                   Hasta secundaria 17.6
## 7      Insatisfecho                   Hasta secundaria 63.7
## 8  Muy insatisfecho                   Hasta secundaria 14.8
## 9    Muy satisfecho Universitaria o técnica incompleta  1.1
## 10       Satisfecho Universitaria o técnica incompleta 14.1
## 11     Insatisfecho Universitaria o técnica incompleta 66.7
## 12 Muy insatisfecho Universitaria o técnica incompleta 18.1
## 13   Muy satisfecho   Universitaria o técnica completa  1.6
## 14       Satisfecho   Universitaria o técnica completa 14.3
## 15     Insatisfecho   Universitaria o técnica completa 61.3
## 16 Muy insatisfecho   Universitaria o técnica completa 22.9

ggplot(data=tabla5, aes(x=Var2, y=Freq, fill=Var1))+
  geom_bar(position="stack", stat="identity")+
  geom_text(aes(label=paste(Freq, "%", sep="")), 
            position = position_stack(), vjust=1, size = 3)+
  labs(x="Nivel educativo", y="Porcentaje", 
       fill="Satisfacción con la democracia")

Prueba estadística entre satisfacción con la democracia según educación

Para comprobar la relación entre estas variables, también se puede usar la prueba de independencia de \(\chi^2\). Esta evaluación se guarda en un objeto “prueba2”.

prueba2 = chisq.test(peru23$satis, peru23$educ2)
prueba2

## 
##  Pearson's Chi-squared test
## 
## data:  peru23$satis and peru23$educ2
## X-squared = 71.87, df = 9, p-value = 6.539e-12

prueba2 = chisq.test(peru23$satis, peru23$educ2)
prueba2

## 
##  Pearson's Chi-squared test
## 
## data:  peru23$satis and peru23$educ2
## X-squared = 71.87, df = 9, p-value = 6.539e-12

Con el valor de estadístico se obtiene un p-value menor a 0.05, con lo que se rechaza la hipótesis nula y se afirma que las frecuencias observadas son diferentes de las esperadas, con lo que concluimos que sí existe una relación de dependencia entre las variables. Esto quiere decir que en Perú en 2023 existen diferencias en la satisfacción con la democracia entre diferentes grupos por nivel educativo.