Clase 2: descripción y visualización
Arturo Maldonado
27/08/2024
Caso 1: Apoyo a la democracia en América Latina
Pregunta: ¿existe una erosión del apoyo a la democracia entre los ciudadanos en América Latina?
Leer una base de datos
Usamos la librería rio. Activamos la librería con el
comando library y usamos el comando import
para leer la base de datos (un archivo Excel). Ojo: el nombre del
archivo tiene que estar entre comillas. En este caso, el archivo está
dentro de mi directorio de trabajo, por lo que se le llama con el
nombre. Si no estuviera en el directorio de trabajo se tendría que
especificar la ruta del archivo.
Guardamos esta base de datos en un nuevo objeto (dataframe) llamado apoyoAL. Se sugiere siempre trabajar con nombres cortos de bases de datos y de variables.
library(rio)
apoyoAL = import("apoyoAL.xlsx")Descripción para variables numéricas
Usamos las medidas de tendencia central para describir una variable
numérica. Podemos usar el comando mean para calcular el
promedio de apoyo a la democracia en 2023. Este comando asume que se
tienen datos completos. Como existe un dato perdido, el comando no
corre, y se tiene que añadir la especificación
, na.rm = T.
library(tidyverse)
apoyoAL %>%
summarise(Apoyo2023=mean(apoyo2023, na.rm=T))## Apoyo2023
## 1 58.56522También se puede calcular la mediana, con el comando
median y presentar ambas medidas juntas.
apoyoAL %>%
summarise(Promedio_Apoyo2023=mean(apoyo2023, na.rm=T),
Mediana_Apoyo2023=median(apoyo2023, na.rm=T))## Promedio_Apoyo2023 Mediana_Apoyo2023
## 1 58.56522 57Ahora lo que queremos averiguar es si el apoyo a la democracia ha disminuido, aumentado o permanecido igual entre 2021 y 2023. Para esto, podemos comparar la media del apoyo a la democracia en 2021 con la media en 2023.
apoyoAL |>
summarise(Promedio_Apoyo2021=mean(apoyo2021, na.rm=T),
Promedio_Apoyo2023=mean(apoyo2023, na.rm=T))## Promedio_Apoyo2021 Promedio_Apoyo2023
## 1 61.2 58.56522Según estos resultados, el apoyo a la democracia ha disminuido de 61.2% a 58.6%; es decir, una disminución de 2.6 puntos porcentuales.
Los datos de 2023 incluyen países caribeños (Bahamas, Granada, TyT y Surinám) que no estaban en el gráfico de 2021. Es posible que el menor promedio de apoyo a la democracia en 2023 sea por la incorporación de estos países. Se podría argumentar que si se tuviera los datos de estos países para 2021, quizá no existiría una erosión del apoyo a la democracia.
Una forma de lidiar con esta observación es comparar los resultados 2023 y 2021 solo de los países que tienen datos en ambos años.
Dataframes
Antes de ver cómo eliminar los países, una nota sobre la estructura de una base de datos. El dataframe apoyoAL tiene 24 observaciones (24 filas, en cada una, un país) y 4 variables (4 columnas, en cada una, una variable). Por lo tanto, este dataframe tiene una dimensión [24, 4]. En general, un dataframe tiene dimensión [#filas, #columnas].
Por lo tanto, se puede llamar a los elementos de un dataframe indicando la fila y la columna. Por ejemplo, para llamar al elemento de la primera fila y segunda columna.
apoyoAL[4,2]## [1] "Argentina"También se puede llamar toda una fila. En este caso, la primera fila.
apoyoAL[1,]## pais country apoyo2021 apoyo2023
## 1 UY Uruguay 80 75O la segunda columna
apoyoAL[,2]## [1] "Uruguay" "El Salvador" "Costa Rica"
## [4] "Argentina" "Chile" "Brasil"
## [7] "Guyana" "México" "Ecuador"
## [10] "Nicaragua" "República Dominicana" "Panamá"
## [13] "Bolivia" "Jamaica" "Colombia"
## [16] "Guatemala" "Paraguay" "Perú"
## [19] "Honduras" "Haití" "Bahamas"
## [22] "Granada" "Trinidad y Tobago" "Surinám"Esto nos permite seleccionar filas (países) o columnas (variables) bajo ciertas condiciones. En general, nos interesa más seleccionar filas.
Por ejemplo, si queremos seleccionar los países por encima de la media de apoyo 2023, podemos decir
apoyoAL[apoyoAL$apoyo2023>mean(apoyoAL$apoyo2023, na.rm = T), c(2,3,4)]## country apoyo2021 apoyo2023
## 1 Uruguay 80 75
## 2 El Salvador 73 67
## 3 Costa Rica 71 72
## 4 Argentina 69 68
## 5 Chile 68 70
## 6 Brasil 67 64
## NA <NA> NA NA
## 8 México 63 62
## 11 República Dominicana 62 64
## 12 Panamá 61 62
## 21 Bahamas NA 65
## 22 Granada NA 59En R existe un comando para seleccionar observaciones. Se puede usar
subset para hacer este filtro. Este filtro se puede
almacenar en otro dataframe.
apoyo_mayor_media = subset(apoyoAL, apoyo2023 > mean(apoyo2023, na.rm=T))En R tenemos los siguientes operadores lógicos:
| Operador | Descripción |
|---|---|
| == | es igual a |
| != | es diferente de |
| > | es mayor de |
| < | es menor de |
| >= | es mayor o igual a |
| <= | es menor o igual a |
| & | intersección (Y) |
| | | unión (O) |
Caso 2: Resultados electorales 2016
Pregunta: Algunos politólogos consideran que un partido más institucionalizado es el que es capaz de tener un mayor enraizamiento territorial y, por lo tanto, tener un apoyo electoral relativamente constante a lo largo del territorio. Por el contrario, un partido menos institucionalizado, solo lograría apoyos electorales diferenciados, mayores en algunos territorios y menores en otros.
Siguiendo esta idea, ¿cuál fue el partido mas o menos institucionalizado de acuerdo a los resultados electorales de 2016?
Leer una base de datos
library(rio)
res2016 = import("resultados2016.xlsx")Si se hace doble click en el objeto, se abre la base de datos como una pestaña en la zona de scripts / RMarkdowns. Este objeto dataframe tiene vectores de datos de tipo “caracter” y otros vectores de datos de tipo “numérico”.
Descripción de la heterogeneidad
Usamos las medidas de dispersión para describir una variable
numérica. Podemos usar el comando sd para calcular la
desviación estándar del voto provincial a Fuerza Popular, a Peruanos por
el Kambio y al Frente Amplio en 2016. Este comando asume que se tienen
datos completos. Si existiera un dato perdido, el comando no correría, y
se tendría que añadir la especificación , na.rm = T.
library(dplyr)
library(tidyverse)
res2016 %>%
summarise(sd(fp), sd(ppk), sd(fa))## sd(fp) sd(ppk) sd(fa)
## 1 15.71665 28.89695 17.34935También se puede calcular la media para grupos de observaciones, es decir para filas específicas de una base de datos. Una opción sería agregar un nuevo dataframe con el filtrado de las observaciones. Si no queremos llenarnos de bases de datos parciales, tenemos otras opciones.
Por ejemplo, si quisiéramos saber si la heterogeneidad del voto fue mayor o menor que aquella del voto provincial general de Fuerza Popular, podríamos calcular la desviación estándar del voto provincial solo en las provincias de Lima.
Esto se puede hacer de múltiples maneras. En este curso comenzaremos a usar las funciones del mundo del Tidyverse.
En cualquier caso, se tiene que seleccionar algunas filas de un
dataframe usando operadores lógicos. En nuestro caso vamos a seleccionar
las observaciones, con el comando filter y con la condición
que en el vector o variable “dpto” sean igual a “LIMA”. Ojo, en
mayúsculas, dado que así está en la base de datos y entre comillas
porque es una cadena de caracteres.
res2016 %>%
filter(dpto =="LIMA") %>%
summarise(sd(fp), sd(ppk), sd(fa))## sd(fp) sd(ppk) sd(fa)
## 1 6.853293 6.539157 4.175478Encontramos que en Lima la desviación estándar del voto provincial a Fuerza Popular es mayor que la de otros partidos. También se puede calcular los mismo para el caso de Cusco.
res2016 %>%
filter(dpto =="CUSCO") %>%
summarize(mean(fp, na.rm=T), mean(ppk, na.rm=T), mean(fa, na.rm=T),
sd(fp), sd(ppk), sd(fa))## mean(fp, na.rm = T) mean(ppk, na.rm = T) mean(fa, na.rm = T) sd(fp)
## 1 19.39154 5.583846 55.17385 7.083839
## sd(ppk) sd(fa)
## 1 3.913559 11.03639#Cómo calcularían esta media usando la variable "id"?Tarea
La base de datos también incluye el voto provincial a Fuerza Popular en la elección de 2021.
¿Calcule si el voto promedio de Fuerza Popular ha aumentado o disminuido entre 2011 y 2016?
¿Calcule lo mismo para el departamento de Tumbes?
¿Calcule si Fuerza Popular ha aumento o disminuido su nivel de institucionalización?
Medidas de tendencia central
Moda
Valor mas frecuente de un conjunto de datos
Es apropiada para todo tipo de datos
Se puede observar directamente en una tabla de distribución de frecuencias.
Mediana
- El valor de la observación central de un conjunto de datos ordenados de menor a mayor.

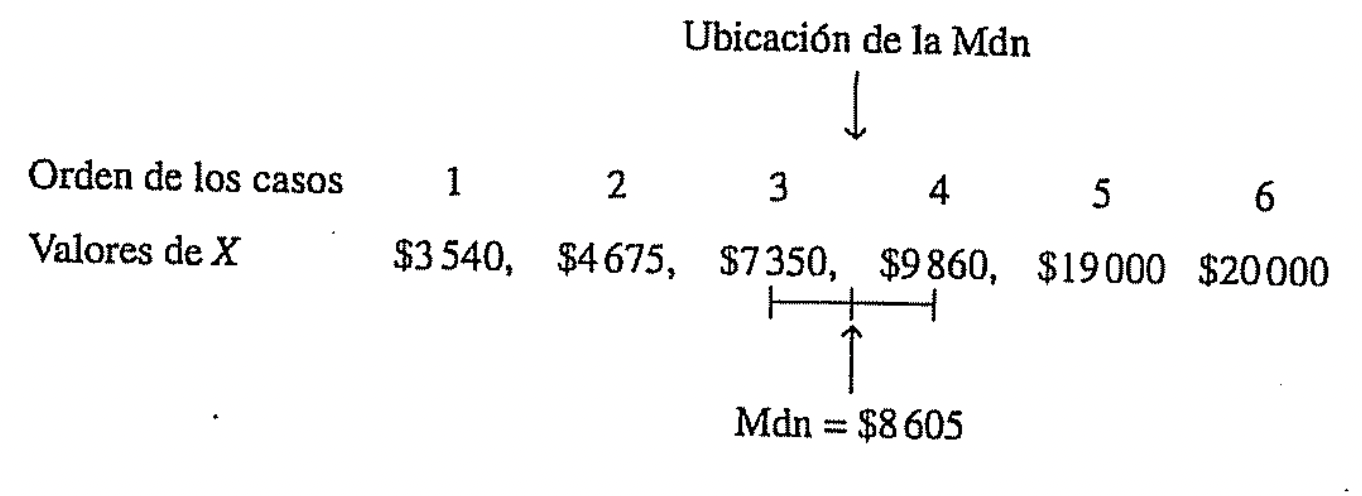
Media
Medida más conocida y “útil”.
Suma del valor de las observaciones dividida entre el número de observaciones
\[ \sum \frac{x_i} {n} = \frac{(x_1 + x_2 +x_3 +...+ x_n)} {n} \]
En una base de datos, se puede calcular la media sumando los valores de una variable (columna de una base de datos) y dividiendo entre el número de casos (# total de filas).
Resumen
| TC | Nominales | Ordinales | Numéricas |
|---|---|---|---|
| Moda | Sí | Sí | Sí |
| Mediana | No | Sí | Sí |
| Media | No | No | Sí |
Moda aplica para cualquier tipo de variable, pero menos útil.
Media aplica solo para variables numéricas, pero más útil.
Medidas de dispersión
Describir la centralidad no es suficiente. Dos distribuciones pueden tener la misma medida de tendencia central, pero diferentes realidades.
Ejemplo: distribución de puntaje en área matemática de prueba PISA aplicada en 2 países pueden tener la misma media, pero diferente variación.
¿Cómo describiría las diferencias entre en los puntajes de la prueba el País A y el País B?
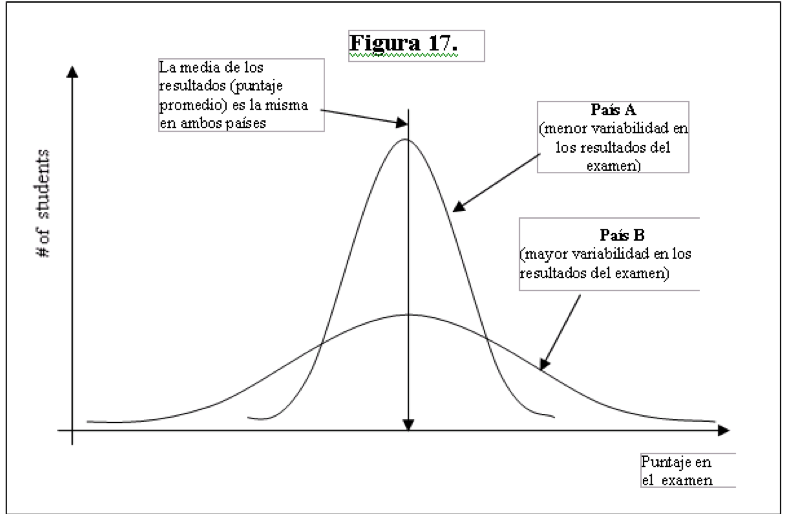
Rango
Diferencia entre el valor máximo y el mínimo. En ejemplo de policías: 259-3 = 256. Es la diferencia entre la comisaría con más efectivos y la comisaría con menor número de efectivos.
No un una medida muy útil.
Rango intercuartil
- Se verá cuando se vean percentiles.
Desviación estándar
Cada observación está a una “distancia” de la media. Esta distancia se llama desviación \((x_i-\bar{x})\)
Observaciones por encima de la media tendrán desviaciones positivas. Observaciones por debajo de la media tendrán desviaciones negativas.
No se puede calcular un promedio de desviaciones porque valores positivos se cancelan con negativos.
Se eleva al cuadrado las observaciones para que todas sean positivas. Se promedian esas desviaciones al cuadrado.
La desviación estándar es la raíz cuadrada de ese promedio de desviaciones al cuadrado.
Se divide entre n-1 por un tema técnico.
\[ \sum \frac{(x_i-\bar{x})^2} {n-1} \]
Para ver un cálculo básico de la desviación estándar en Excel, puede entrar aquí.
- Como se observa en el gráfico anterior, la desviación estándar es más útil cuando se comparar dos distribuciones. Se compara la centralidad y la dispersión de una variable entre dos grupos (o dos distribuciones).