Clase 13

Análisis de regresión como método unificado

Hasta el momento se ha usado el método de regresión lineal para analizar la relación entre dos variables numéricas, tanto la dependiente como las independientes. Este método puede ampliarse y ser usado con una diversidad de tipos de variables independientes, tanto numéricas, como nominales y ordinales.

De esta manera, el método de regresión lineal puede entenderse como un método general, que incluye tanto el análisis de la prueba t como la prueba de ANOVA, dado que ambas usan una variable numérica como variable dependiente.

En resumen, la única condición del análisis de regresión es que la variable dependiente sea numérica, pero las variables independientes pueden ser de diverso tipo.

Regresión lineal como prueba t de diferencia de medias

La prueba t de diferencia de medias se usaba cuando queríamos hacer una inferencia acerca de las medias entre dos grupos. Es decir, para comparar la medida de tendencia central (la media) de una variable dependiente entre (dos) grupos de una variable independiente, que podría ser nominal u ordinal.

Siguiendo con los datos de la elección presidencial de 2016, cargamos la base de datos que hemos estado usando.

library(rio)
data16 = import("bases/datos2016_v3.sav")

Entonces, si queremos saber si existen diferencias estadísticas de la votación a Verónika Mendoza entre los departamentos de la costa y los departamentos que no están en la costa, se puede usar la prueba t de diferencia de medias. Es decir, se quiere comparar la media de votación a Mendoza, una variable cuantitativas, entre grupos de la variable “costa”, variable dicotómica.

Lo primero es ver las medias de cada grupo.

library(dplyr)
data16 %>%
  group_by(costa) %>%
  summarise(Media = mean(Voto_VM_2016_1, na.rm = T))

## # A tibble: 2 × 2
##   costa Media
##   <dbl> <dbl>
## 1     0  29.5
## 2     1  17.9

Para analizar si la diferencia entre 29.5 y 17.9 es significativa, se puede correr una prueba t de diferencias de medias.

t.test(Voto_VM_2016_1 ~ costa, data=data16, var.equal=T)

## 
##  Two Sample t-test
## 
## data:  Voto_VM_2016_1 by costa
## t = 2.1318, df = 23, p-value = 0.04393
## alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
## 95 percent confidence interval:
##   0.3444177 22.9244711
## sample estimates:
## mean in group 0 mean in group 1 
##        29.54000        17.90556

De estos resultados, vemos que se obtiene un p-value de 0.03, que es menor a 0.05. Es decir, la diferencia en el voto a VM entre departamentos de la costa y los que no son de la costa sería significativa.

Para graficar la relación entre ambas variables antes se ha usado un boxplot, que no muestra datos para la inferencia, solo datos descriptivos. También se ha usado un gráfico de barras de error para mostrar las medias de cada grupo con el respectivo intervalo de confianza.

En esta sección, se produce un gráfico de dispersión entre la variable “costa” y “voto a PPK”. Debido a que la variable “costa” es dicotómica, solo tiene valores 0 y 1, por lo que los puntos, que representan a cada departamento, se agrupan en dos líneas verticales.

library(ggplot2)
ggplot(data16, aes(x=costa, y=Voto_VM_2016_1))+
  geom_point()+
  geom_smooth(method=lm, se=F)+ #agregar línea de tendencia
  geom_text(data=data16, aes(label=Dpto), 
            cex=2, nudge_y = 1.1, check_overlap = T)+ #Pata etiquetar los puntos, darles un tamaño, ubicación y prevenir que se sobrepongan
  labs(x="Costa", 
       y="Voto a VM (1era vuelta)")+ #para etiquetar los ejes
  theme_light()

## `geom_smooth()` using formula =
## 'y ~ x'

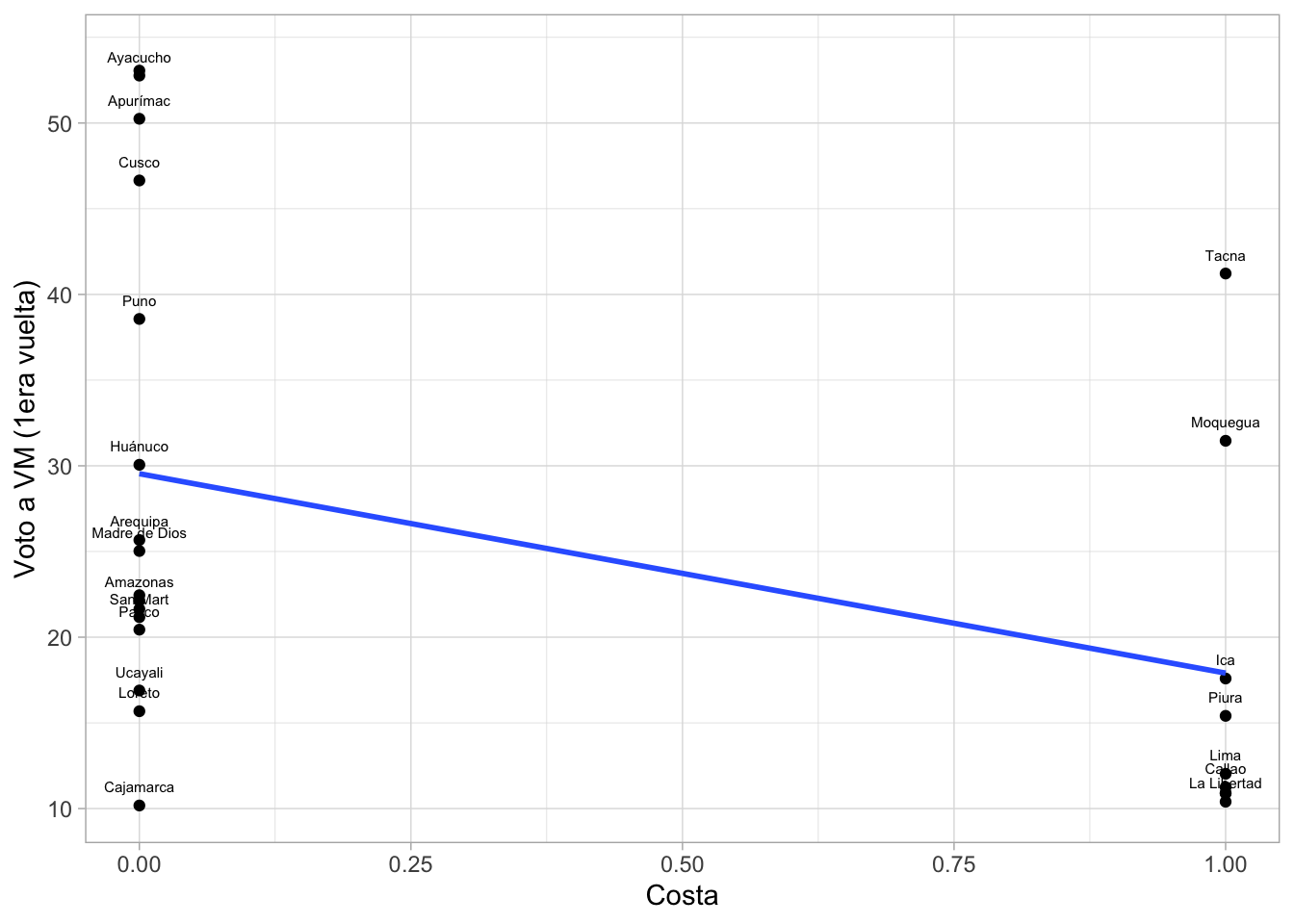
En este gráfico también se puede pensar en una mejor recta de predicción, que reduce la distancia de los puntos a la recta. Esta recta atraviesa por la media de cada grupo.

Por lo tanto, un modelo de regresión que use el voto a VM en primera vuelta en 2016 como variable dependiente y la variable dicotómica “costa” como variable independiente nos daría los datos para la construcción de esta recta de aproximación.

modelo1 = lm(data16$Voto_VM_2016_1 ~ data16$costa)
summary(modelo1)

## 
## Call:
## lm(formula = data16$Voto_VM_2016_1 ~ data16$costa)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -19.360  -7.506  -5.876   9.030  23.520 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    29.540      3.275   9.021 5.15e-09 ***
## data16$costa  -11.634      5.458  -2.132   0.0439 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 13.1 on 23 degrees of freedom
## Multiple R-squared:  0.165,  Adjusted R-squared:  0.1287 
## F-statistic: 4.544 on 1 and 23 DF,  p-value: 0.04393

modelo2 = lm(data16$Voto_VM_2016_1 ~ data16$costa + data16$Analfabetismo_2014)
summary(modelo2)

## 
## Call:
## lm(formula = data16$Voto_VM_2016_1 ~ data16$costa + data16$Analfabetismo_2014)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -26.042  -6.343  -1.668   6.964  26.004 
## 
## Coefficients:
##                           Estimate Std. Error t value Pr(>|t|)   
## (Intercept)                 9.9971     7.0373   1.421  0.16945   
## data16$costa               -0.8333     5.8893  -0.141  0.88877   
## data16$Analfabetismo_2014   2.0173     0.6659   3.030  0.00616 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.25 on 22 degrees of freedom
## Multiple R-squared:  0.4108, Adjusted R-squared:  0.3572 
## F-statistic: 7.669 on 2 and 22 DF,  p-value: 0.002971

Los resultados indican que la recta es \(\hat{Y} = 29.5 - 11.6*X\). Esta recta tiene el valor de 29.5 cuando X=0. Es decir, para los departamentos que no son de la costa, el promedio de voto a VM es 29.5, tal cual encontramos de manera descriptiva. Cuando X=1, el promedio de voto a VM es 29.5 - 11.6 = 17.9, que es el promedio del voto para los departamentos de la costa, el mismo valor que encontramos de manera descriptiva.

Es decir la recta de aproximación pasa por el promedio del voto a VM para los departamentos que no son de la costa y para los que sí son de la costa.

El modelo de regresión no solo replica los datos, sino también replica la prueba de significancia. La hipótesis nula que se evalúa aquí es: \(\mu_{costa} - \mu_{no costa}\).

El estadístico de la prueba t es -2.13 y un p-value de 0.044. Estos datos también se encuentran en la línea de la variable independiente.

Regresión lineal para variables factor

Si quisiéremos evaluar las diferencias en el voto a Fujimori en 2016 entre las 3 regiones: costa, sierra y selva, podríamos usar una variable dependiente numérica y una variable independiente nominal con 3 categorías.

Lo primero es ver las medias del voto a Fujimori para cada grupo.

tabla1 = data16 %>%
  group_by(region) %>%
  summarise(Media = mean(Voto_KF_2016_1, na.rm = T))
tabla1

## # A tibble: 3 × 2
##   region Media
##    <dbl> <dbl>
## 1      1  42.8
## 2      2  31.3
## 3      3  44.8

Para evaluar estas medias mediante el análisis de regresión, se tiene que crear variables dummy por cada grupo de la variable “region”. Es decir, 3 variables: “costa”, “sierra” y “selva”, En el modelo de regresión, sin embargo, solo se debe incluir 2 de esas variables dummy.

modelo2 = lm(data16$Voto_KF_2016_1 ~  data16$costa + data16$sierra+ data16$Analfabetismo_2014)
summary(modelo2)

## 
## Call:
## lm(formula = data16$Voto_KF_2016_1 ~ data16$costa + data16$sierra + 
##     data16$Analfabetismo_2014)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -21.7582  -5.8871  -0.3482   6.6278  21.7204 
## 
## Coefficients:
##                            Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                44.83973    6.57127   6.824 9.55e-07 ***
## data16$costa               -2.04553    5.86485  -0.349   0.7307    
## data16$sierra             -13.53433    5.73836  -2.359   0.0281 *  
## data16$Analfabetismo_2014   0.00134    0.65773   0.002   0.9984    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.32 on 21 degrees of freedom
## Multiple R-squared:  0.2921, Adjusted R-squared:  0.1909 
## F-statistic: 2.888 on 3 and 21 DF,  p-value: 0.05971

Se excluye la tercera variable dummy debido a que los resultados para este grupo se encuentran en el intercepto en el análisis de regresión. Es decir, cuando costa=0 y sierra=0, el voto promedio a Fujimori es 44.85, mismo valor que se encontró en el análisis descriptivo. Cuando costa=1 y sierra=0, el voto promedio a Fujimori es 44.85-2.05 = 42.8, mismo valor que se encontró en el análisis descriptivo. Finalmente, cuando costa=0 y sierra=1, el voto promedio a Fujimori es 44.85-13.53=31.32, mismo valor que se encontró en el análisis descriptivo.

Vemos que los coeficientes de las 2 variables dummy son las diferencias entre los grupos. Los valores de 2.05 y 13.53 son los mismos que se evaluaron en el test de Tukey.

Conclusión

Hemos comenzado la explicación del análisis de regresión como una forma para evaluar la relación entre dos variables numéricas. En esta sección hemos expandido esta idea y hemos visto que el método de regresión se puede usar con variables independientes de tipo categórico, ya sea nominal u ordinal. El único requisito es que la variable dependiente sea numérica.

De esta manera, el modelo de regresión se puede expresar

\[ \hat{Y} = \hat{\alpha} + \hat{\beta_1}*X_1+\hat{\beta_2}*X_2+\hat{\beta_3}*X_3+...+\hat{\beta_n}*X_n \]

Los requisitos son:

• Y es una variable numérica

• Xs pueden ser numéricas o categóricas. Si es categórica, se debe incluir como dummy o serie de variables dummy

• El número de variables independientes no puede ser mayor que el número de observaciones menos 1 (N-1).

En este curso se ha presentado el análisis de regresión lineal como técnica para evaluar la relación bivariada y para evaluar la relación multivariada. Con la técnica de regresión multivariada se puede analizar:

• La validez del modelo.

• La relación de cada predictor con la variable dependiente.

• La dirección de la relación entre cada predictor y la variable dependiente.

• La fuerza del modelo.

• La predicción del modelo para diferentes valores de los predictores.

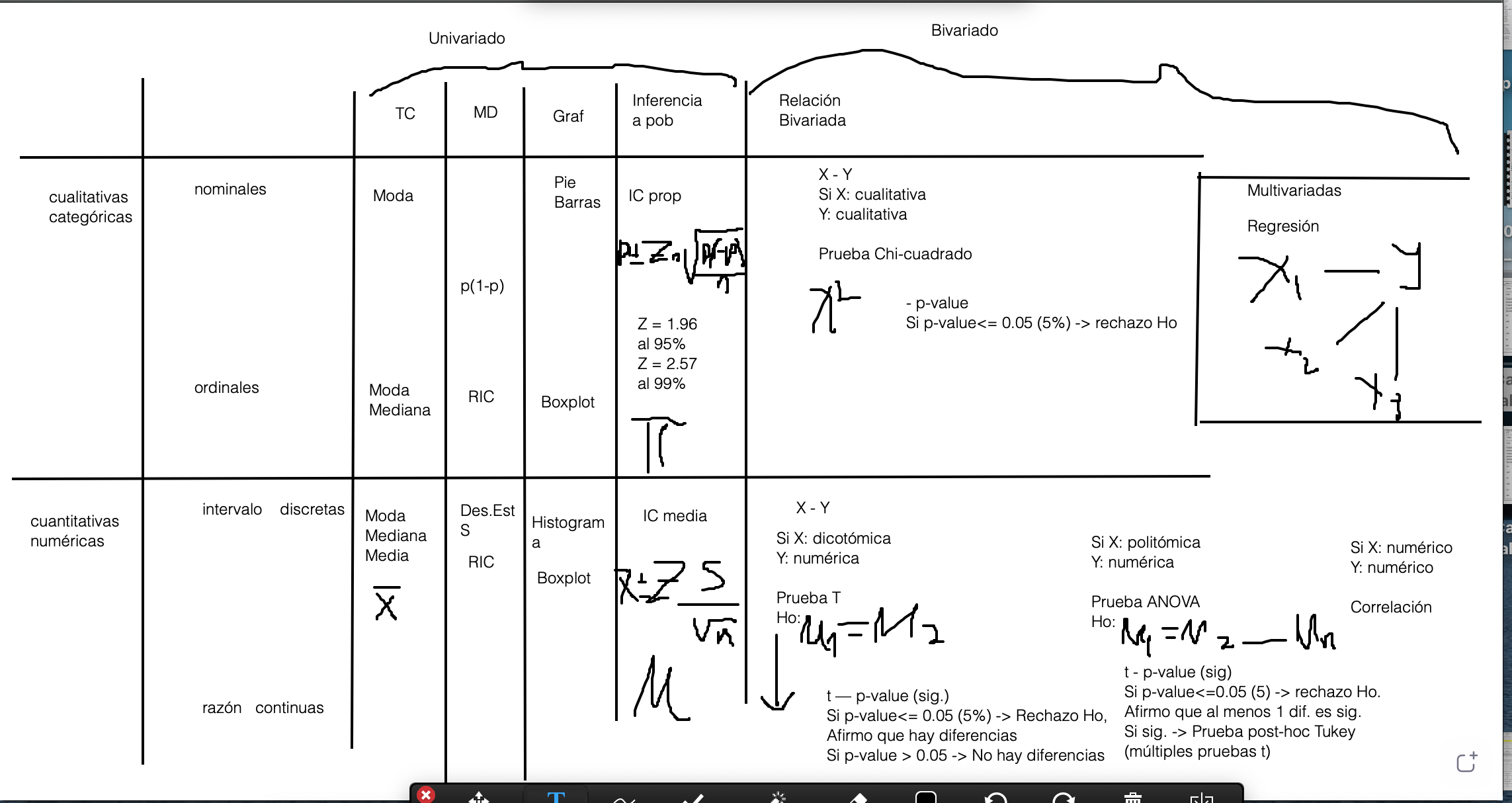
Resumen

En esta sección presentamos un mapa de temas que hemos visto a lo largo de todo el semestre. Como se ve en el esquema, las herramientas que hemos visto en el curso dependen de un punto de partida inicial, que es la distinción entre tipos de variables: cualitativas o categóricas y cuantitativas o numéricas. Dependiendo de esta categorización, se desprende el tipo de análisis descriptivo, tanto de la tendencia central, como de la dispersión, así como las formas de graficar estas variables.

Como paso previo a la inferencia, se construyeron intervalos de confianza de la media (variables cuantitavitas) o de proporciones (variables cualitativas). Se analizó que se podían construir intervalos de confianza de medias o proporciones para grupos. Este es el primer paso de la inferencia. Se evaluó si los intervalos de confianza se traslapaban o no. Esto daba paso al análisis bivariado en la segunda parte del curso.

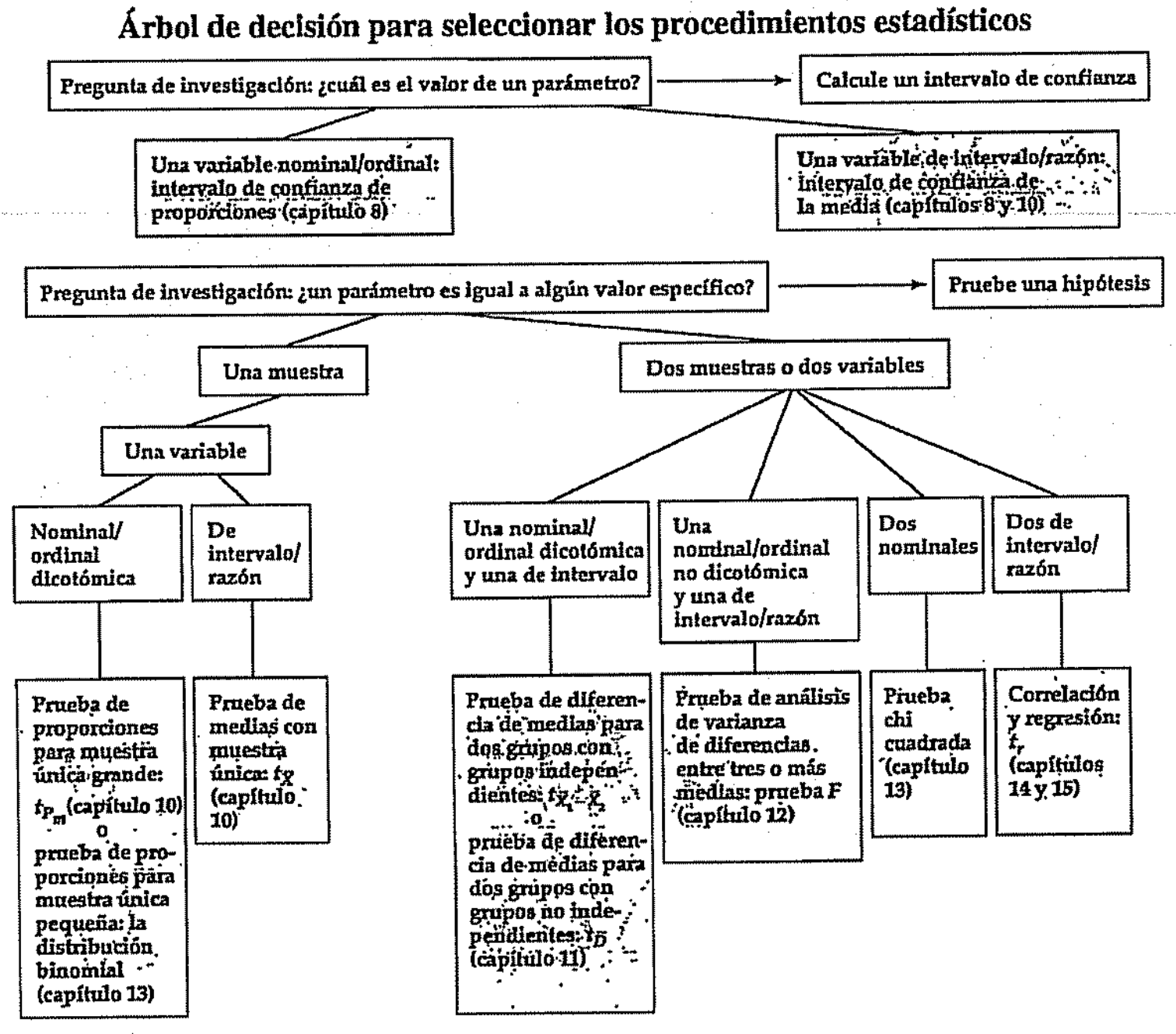
En el libro de Ritchey se muestra este árbol de decisión. La rama derecha de “Dos muestras o dos variables” muestra el resumen de la segunda parte de este curso. Esta segunda parte ha estado dedicada a la inferencia en el análisis bivariado. Como hemos avanzado en este curso, se ha presentado la prueba de inferencia t, la prueba F de ANOVA, la prueba de chi-cuadrado y la regresión bivariada. Luego, se dio el paso al análisis multivariado.

Finalmente, el objetivo de este curso es presentar herramientas iniciales para el análisis de datos sociales. Se espera que luego de este curso los alumnos sean consumidores o productores capaces de estadística. Como consumidores, los alumnos van a estar expuestos a literatura especializada que use métodos estadísticos. Las herramientas vistas en este curso permitirían que los alumnos puedan evaluar estos artículos y los hallazgos de manera crítica.

Como productores, se espera que los alumnos utilicen evidencia numérica y análisis estadístico en sus trabajos de cursos y en sus tesis de pregrado. Ya sea para presentar análisis descriptivo o para realizar análisis inferencial, los alumnos deberían estar en la capacidad de recoger datos numéricos y trabajar con estos usando técnicas vistas en este curso. Es completamente válido que los alumnos usen otros métodos, por ejemplo cualitativos, pero si este curso y el siguiente logran que algunos de ustedes se “atrevan” a usar métodos cuantitativos, ese será el mayor logro de este curso. Gracias!!!