Clase 7

Introducción

Hasta el momento se ha visto la prueba t para comparar medias de solo 2 grupos. En esta sección veremos cómo expandir la comparación para varias medias usando otra prueba de inferencia. Es decir, se busca analizar la relación entre una variable dependiente cuantitativa (o numérica) y una variable independiente categórica (o de factor).

La media de la variable dependiente es comparada para cada grupo de la variable independiente categórica, típicamente una variable nominal. Por ejemplo:

• Ingresos entre grupos étnicos.

• CRAEST entre alumnos de especialidades de Ciencias Sociales.

• Posición ideológica entre simpatizantes de diferentes partidos.

Para poder hacer estas comparaciones entre varios grupos vamos a usar el test del ANOVA

Test de ANOVA

El test de ANOVA sirve para comparar la media de una variable dependiente numérica entre grupos de una variable de tipo factor (con más de 2 grupos).

Este test parte teóricamente de la distribución general de la variable numérica, la que tiene una media poblacional \(\mu\), y compara esta media poblacional general, con las medias poblacionales de la variable numérica por cada grupo de la variable de factor con n grupos, \(\mu_1...\mu_2...\mu_3...\mu_n\).

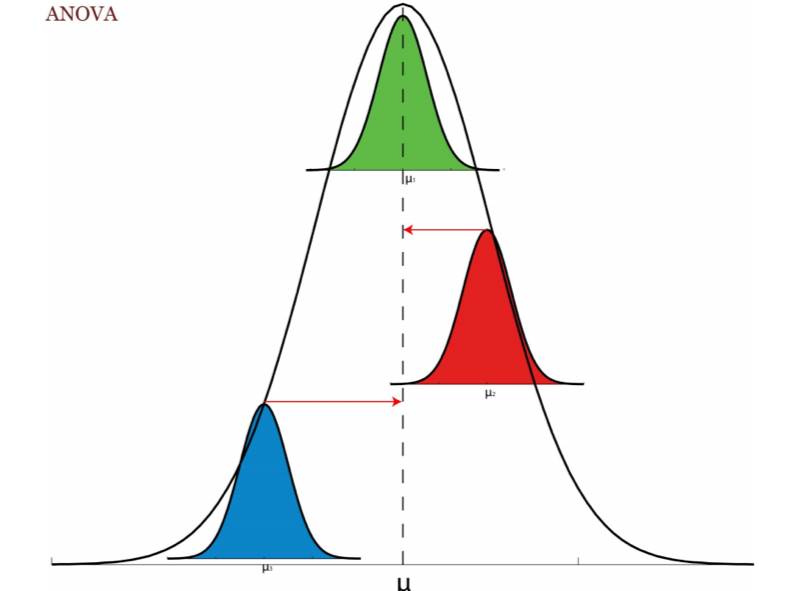
Esta prueba se basa en la distribución F y propone la siguiente hipótesis nula para la comparación de una variable numérica X entre n grupos de la variable de factor.

\[ H0: \mu_{x1} = \mu_{x2} = \mu_{x1} =...= \mu_{xn} \]

La hipótesis alternativa que propone es que al menos una media poblacional de un grupo es diferente. Es decir, si se rechaza la H0, quizá todas las medias poblacionales entre grupos sean distintas, quizá algunas o quizá solo una difiere de las otras.

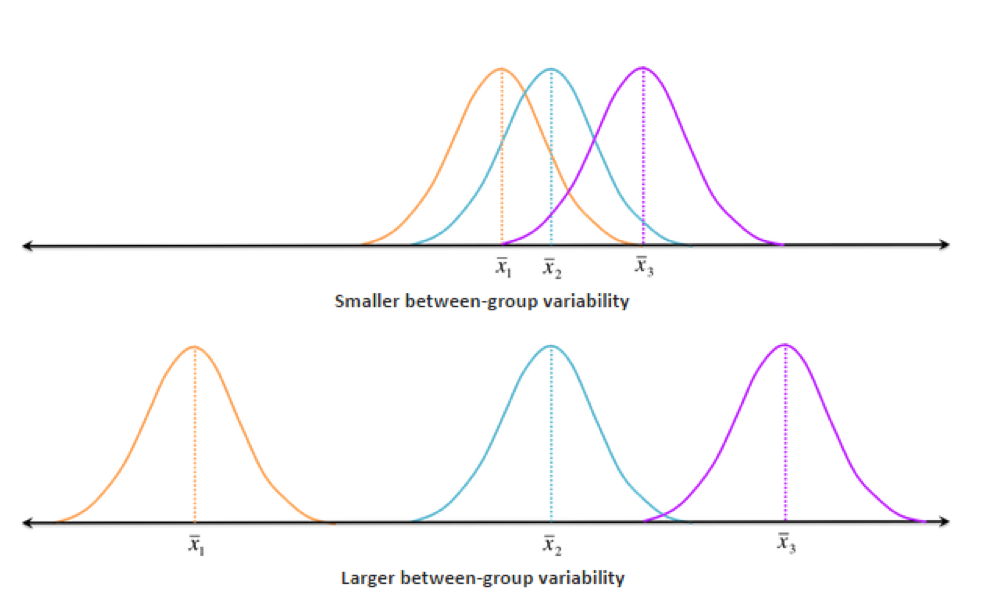
Esta prueba se basa en una comparación entre la variabilidad entre (between) y la variabilidad intra (within).

Variabilidad entre

• La variabilidad entre se refiere a la comparación de la media muestral grupal \(\overline{X}_1\) y la media general \(\overline{X}\).

• Se entiende como un promedio ponderado de las distancias \(\overline{X_g}-\overline{X}\).

• Para evitar que sea una distancia negativa se eleva al cuadrado \((\overline{X_g}-\overline{X})^2\).

• Se pondera por el número de observaciones de cada grupo \(n_g*(\overline{X_g}-\overline{X})^2\).

• Se suma estas cantidades de cada grupo: \(\sum n_g*(\overline{X_g}-\overline{X})^2\).

• Esa suma se divide entre los grados de libertad g-1 (número de grupos -1).

Variabilidad intra

• Es la variabilidad entre las observaciones de cada grupo con su media grupal.

• Se entiende como el cálculo de la desviación estándar en cada grupo.

• Se calcula \(\sum (X_i-\overline{X_g})^2\) en cada grupo. Estas sumatorias se suman.

• Esa suma total se divide entre los grados de libertad N-g (total de observaciones - número de grupos).

Estadístico de la prueba F

• Se calcula como F = estimado de la variabilidad entre / estimado de la variabilidad intra

El estadístico F se hace grande cuando: hay mayor variabilidad entre y/o menos variabilidad intra.

El estadístico F se hace pequeño cuando: hay menor variabilidad entre y/o mayor variabilidad intra.

A medida que el estadístico F es más grande, se ubica más en la cola de la distribución, por lo que el p-value será menor, con los que se tendría una mayor evidencia en contra de la H0 sobre la igualdad de medias poblacionales.

Por lo tanto se concluiría que al menos una de las medias grupales sería significativamente diferente de las otras medias grupales. El tema es que la prueba de ANOVA no llega hasta ahí, no nos indica qué medias son diferentes. Para saber qué media(s) es(son) diferente(s) se tiene que hacer un test posterior.

Post hoc: Test de Tukey

Este test sirve para analizar qué diferencias entre grupos son significativas. Es decir, reporta todos los emparejamientos posibles entre grupos y en cada pareja calcula una prueba t de diferencia de medias y la reporta.

Ejemplo 1 para una variable numérica entre 2+ grupos: ENDO

library(rio)
endo2020 = import("bases/ENDO_REMOTO_2020.dta")

Si queremos evaluar si existen diferencias entre el número promedio de alumnos con los que trabaja un profesor entre tipos de profesores (nombrados, contratados con concurso o contratados con otra modalidad), se puede usar ANOVA.

Primero se tiene que factorizar la variable tipo de profesor (P1_7).

library(dplyr)
library(tidyverse)
endo2020 = endo2020 %>%
  mutate(tipo = factor(P1_7, labels=c("Nombrado", "Contratado por concurso",
                                      "Contratado por otra modalidad")))

alumxtipo = endo2020 %>% 
  group_by(tipo) %>%
  summarize(media = mean(P1_6, na.rm = T), desv = sd(P1_6, na.rm = T))
alumxtipo

## # A tibble: 4 × 3
##   tipo                          media  desv
##   <fct>                         <dbl> <dbl>
## 1 Nombrado                       36.9  48.0
## 2 Contratado por concurso        43.7  53.6
## 3 Contratado por otra modalidad  50.6  66.1
## 4 <NA>                          NaN    NA

alumxtipo = alumxtipo[-4, ]

Para tener una descripción completa entre los 3 grupos, también se puede usar:

library(lsr)
ICalumxtipo = endo2020 %>%
  group_by(tipo) %>%
  summarise(media = mean(P1_6, na.rm=T),
            liminf = ciMean(P1_6, na.rm=T)[1],
            limsup = ciMean(P1_6, na.rm=T)[2]
            )
ICalumxtipo

## # A tibble: 4 × 4
##   tipo                          media liminf limsup
##   <fct>                         <dbl>  <dbl>  <dbl>
## 1 Nombrado                       36.9   36.0   37.8
## 2 Contratado por concurso        43.7   42.5   44.8
## 3 Contratado por otra modalidad  50.6   37.5   63.8
## 4 <NA>                          NaN     NA     NA

ICalumxtipo = ICalumxtipo[-4, ]

¿Qué conclusiones “informales” se pueden sacar del gráfico?

library(ggplot2)
graf1 = ggplot(ICalumxtipo, aes(x=tipo, y=media))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=paste(round(media, 1))), vjust=-1, size=3)+
  xlab("Tipo del contrato") + ylab("Alumnos atendidos")+
  ylim(0, 80)
graf1

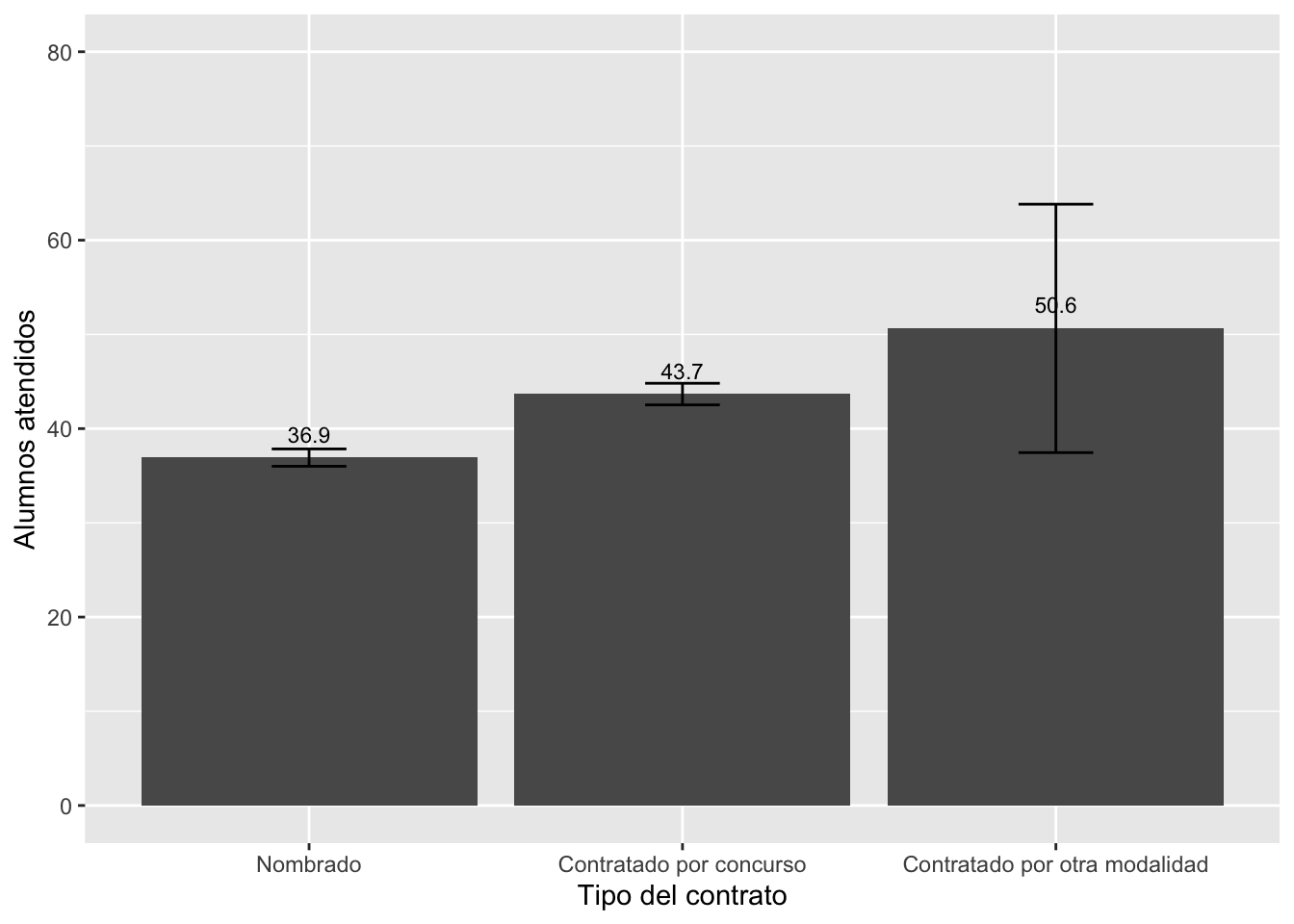
Esta observación visual se tiene que confirmar con la prueba de ANOVA. Para esto se usa el comando aov para crear un objeto “anova1” que luego se describe con summary.

anova1 = aov(endo2020$P1_6~endo2020$tipo)
summary(anova1)

##                  Df   Sum Sq Mean Sq F value Pr(>F)    
## endo2020$tipo     2   223104  111552   43.48 <2e-16 ***
## Residuals     18947 48614075    2566                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 9266 observations deleted due to missingness

Con la prueba de ANOVA y dado que el p-value es menor a 0.05, se puede rechazar la H0. Es decir, se afirma la Ha de que al menos una de las diferencias es significativa. ANOVA no nos indica cuál es la(s) diferencia(s) significativa(s).

Para evaluar las diferencias, se corre la prueba de Tukey para analizar cada emparejamiento. Esto se hace con el comando TukeyHSD en el que se inserta el objeto “anova1” y con el cual se crea un objeto “compara”.

compara = TukeyHSD(anova1)
compara

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = endo2020$P1_6 ~ endo2020$tipo)
## 
## $`endo2020$tipo`
##                                                            diff       lwr
## Contratado por concurso-Nombrado                       6.743547  5.003923
## Contratado por otra modalidad-Nombrado                13.713640  1.724766
## Contratado por otra modalidad-Contratado por concurso  6.970093 -5.032398
##                                                             upr     p adj
## Contratado por concurso-Nombrado                       8.483171 0.0000000
## Contratado por otra modalidad-Nombrado                25.702515 0.0200876
## Contratado por otra modalidad-Contratado por concurso 18.972585 0.3615009

Se observa que los resultados comprueban las observaciones del gráfico. Cada emparejamiento tiene un valor de la diferencia de medias “diff”, un límite inferior “lwr” y límite superior “upr” del intervalo de confianza de esa diferencia y un p-value “p adj”. Este último valor es el que se evalúa para saber si el emparejamiento tiene una diferencia estadísticamente significativa. Se observa que el emparejamiento “Contratado por concurso-Nombrado” tiene un p-value muy pequeño (no es cero, solo faltan decimales), por lo que podemos rechazar la Ho y afirmar que sí existen diferencias en el número de alumnos con los que trabajan estos tipo de profesores.

El emparejamiento entre “Contratado por otra modalidad-Nombrado” tiene un p-value de 0.02, que es menor que 0.05, por lo que concluimos que también existen diferencias en el número de alumnos promedio con el que trabajan estos tipos de profesores.

El emparejamiento “Contratado por otra modalidad-Contratado por concurso” tiene un p-value = 0.36 que es mayor que 0.05, por lo que no se puede concluir que haya diferencias en el promedio de alumnos con los que trabajan estos tipos de profesores.

Este gráfico se puede reproducir con la librería ggplot. Para esto, primero, se tiene que transformar el objeto “compara” (que es una lista) en un dataframe, con el comando as.data.frame y se crea un nuevo objeto “compara.df”, que tiene los valores que requerimos para graficar, excepto que el nombre de las comparaciones esta como nombre de las filas y no como variable. Para incluir las comparaciones como una variable se usa el comando rownames y se crea una nueva columna compara.df$compara.

compara.df = as.data.frame(compara[1])
compara.df$compara = rownames(compara.df)

Con este dataframe, podemos usar la librería ggplot para graficar los intervalos de confianza de las diferencias de medias. Aquellos emparejamientos cuyas líneas no crucen la línea vertical del cero, se puede decir que hay diferencias estadísticamente significativas.

graf2 = ggplot(compara.df, aes(x=compara, y=endo2020.tipo.diff))+
  geom_errorbar(aes(ymin=endo2020.tipo.lwr, ymax=endo2020.tipo.upr), width=0.2)+
  geom_text(aes(label=paste(round(endo2020.tipo.diff, 1))), vjust=-1, size=3)+
  xlab("Comparación") + ylab("Diferencia")+
  ylim(-10, 40) +
  coord_flip() +
  geom_hline(yintercept = 0, color = "red", linetype="dotted") +
  theme_classic()
graf2

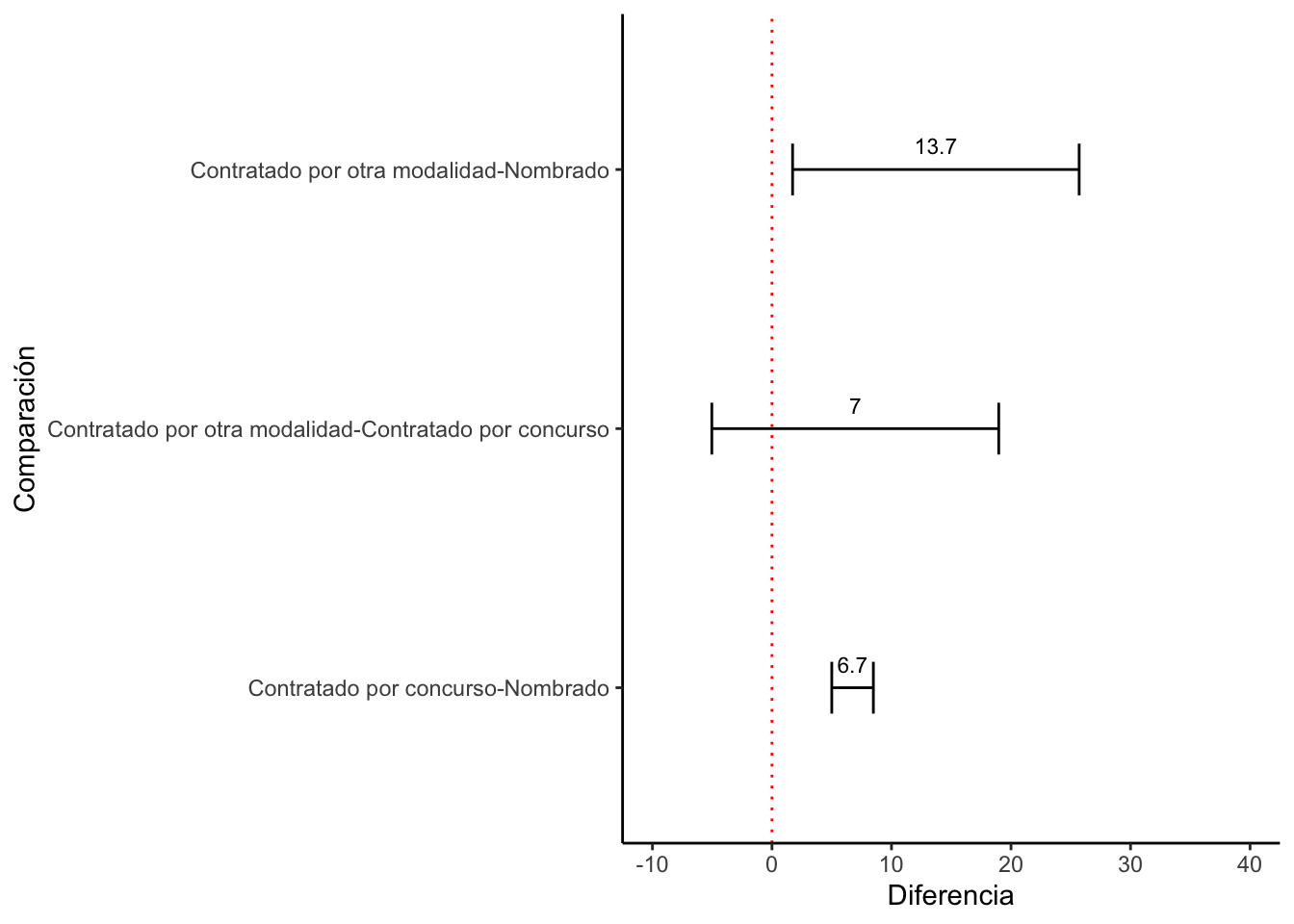
NOTA: Hay ocasiones como esta en que la prueba de ANOVA indica que existe un emparejamiento con una diferencia significativa, y luego, cuando se evalúan los emparejamientos, no se observa esa diferencia. Eso es debido a que cada emparejamiento de evalúa mediante la prueba t de manera autónoma.