Clase 11 y 12

Introducción

El tema de la semana es la correlación y a la regresión lineal simple. Este es un método para analizar la relación entre dos variables cuantitativas: una dependiente y una independiente.

Recordemos que el método del chi-cuadrado se trataba de analizar la relación entre dos variables cualitativas. La prueba t y ANOVA tienen una variable dependiente cuantitativa y una variable independiente cualitativa. La correlación es una extensión de esta serie de relaciones. El método de regresión lineal es un método generalizado, que, luego veremos, incluye a la prueba t y a ANOVA.

La correlación se trata de la evaluación del cambio sistemático en las puntuaciones de dos variables numéricas (discretas o continuas, de intervalo o de razón).

Con el método de la regresión lineal se puede responder las siguientes preguntas:

• Analizar si hay una asociación entre las variables mediante un test de independencia estadística.

• Analizar la dirección de la asociación (directa o inversa).

• Evaluar la fuerza de la asociación usando una medida de asociación llamada correlación de Pearson.

• Estimar una ecuación de regresión que “predice” los valores de la variable dependiente para valores de la variable independiente.

Espacio cartesiano

Se trata de un espacio formado por dos ejes perpendiculares, el eje X (horizontal) y el eje Y (vertical). Cada uno de estos ejes se puede tratar como una regla donde se pueden mapear variables.

Por ejemplo:

• En el eje X se puede mapear la variable edad (variable numérica discreta). La regla podría partir desde cero si se recoge información que incluye a niños o podría partir desde 18 si se recoge información de mayores de edad.

• En el eje Y se puede mapear la variable estatura (variable numérica continua).

• Si se combinan ambos ejes se forma el espacio, donde cada individuo estará mapeado, con sus datos de peso y de estatura como coordenadas de ubicación en este espacio.

• El conjunto de individuos (o puntos) formará una “nube” de puntos en este espacio. Este tipo de gráfico se llama Gráfico o Diagrama de Dispersión.

Ahora presentaremos un ejemplo más político. Esta base incluye información a nivel departamental, sociodemográfica y electoral de 2016, todas variables numéricas.

library(rio)
data = import("bases/voto2021_v2.xlsx")

Para empezar usaremos dos variables para general el gráfico de dispersión:

• En el eje X se mapeará el porcentaje de analfabetismo (variable: Analfabetismo).

• En el eje Y se mapeará el porcentaje de voto a Perú Libre en primera vuelta de 2021 (variable: VotoPL_1).

library(ggplot2)
ggplot(data, aes(x=Analfabetismo, y=VotoPL_1))+
  geom_point()+
  geom_text(data=data, aes(label=Departamento), 
            cex=2, nudge_y = 1.1, check_overlap = T)+ #Pata etiquetar los puntos, darles un tamaño, ubicación y prevenir que se sobrepongan
  labs(x="Porcentaje de analfabetismo", 
       y="Voto a Perú Libre (1era vuelta)")+ #para etiquetar los ejes
  theme_light()

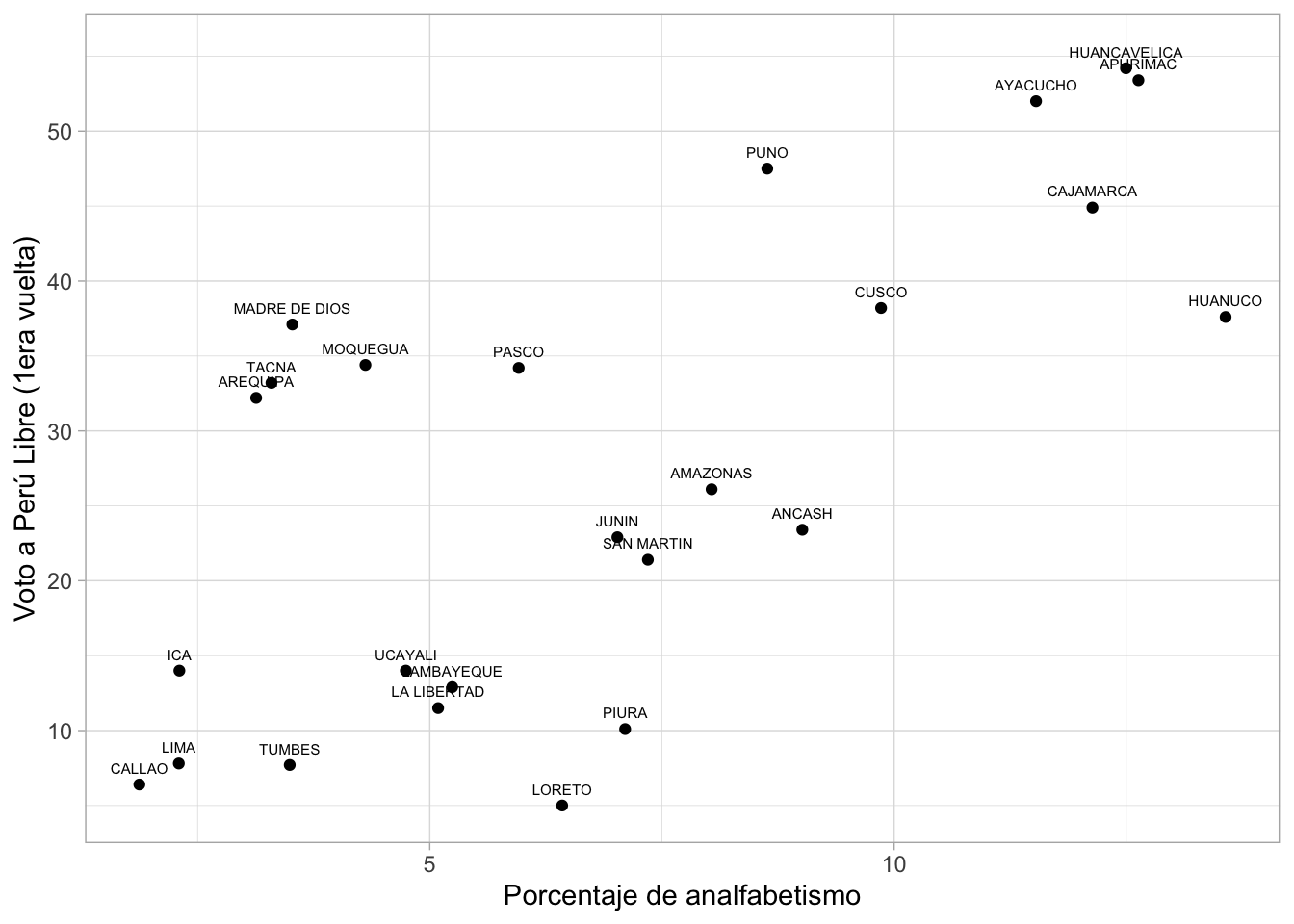
Esta “nube” de puntos nos dan una idea visual de la probable relación entre las variables. En estos casos vemos que las variables forman un patrón ascendente positivo: a medida que los departamentos reportan un mayor tasa de analfabetismo, también se observa un mayor porcentaje de voto a PL en 2021.

Por ejemplo, en el libro “El Profe” (IEP, 2021) se examina la relación entre el porcentaje de población autoidentificada como indígena y el voto a Pedro Castillo. El gráfico que se obtiene a nivel provincial es.

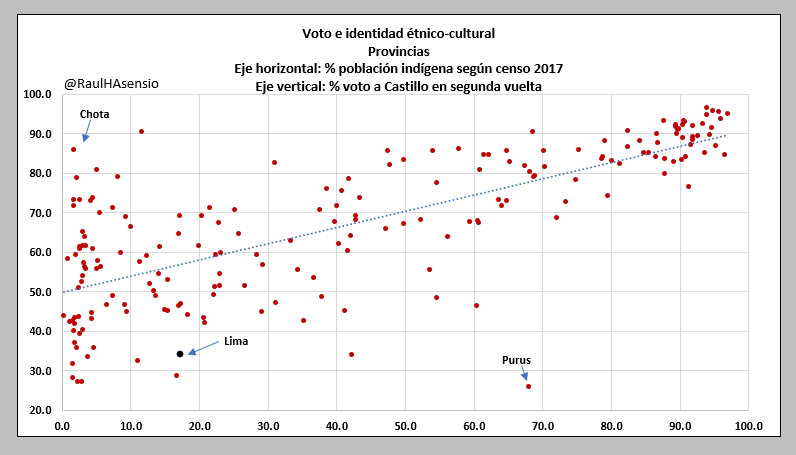
Cuando se trabaja con bases de datos con muchas más observaciones, a veces no es fácil distinguir una tendencia en la “nube” de puntos. Dado que nuestra percepción tiene esos límites, confiamos en el modelamiento mediante una relación lineal para el establecimiento de relaciones.

Relación lineal

Esta probable relación entre estas dos variables se resumen/simplifica mediante una aproximación lineal. Es decir, mediante una recta de aproximación.

Ecuación de la recta

Se tiene que recordar que una recta tiene la forma \(Y = a + bX\), donde “a” es la constante y “b” es la pendiente. Cualquier recta puede ser graficada con diferentes valores de a y b.

La relación entre las variables depende de la pendiente:

• Si b es positivo, Y aumenta cuando X aumenta. Es una relación directa / positiva.

• Si b es negativo, Y aumenta cuando X disminuye. Es una relación inversa / negativa.

• Si b es cero. Y no cambia cuando X varía. No existe relación entre las variables.

Como dijimos, la “nube” de puntos se modela mediante una recta. Esta recta de aproximación tiene la forma \(\hat{Y} = \hat{\alpha} + \hat{\beta}*X\)

Los valores que tiene el “sombrero” son datos que se calculan con los datos observados. Una vez estimados estos valores (se verá la lógica en un momento), se puede estimar un Y (por eso tiene también “sombrero”) para cualquier valor de X.

En nuestro ejemplo, se le puede pedir a ggplot que incluya la recta de aproximación en el gráfico de dispersión mediante el comando geom_smooth(method=lm, se=F), que se usa para calcular un modelo lineal (que veremos en un momento)

ggplot(data, aes(x=Analfabetismo, y=VotoPL_1))+
  geom_point()+
  geom_smooth(method=lm, se=F)+ #agregar línea de tendencia
  geom_text(data=data, aes(label=Departamento), 
            cex=2, nudge_y = 1.1, check_overlap = T)+ #Pata etiquetar los puntos, darles un tamaño, ubicación y prevenir que se sobrepongan
  labs(x="Porcentaje de analfabetismo", 
       y="Voto a Perú Libre (1era vuelta)")+ #para etiquetar los ejes
  theme_light()

## `geom_smooth()` using formula =
## 'y ~ x'

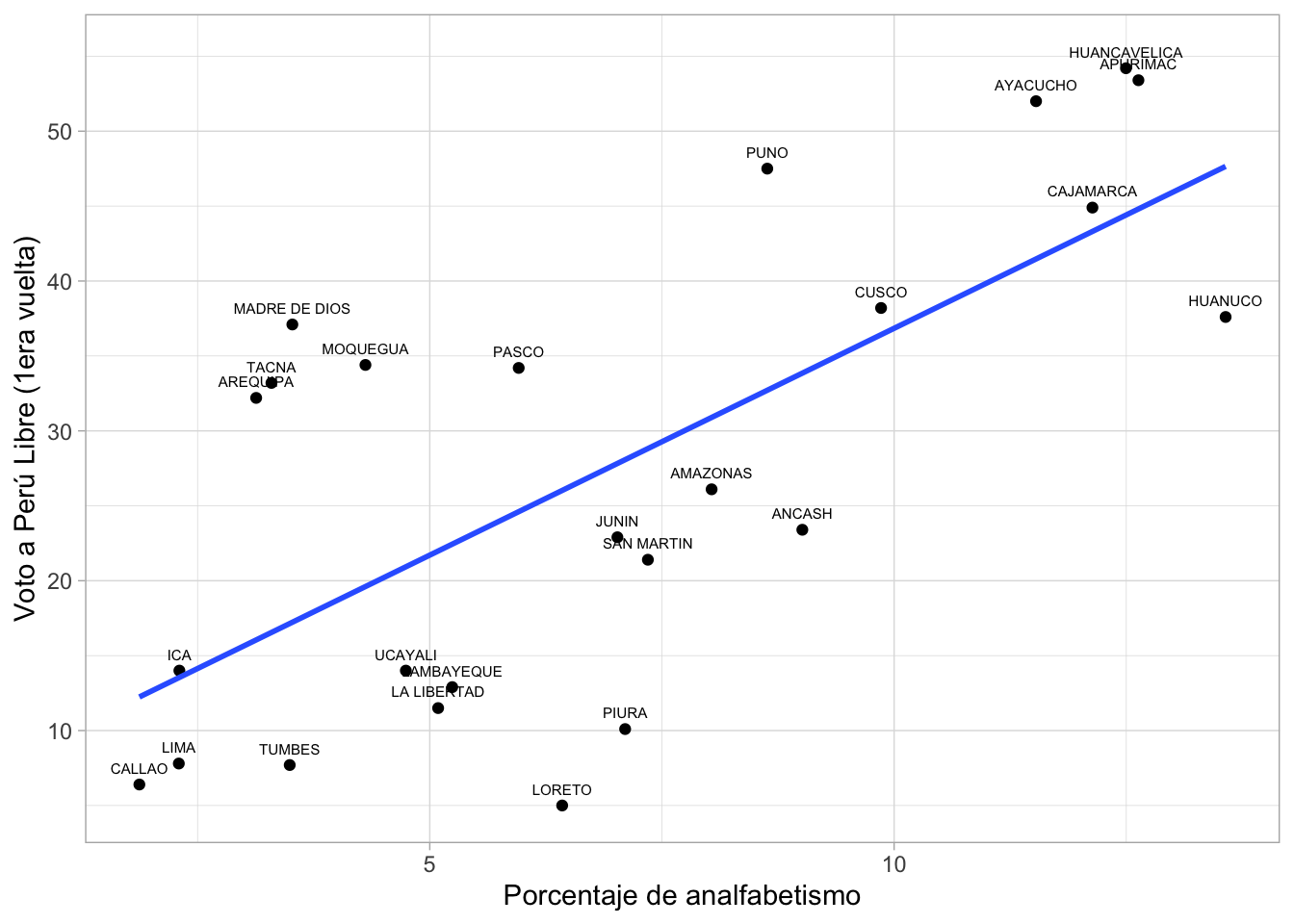
¿Cómo se calcula que ESA es la recta de aproximación, y no otra? La recta calculada se define como aquella que minimiza los residuos.

Residuos o errores

Se trata de la diferencia entre el valor observado y el valor calculado por la recta: \(Y - \hat{Y}\)

Es decir, cada observación tiene un residuo, que sería visualmente, la distancia vertical del punto a la recta de aproximación.

#Este código de abajo no se evaluará
plot(data$Analfabetismo, data$VotoPL_1,
     xlab="Porcentaje de analfabetismo por departamento",
     ylab="Voto a PL (1era vuelta)",
     pch=19, xlim=c(0,15), ylim=c(0, 55))
abline(lm(data$VotoPL_1 ~ data$Analfabetismo))
fitted = predict(lm(data$VotoPL_1 ~ data$Analfabetismo))
for (i in 1:25) {
  lines( c(data$Analfabetismo[i], data$Analfabetismo[i]), c(data$VotoPL_1[i], fitted[i]), col="blue")
}

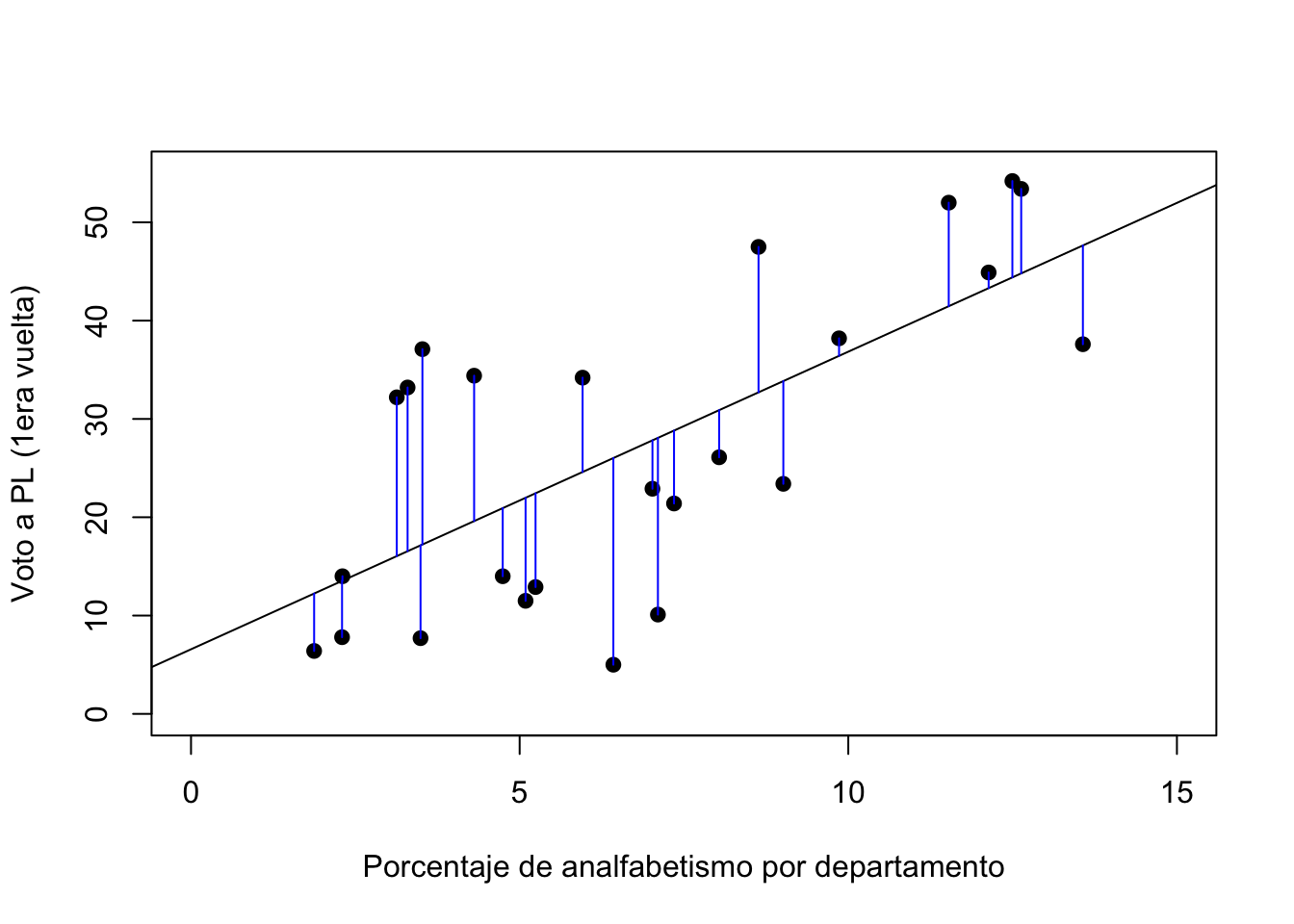
Cada punto se aproxima o se aleja más de la recta de aproximación. Estas distancias se pueden sumar para darnos una idea de qué tan bien esta recta “resume” la distribución de los datos.

Se define la recta de aproximación como la recta que minimiza esta suma de residuos. Es decir, cualquier otra recta tendría una mayor suma de esas líneas azules. Esta recta tiene una ecuación de la recta, con una constante y una pendiente específica. De manera formal la suma se hace de los residuos al cuadrado para evitar los valores negativos.

Para esto se tiene que calcular el modelo lineal con el comando lm, y esto modelo se guarda en un objeto “modelo1”.

modelo1 = lm(data$VotoPL_1 ~ data$Analfabetismo)

summary(modelo1)

## 
## Call:
## lm(formula = data$VotoPL_1 ~ data$Analfabetismo)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -21.023  -9.442  -4.795   9.798  19.872 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          6.5710     5.1709   1.271 0.216516    
## data$Analfabetismo   3.0273     0.6716   4.507 0.000159 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.85 on 23 degrees of freedom
## Multiple R-squared:  0.469,  Adjusted R-squared:  0.4459 
## F-statistic: 20.32 on 1 and 23 DF,  p-value: 0.0001589

Recta de aproximación

Los primeros datos a analizar están en la columna “Estimate”. Estos datos definen la ecuación de la recta. Según estos datos se tendría \[\hat{Y} = 6.57 + 3.03*X\]

Modelo lineal

Como indicamos, la relación entre dos variables cuantitativas se modela mediante una recta de aproximación. Para evaluar una relación entre dos variables numéricas, tenemos que responder las siguientes preguntas:

• ¿Existe asociación?

• ¿En qué dirección?

• ¿Con qué fuerza?

• Predecir para valores significativos

Predicción

Con esta ecuación se puede estimar el valor de Y (es decir, el voto a PL) para cualquier valor de X (de analfabetismo).

Por ejemplo, en Amazonas se tiene 8.03% de tasa de analfabetismo, según la base de datos. De acuerdo a la ecuación, el voto estimado a PL sería 6.57 + 3.03*8.03 = 30.9%.

El voto observado a PL en Amazonas fue 26.1%. Por lo tanto, el residuo de esta observación es 26.1-30.9 = -4.8. Este es el error de predicción.

El voto predicho a PL no solo se puede calcular para los valores observados de acceso a internet, sino también para cualquier valor de X.

¿Cuánto sería el voto predicho a PL en un departamento con cero analfabetismo? ¿cuánto sería el voto predicho a PL en un departamento con total analfabetismo?

Estas dos preguntas implican el cálculo de \(\hat{Y}\) para cuando X=0 (en la primera pregunta) y para cuando X=100 (en la segunda pregunta). En la realidad no tenemos dos departamentos con estos valores de X, pero estos se pueden predecir a partir del modelo generado.

Correlación no es causalidad

Que se pueda graficar los datos de dos variables en un espacio cartesiano y que se pueda calcular la mejor recta de aproximación NO significa que ambas variables necesariamente están relacionadas o que haya una relación de causalidad.

Para establecer una relación de causalidad hace falta:

• Que haya consistencia entre varios estudios: un estudio (casi) nunca es suficiente para definir un hallazgo. La convergencia entre diferentes estudios (en diferentes lugares y tiempos) le da mayor robustez a la relación entre dos variables.

• Que haya una (fuerza de) asociación: que existe una correlación es un primer paso para poder luego evaluar una probable causalidad. La relación es una estadística y no una relación determinista.

• Un mecanismo: una explicación basada en la teoría que defienda porqué es plausible hablar de una probable relación entre esas dos variables.

• Temporalidad: que la causa preceda al efecto. Es decir que la medición del X sea anterior a la del Y. En nuestro ejemplo, no se podría hablar de causalidad si el X hubiera sido medido antes de 2021.

Un ejemplo que cumple estas condiciones es la relación entre consumo de tabaco y desarrollo de cáncer de pulmón.

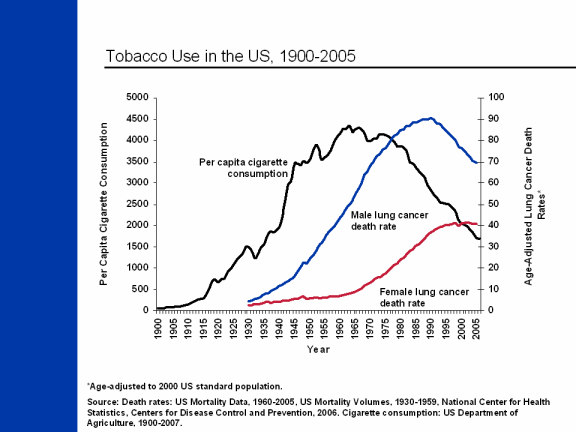
Para establecer una relación de causalidad entre ambas variables se han realizado múltiples estudios, se tiene una relación estadística robusta, se tiene un mecanismo en la nicotina y se tiene una secuencia temporal, se fuma y luego se desarrolla el cáncer de pulmón.

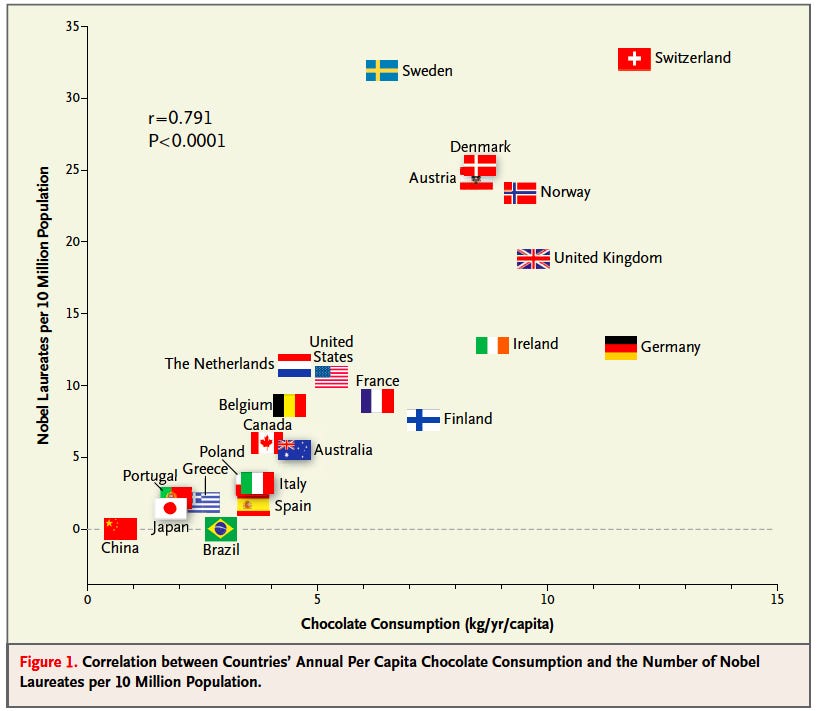
Por ejemplo, puede existir una correlación entre el consumo de chocolate en un país y el número de premios Nobel que cuente ese país.La pregunta es cuál es el mecanismo explicativo entre una variable y la otra. Pueden ver más correlaciones locas es este link.

En algunos casos, la relación entre dos variables en realidad es explicada por una tercera variable. En este tipo de casos se habla de correlaciones espúreas. Por ejemplo:

De manera más gráfica:

¿Existe una asociación o relación entre las variables?

Según estos resultados la ecuación de la recta es:
\[\hat{Y} = 6.57 + 3.03*X\]

En esta ecuación, el dato que marca la relación entre ambas variables es la pendiente. El \(\hat{\beta} = +3.03\). Este dato es una aproximación desde los datos del “verdadero” valor de \(\beta\). Como toda aproximación a partir de datos, este valor de \(\hat{\beta}\) tiene un error estándar y por lo tanto un intervalo de confianza de posibles valores del parámetro poblacional. Con el estimado y el error estándar se puede usar la distribución t para inferir a la población.

La H0: \(\beta = 0\)

La HA: \(\beta \not= 0\)

Es decir, se pone a prueba cuál es la probabilidad de observar una pendiente de 3.03 si la “verdadera” pendiente es cero. Esta probabilidad se mide, como siempre, con el p-value (o Pr(>|t|), en la tabla de resultados).

En la fila correspondiente a la variable independiente se observa que el p-value = 0.000159 (o 0.0159%). Es decir, que tenemos muy bajas probabilidades de observar una pendiente de 3.03 si la verdadera pendiente es cero. Como este valor es menor a 0.05, se puede rechazar la H0.

Con esto se concluye que se puede decir que SÍ hay una (cor)relación entre ambas variables.

Dirección

La dirección de la relación entre las variables está marcada por el signo de la pendiente. Si el signo es positivo, la recta de aproximación tiene pendiente positiva y eso indica una relación positiva entre las variables (a mayor X, mayor Y). Si el signo es negativo, la recta de aproximación tiene una pendiente negativa y eso indica una relación negativa entre las variables (a mayor X, menor Y).

En nuestro ejemplo, la pendiente (es decir, el valor de \(\hat{\beta}\)) es positiva. Eso quiere decir que departamentos que presentan mayores tasas de analfabetismo, reportan, en promedio, un mayor voto hacia Pedro Castillo.

Coeficiente de correlación de Pearson

El valor de \(\hat{\beta}\) indica la tasa de cambio, es decir, por cada unidad de cambio en X, Y cambia \(\hat{\beta}\) unidades. En nuestro ejemplo, por cada 1% de aumento en la tasa de analfabetismo, el voto a Pedro Castillo cambia 3%.

Pero la pendiente no es un buen indicador de la relación entre las variables, pues depende de las unidades de medida de las variables. Para poder evaluar la relación entre las variables, requerimos una versión estandarizada de la pendiente, que mida el cambio en unidades de desviación estándar.

Esta medida es el coeficiente de correlación de Pearson. Este coeficiente no solo mide el cambio entre las variables en unidades de desviación estándar, sino también el grado de ajuste de los puntos a la recta. Este coeficiente tiene las siguientes características:

• El coeficiente r de Pearson varía entre -1 y +1. El coeficiente r tiene el mismo signo que la pendiente.

• r=0 si la pendiente también es cero.

• r=+1 o r=-1 si todos los puntos caen en la línea de predicción. Es decir, que la predicción es “perfecta”. Esta situación es hipótetica, nunca se da con datos en ciencias sociales.

En nuestro ejemplo r=0.685. Es decir, por cada unidad de desviación estándar de cambio en X, Y cambia 0.685 desviaciones estándar.

cor.test(x=data$Analfabetismo, y=data$VotoPL_1, method="pearson")

## 
##  Pearson's product-moment correlation
## 
## data:  data$Analfabetismo and data$VotoPL_1
## t = 4.5073, df = 23, p-value = 0.0001589
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.3972054 0.8499737
## sample estimates:
##       cor 
## 0.6848503

Para tener una idea acerca de cómo interpretar este valor, la siguiente imagen muestra ejemplos de distribuciones de puntos a diferentes valores de r.

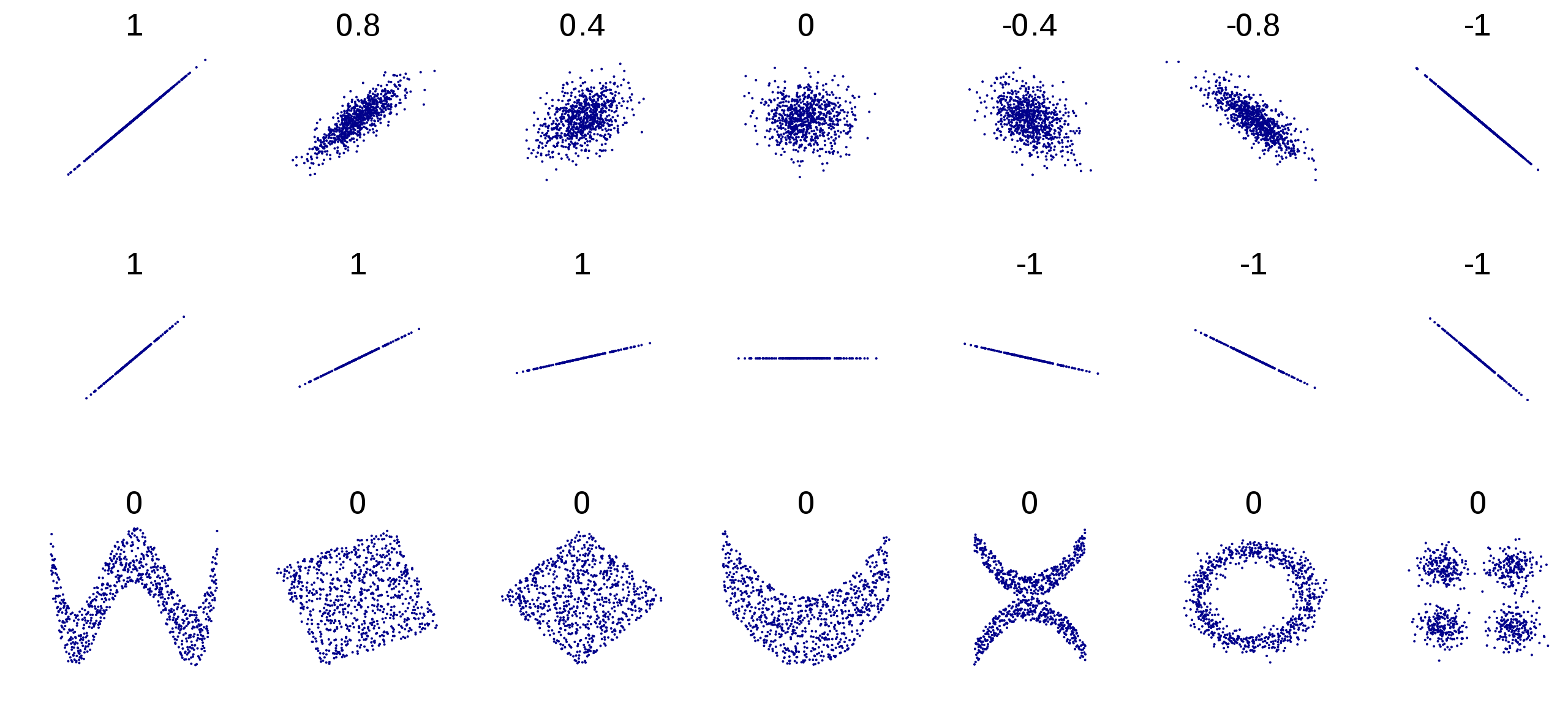
Como se observa, a medida que el valor de r se acerca a 1, los puntos se encuentran más alineados a la recta de predicción, por lo que habría menos residuos, llegando a cero, con puntos completamente ajustados a la recta.

A medida que el valor de r se acerca a cero, los puntos se vuelven más dispersos, formando una nube de puntos. Esos puntos se ajustan menos a una recta de predicción.

Para tener una idea más lúdica de la distribución de puntos a diferentes valores del coeficiente de Pearson, pueden entrar a este link de Guess the Correlation, que “gamifica” acertar con el valor de r para diferentes dispersiones de puntos.

Coeficiente de determinación \(R^2\)

En el contexto del análisis de regresión lineal, también se analiza qué tan bien X predice Y. Esta capacidad de X de predecir la variable Y se mide mediante el coeficiente de determinación \(R^2\). Este valor no es otro que el cuadrado del coeficiente de Pearson.

Pero, se interpreta como la reducción proporcional en el error al usar la recta de predicción, en lugar de sólo usar \(\bar{Y}\) (el promedio de Y) para predecir Y.

Se tiene que recordar que los errores (o residuos) son las distancias de cada punto a la recta. Cada punto tiene una distancia a la recta de \(\bar{Y}\) y también una distancia a la recta de predicción.

En la imagen de la izquierda, se muestran las distancias de los puntos a la recta de \(\bar{Y}\). Todas estas distancias al cuadrado se pueden sumar. Esta suma es E1.

En la imagen de la derecha, se muestran las distancias de los puntos a la recta de predicción \(\hat{Y}\). Todas estas distancias al cuadrado se pueden sumar. Esa suma es E2.

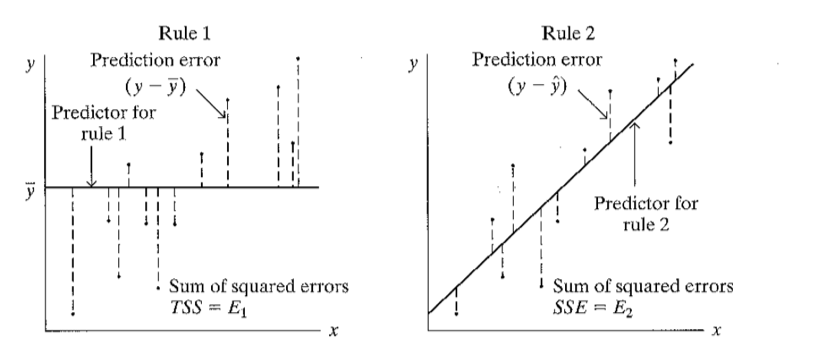
Entonces, \(R^2 = \frac{E1-E2}{E1}\). Este cálculo es igual al cuadrado del valor de la correlación. Por lo tanto:

• \(R^2\) varía entre 0 y 1.

• \(R^2=1\) implica que E2 = 0, es decir que todos los puntos caen en la recta.

• \(R^2=0\) si la pendiente es cero.

En nuestro ejemplo, \(R^2=0.47\). Este valor se encuentra en la penúltima fila del summary del modelo, con el nombre “Multiple R-squared”. Es decir, el modelo reduce un 47% el error de usar solamente el promedio para estimar Y.

Validez del modelo

La última fila del summary muestra los resultados de una prueba F, con un estadístico de la prueba y un p-value. Esta prueba es la que nos indica la validez del modelo en su conjunto.

Cuando analizamos relaciones bivariadas, este p-value es igual al p-value de la pendiente, por lo que la validez se determina con cualquiera de ellas.

Vamos a ver en la siguiente sección de análisis multivariado que el análisis de la prueba F es el primer paso, que indica la validez del modelo multivariado, y que se tiene que realizar antes de analizar los siguientes pasos, de relaciones, direcciones y fuerza.