Clase 4: Ejemplos e Intervalos de Confianza

Efectivos en las Comisarias del Perú

Pregunta: ¿los policías en el Perú están distribuidos equitativamente entre las comisarías del Perú?

¿Cómo cree que es esta distribución de datos?

Para responder a esta pregunta se usa la base de datos de comisarías del Perú de 2017. Esta base de datos está disponible en la sección Microdatos del INEI.

library(rio) 
comi17 = import("bases/comi2017.sav")

Esta base de datos incluye la pregunta sobre el número total de efectivos en cada comisaría. Esta variable se importa en R como una variable numérica, y efectivamente es el tipo de variable correcto.

class(comi17$INF110_TOT)

## [1] "numeric"

Como esta es una variable numérica, se puede describir mediante la media y la mediana.

¿Qué nos indican estos resultados?

library(tidyverse)
comi17 %>%
  summarise(Mínimo = min(INF110_TOT), 
            Mediana = median(INF110_TOT), 
            Promedio = mean(INF110_TOT),
            Máximo = max(INF110_TOT))

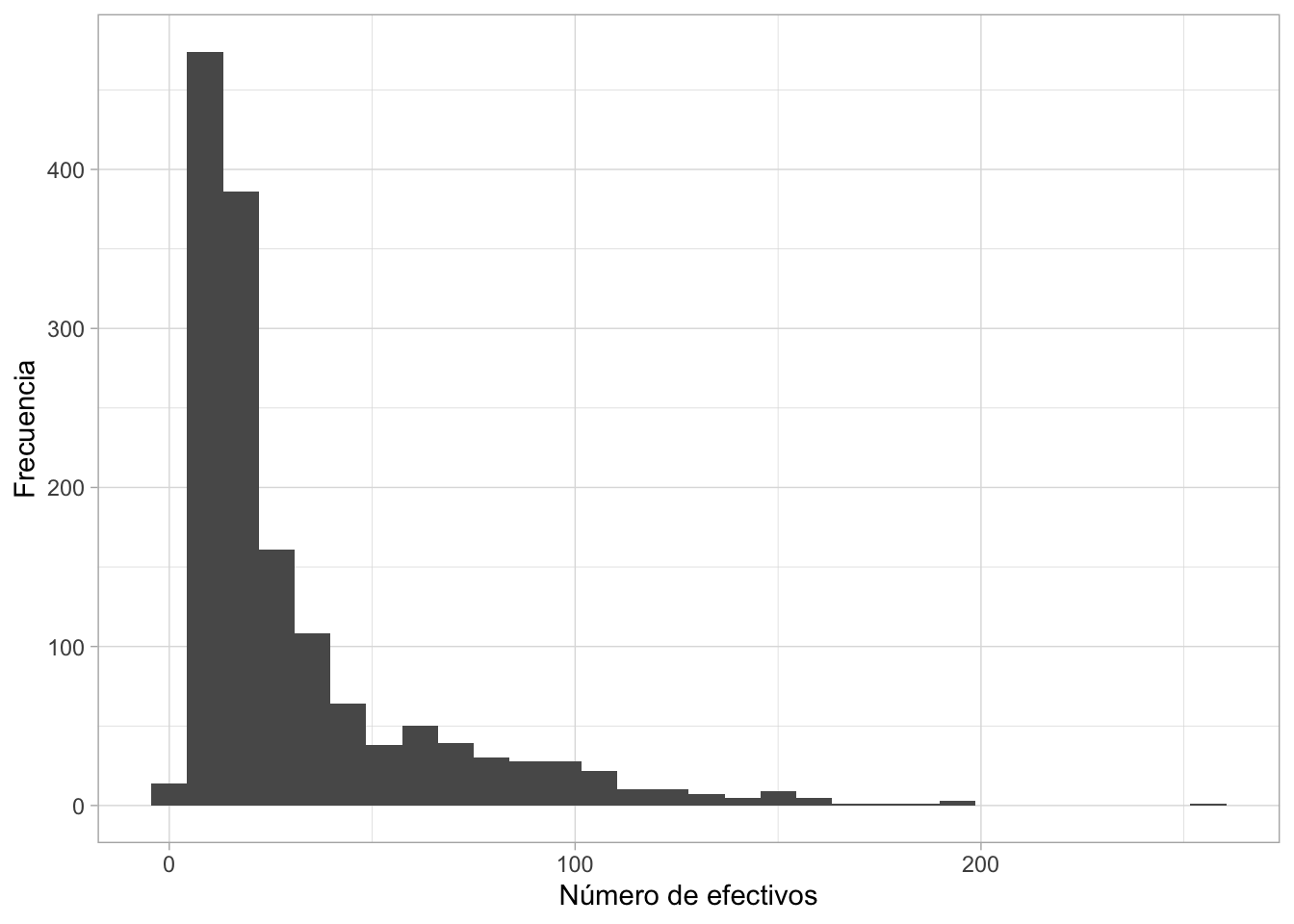
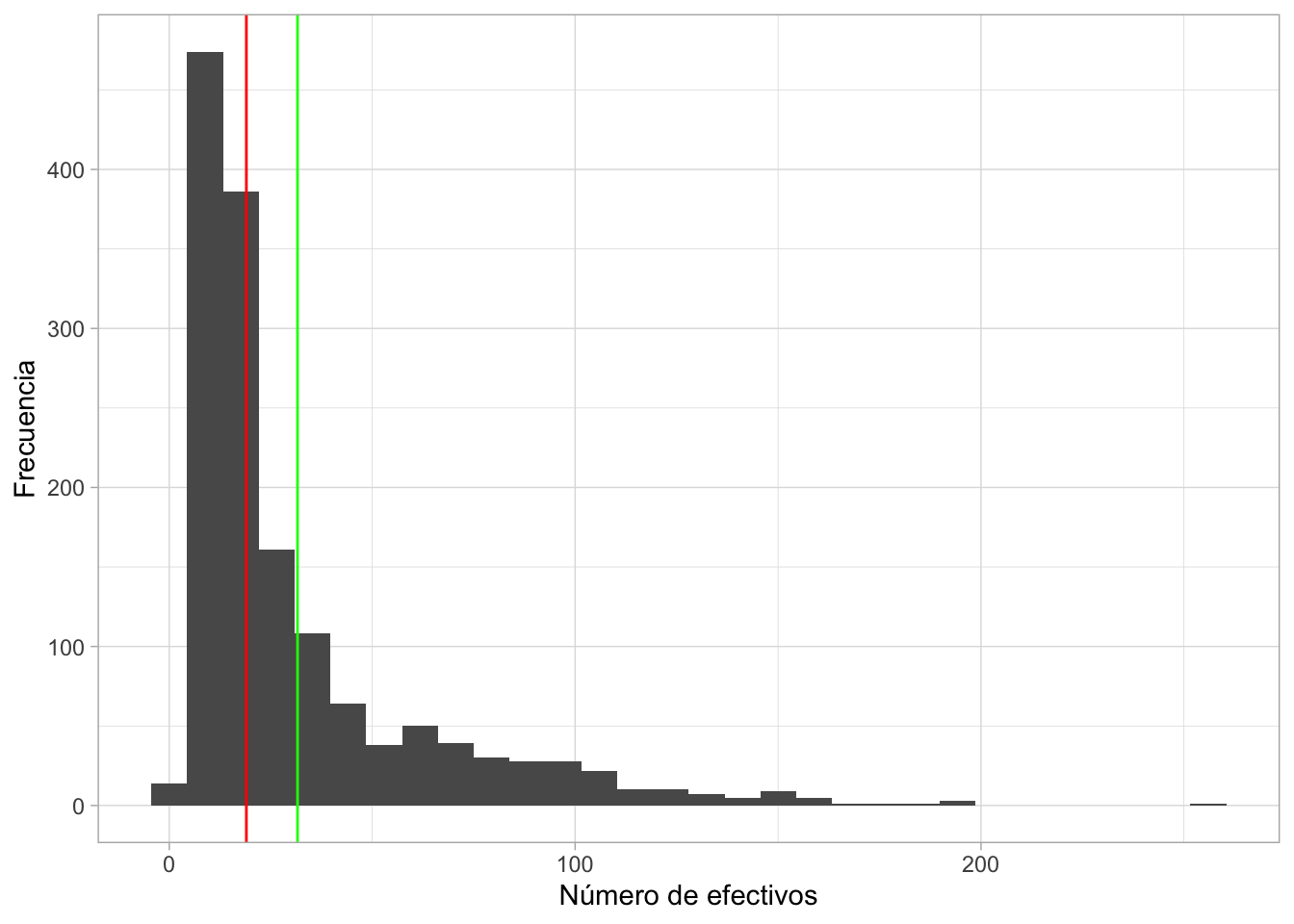
##   Mínimo Mediana Promedio Máximo
## 1      3      19 31.61538    259

Se puede graficar la distribución del número de efectivos por comisarias mediante un histograma. ¿Qué nos indica el gráfico?

library(ggplot2)
ggplot(comi17, aes(x=INF110_TOT))+
  geom_histogram()+
  xlab("Número de efectivos") +
  ylab("Frecuencia")+
  theme_light()

## `stat_bin()` using `bins = 30`.
## Pick better value with
## `binwidth`.

Se puede incluir el dato de la media y la mediana en este gráfico. ¿Cómo se interpreta la posición relativa de ambas medidas?

ggplot(comi17, aes(x=INF110_TOT))+
  geom_histogram()+
  geom_vline(xintercept = 19, color = "red")+
  geom_vline(xintercept = 31.6, color = "green")+
  xlab("Número de efectivos") +
  ylab("Frecuencia")+
  theme_light()

## `stat_bin()` using `bins = 30`.
## Pick better value with
## `binwidth`.

Ahora se quiere ver si existen diferencias en el número promedio de efectivos policiales en las comisarías del Perú entre departamentos o entre regiones. A pesar que en formulario se recoge el dato de Departamento, Provincia y Distrito, en la base de datos no se cuenta con esa información. Lo que se tiene es una variable llamada “ubigeo”. Esta variable está estandarizada de tal manera que los dos primeros dígitos corresponden al departamento, los segundos dos dígitos a las provincias y los últimos dos dígitos al distrito. Por lo tanto, para saber en qué departamento está la comisaría se requiere separar los primeros dos dígitos y guardarlos en una nueva variable.

comi17 = comi17 %>%
  mutate(dpto = str_sub(UBIGEO, 1, 2))

Copiamos el código usado para el voto 2016 y lo adaptamos a las necesidades de esta base de datos. La variable “dpto” es una variable de tipo “character” y sabemos que va desde el “01” al “25”, representando cada “número” un departamento del Perú, que hemos asociado a Costa = 1, Sierra = 2 o Selva = 3.

Entonces lo que tenemos que hallar es el código ubigeo de cada departamento y reemplazarlo por el nombre del departamento en el código original. La clasificación la guardamos en otra variable “region”.

comi17 = comi17 %>%
  mutate(region = case_when(
    dpto=="01"~3,
    dpto=="02"~2,
    dpto=="03"~2,
    dpto=="04"~2,
    dpto=="05"~2,
    dpto=="06"~2,
    dpto=="08"~2,
    dpto=="07"~1,
    dpto=="09"~2,
    dpto=="10"~3,
    dpto=="11"~1,
    dpto=="12"~2,
    dpto=="13"~1,
    dpto=="14"~1,
    dpto=="15"~1,
    dpto=="16"~3,
    dpto=="17"~3,
    dpto=="18"~1,
    dpto=="19"~2,
    dpto=="20"~1,
    dpto=="21"~2,
    dpto=="22"~3,
    dpto=="23"~1,
    dpto=="24"~1,
    dpto=="25"~3
  )) 

Esta variable “region” es de tipo numérico, pero los códigos (1, 2 y 3) no son números, sino códigos para Costa, Sierra y Selva, por lo que tenemos que crear otra variable, “region2” que sea de tipo “factor” con las etiquetas correspondientes.

library(forcats)
comi17 = comi17 %>%
  mutate(region2 = factor(region, labels=c("Costa", "Sierra", "Selva")))

Podemos usar esta variable para calcular los descriptivos del número de efectivos por región. ¿Qué conclusión saca de la tabla?

tabla1 = comi17 %>%
  group_by(region2) %>%
  summarise(Mínimo = min(INF110_TOT), 
            Mediana = median(INF110_TOT), 
            Promedio = mean(INF110_TOT),
            Desv = sd(INF110_TOT),
            Máximo = max(INF110_TOT))
tabla1

## # A tibble: 3 × 6
##   region2 Mínimo Mediana Promedio  Desv Máximo
##   <fct>    <dbl>   <dbl>    <dbl> <dbl>  <dbl>
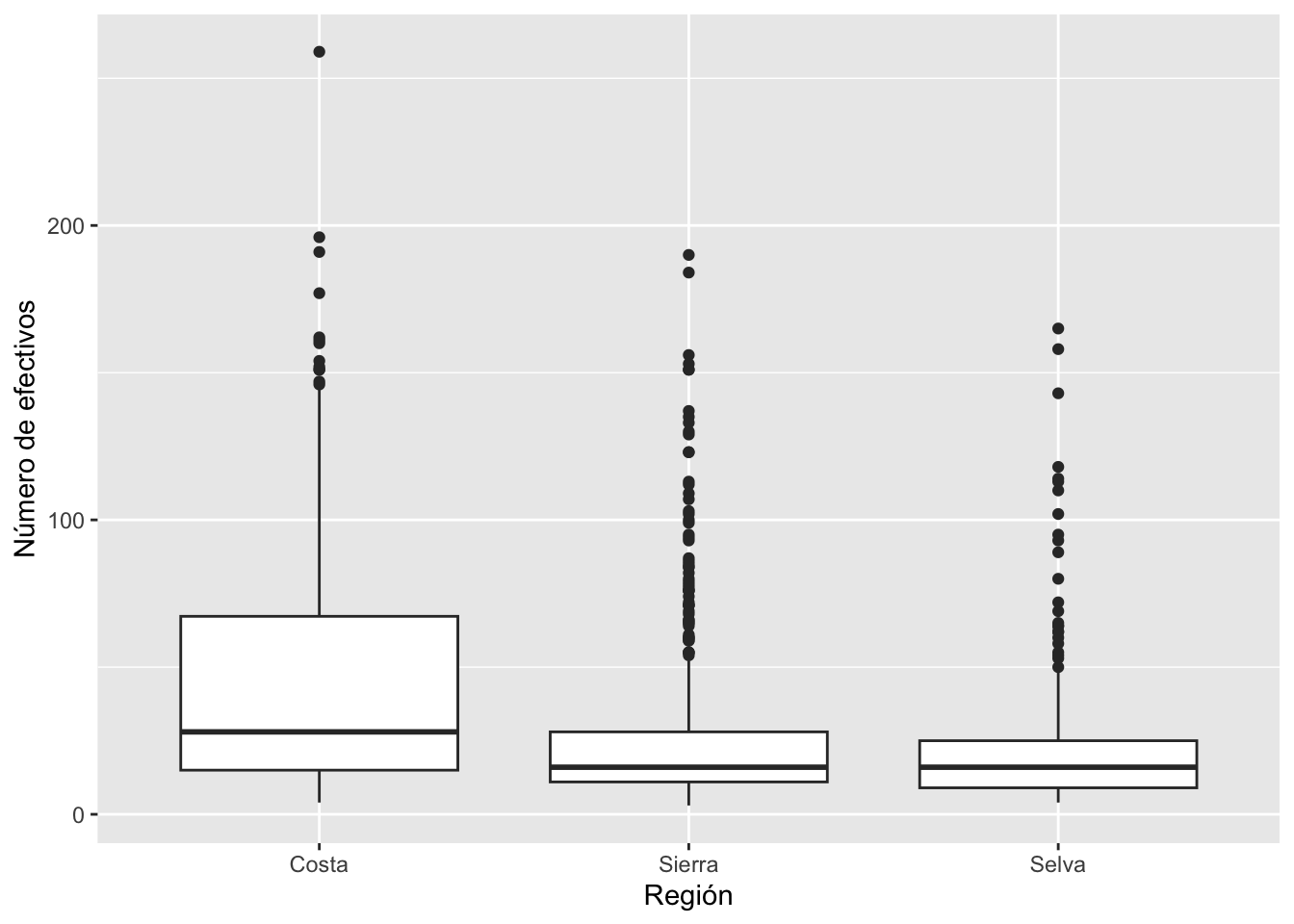
## 1 Costa        4      28     44.3  38.3    259
## 2 Sierra       3      16     24.2  24.8    190
## 3 Selva        4      16     24.0  26.5    165

Esta tabla sirve para comparar los datos descriptivos por grupos de otra variable. Algo similar se puede hacer con el gráfico de cajas, pero comparando medianas y rangos intercuartiles.

ggplot(comi17, aes(y=INF110_TOT, x=region2))+
  geom_boxplot()+
  ylab("Número de efectivos")+
  xlab("Región")+
  theme_get()

Servicios básicos en las comisarías del Perú

Pregunta: ¿Las comisarías del Perú cuentan con servicios básicos?

Para responder estas preguntas, la Encuesta Nacional de Comisarías de 2017 tiene otro módulo sobre infraestructura. Cargamos esa base de datos.

library(rio)
comi17_2 = import("bases/comi2017_2.sav")

Esta base incluye la pregunta INF216 sobre luz eléctrica, la pregunta INF225 sobre agua potable, la pregunta INF230 sobre desagüe y la pregunta INF264_E sobre el servicio de internet.

En primer lugar verificamos cómo se importan las variables. Vemos que se importan como variables numéricas. La variable sobre luz tiene opciones Si = 1 y No = 2. Esta variable es en realidad una de tipo factor.

class(comi17_2$INF216)

## [1] "numeric"

table(comi17_2$INF216)

## 
##    1    2 
## 1485    9

Se procede a crear otra variable “luz”, como la factorización de INF216 con etiquetas Sí y No.

library(tidyverse)
comi17_2 = comi17_2 %>%
  mutate(luz = factor(INF216, labels=c("Sí", "No")))

Esta variable incluye algunas comisarías donde no se tiene el dato, por lo que cuando se calcula la tabla, se filtra solo las respuestas Sí y No. Se guarda los resultados en un objeto “tabla2”.

tabla2 = comi17_2 %>%
  filter(luz == "Sí" | luz == "No") %>%
  count(Luz = luz, name="Frecuencia")
tabla2

##   Luz Frecuencia
## 1  Sí       1485
## 2  No          9

Se añade a este mismo objeto los porcentajes. ¿Qué conclusiones saca de estos resultados?

tabla2 = tabla2 %>%
  mutate(Porcentaje = (Frecuencia / sum(Frecuencia)*100 ))
tabla2

##   Luz Frecuencia Porcentaje
## 1  Sí       1485 99.3975904
## 2  No          9  0.6024096

Se hace el mismo procedimiento con la variable sobre agua potable. En este caso, la variable tiene cinco valores.

class(comi17_2$INF225)

## [1] "numeric"

table(comi17_2$INF225)

## 
##    1    3    4    5    6 
## 1424   28   30   12    1

comi17_2 = comi17_2 %>%
  mutate(agua = factor(INF225, labels=c("Red pública dentro del local", 
                                        "Camión cisterna",
                                        "Pozo",
                                        "Río, acequia o manantial",
                                        "Otro")))
table(comi17_2$agua)

## 
## Red pública dentro del local              Camión cisterna 
##                         1424                           28 
##                         Pozo     Río, acequia o manantial 
##                           30                           12 
##                         Otro 
##                            1

Se calcula la tabla de distribución de frecuencias, con el cálculo de los porcentajes en el mismo código. ¿Qué conclusiones saca de estos resultados?

tabla3 = comi17_2 %>%
  count(Agua = agua, name="Frecuencia") %>%
  mutate(Porcentaje = (Frecuencia / sum(Frecuencia)*100 ))
tabla3

##                           Agua Frecuencia  Porcentaje
## 1 Red pública dentro del local       1424 95.25083612
## 2              Camión cisterna         28  1.87290970
## 3                         Pozo         30  2.00668896
## 4     Río, acequia o manantial         12  0.80267559
## 5                         Otro          1  0.06688963

¿Qué conclusiones saca de estos resultados?

Finalmente, se hace lo mismo para la pregunta sobre internet.

class(comi17_2$INF264_E)

## [1] "numeric"

table(comi17_2$INF264_E)

## 
##   1   2   3   4 
## 127 950 132 286

comi17_2 = comi17_2 %>%
  mutate(internet = factor(INF264_E, labels=c("Sí, pago pendiente", 
                                        "Sí, pago al día",
                                        "Sí, no sabe del pago",
                                        "No cuenta con el servicio")))
table(comi17_2$internet)

## 
##        Sí, pago pendiente           Sí, pago al día      Sí, no sabe del pago 
##                       127                       950                       132 
## No cuenta con el servicio 
##                       286

¿Qué conclusiones saca sobre estos resultados?

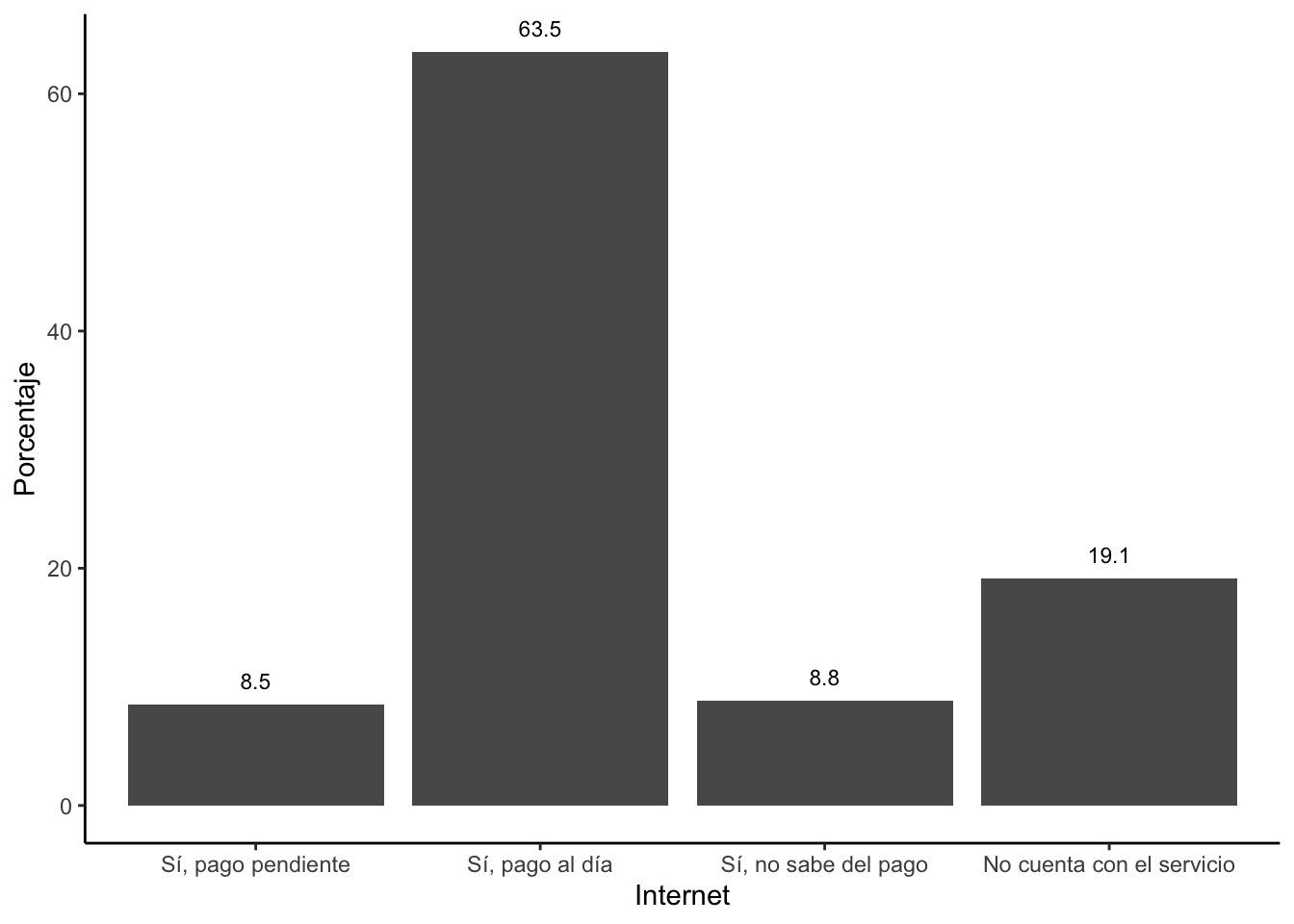
tabla5 = comi17_2 %>%
  count(Internet = internet, name="Frecuencia") %>%
  mutate(Porcentaje = (Frecuencia / sum(Frecuencia)*100 ))
tabla5

##                    Internet Frecuencia Porcentaje
## 1        Sí, pago pendiente        127   8.494983
## 2           Sí, pago al día        950  63.545151
## 3      Sí, no sabe del pago        132   8.829431
## 4 No cuenta con el servicio        286  19.130435

Este tipo de variables, de tipo factor, se puede visualizar con gráficos de barras.

graf1 = ggplot(tabla5, aes(x=Internet, y=Porcentaje))+
  geom_bar(stat="identity")+
   geom_text(aes(label=paste(round(Porcentaje, 1))), vjust=-1, size=3)+
  labs(x="Internet", y="Porcentaje")+
  theme_classic()
graf1

Tarea

Calcule las tablas de distribución de frecuencias de luz y de internet por regiones. Grafique.

Pruebas de significancia

Es una de las técnicas más usadas para el análisis en ciencias sociales. Sirve, por ejemplo, para comparar entre grupos:

• Comparar la media de ingresos de hombres y mujeres

• Comparar la proporción de personas que votarán a candidato X en Lima y en Regiones

• Comparar los ingresos de profesores en la gestión pública y en la gestión privada

La idea es comparar las estimaciones puntuales entre ambos grupos y también poder extrapolar estas diferencias a la población.

Vamos a comenzar por comparaciones entre solo 2 grupos (por el momento), que corresponde a una variable binaria o dicotómica, como sexo (hombres/mujeres), ámbito (urbano/rural), gestión educativa (pública/privada).

Para mostrar un ejemplo, vamos a usar el trabajo de (Galarza, Kogan, and Yamada 2012) que evalúa la discriminación en el mercado laborar entre hombres y mujeres. Estos autores enviaron CVs con exactas cualificaciones a ofertas reales de trabajo, variando solo el nombre del aplicante, con nombres de hombres y mujeres. La variable de respuesta es la tasa de respuesta a estos CVs, es decir, de cuántos CVs enviados se recibió una llamada para una entrevista.

En cualquier prueba de significancia se tiene que presentar una hipótesis nula, que generalmente es la hipótesis de no diferencias o de no efectos. Este trabajo parte de una idea que existe una discriminación de género en el mercado laboral, por lo que la hipótesis nula indicaría lo contrario. En el caso de este trabajo se tendría:

H0: Tasa de respuesta a CVs de hombres = Tasa de respuesta a CVs de mujeres

o lo que es lo mismo

H0: Tasa de respuesta a CVs de hombres - Tasa de respuesta a CVs de mujeres = 0

En ese trabajo se presenta el siguiente cuadro de resultados:

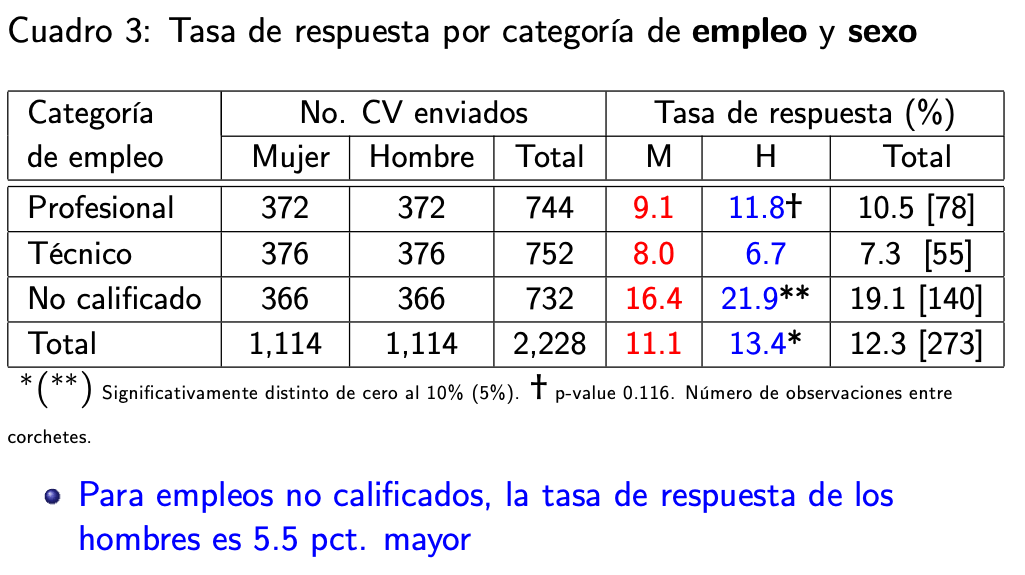
En la muestra total de 2,228 CVs enviados, mitad de CVs con nombres de hombres y la otra mitad con nombres de mujeres, todos con las mismas cualificaciones, se tiene que la tasa de respuesta para los CVs de hombres es 13.4% y para los CVs de mujeres es 11.1%.

De acuerdo a las estimaciones puntuales, efectivamente, los hombres tienen una mayor tasa de respuesta a sus CVs que las mujeres, a iguales cualificaciones. Esta conclusión, sin embargo, es solo para las 2,228 observaciones de la muestra. ¿Cómo extrapolar esta conclusión a la población? ¿Toda diferencia puntual se validaría en la población?

Comparación de intervalos de confianza por grupos

Una primera forma “informal” para extrapolar las diferencias en las estimaciones puntuales de la muestra a la población es construyendo los intervalos de confianza para la media o para la proporción por cada uno de los subgrupos.

En este caso, por ejemplo, significaría construir el IC de la tasa de respuesta para hombre y mujeres.

Pregunta: ¿Se pueden construir los IC de cada grupo con los datos de la tabla?

Cada IC sería una extrapolación del parámetro, es decir, el rango de valores de la tasa de respuesta a los CVs de hombres para todo el mercado laboral al 95% de confianza. Lo mismo para la tasa de respuesta de las mujeres.

Una vez construidos los IC, se analiza si estos intervalos se cruzan o no se cruzan. La regla de decisión “informal” es:

• Si los IC de ambos grupos se cruzan, entonces no se puede afirmar que el parámetro de un grupo sea mayor o menos que el parámetro del otro grupo.

• Si los IC de ambos grupos NO se cruzan, entonces se puede afirmar, al 95% de confianza, que el parámetro de un grupo es mayor/menor al parámetro del otro grupo.

Ejemplo 1 para una variable numérica: ENL

Pregunta: ¿existen diferencia en la cantidad de libros que leen hombres y mujeres? ¿y entre diferentes niveles socioeconómicos?

La hipótesis cero sería:

Ho: Promedio de libros que lee un hombre = Promedio de libros que lee una mujer.

library(rio)
enl = import("/Users/Arturo/Library/CloudStorage/GoogleDrive-arturo.maldonado@pucp.pe/My Drive/A Cursos/Estadistica_1/Data/ENL2022/ENL2022.sav")

library(tidyverse)
enl = enl %>%
  mutate(sexo = factor(P209, labels=c("Hombre", "Mujer")))

enl = enl %>%
  mutate(nse1 = factor(nse, labels=c("Rural", "Bajo", "Medio", "Alto")))

library(tidyverse)
enl = enl %>%
  mutate(libros = P412_1 + P412_2)

enl %>%
  summarize(mean(P412_1, na.rm=T), 
            mean(P412_2, na.rm=T), 
            mean(libros, na.rm=T))

##   mean(P412_1, na.rm = T) mean(P412_2, na.rm = T) mean(libros, na.rm = T)
## 1                2.468012                1.376829                3.844841

tabla1 = enl %>%
  group_by(sexo) %>%
  summarize(media = mean(libros, na.rm=T), 
            mediana = median(libros, na.rm=T),
            desviacion = sd(libros, na.rm=T))
tabla1

## # A tibble: 2 × 4
##   sexo   media mediana desviacion
##   <fct>  <dbl>   <dbl>      <dbl>
## 1 Hombre  3.93       3       5.65
## 2 Mujer   3.78       3       4.86

ggplot(enl, aes(y= libros, x= sexo))+
  geom_boxplot()+
  scale_y_continuous(limits = c(0, 20))+
  ylab("Total libros leídos")+
  xlab("Sexo")+
  theme_get()

## Warning: Removed 25176 rows containing
## non-finite outside the scale
## range (`stat_boxplot()`).

El cálculo del intervalo de confianza de una media es:

\[ IC = \bar{X} \pm 1.96 * \frac{s} {\sqrt{n}} \]

Para una comparación usando los intervalos de confianza, se puede usar el comando ciMean de la librería lsr. Este comando regresa el límite inferior y el límite superior del intervalo de confianza. Por lo tanto, para guardar solo el mínimo se tiene que especificar lsr::ciMean(P1_6, na.rm=T)[1] y para el máximo cambiaría a [2].

library(lsr)
tabla2 = enl %>%
  summarise(media = mean(libros, na.rm=T),
            desv = sd(libros, na.rm = T),
            liminf = ciMean(libros, na.rm=T)[1],
            limsup = ciMean(libros, na.rm=T)[2]
            )
tabla2

##      media    desv   liminf   limsup
## 1 3.844841 5.22275 3.770435 3.919248

tabla2xsexo = enl %>%
  group_by(sexo) %>%
  summarise(media = mean(libros, na.rm=T),
            desv = sd(libros, na.rm = T),
            liminf = ciMean(libros, na.rm=T)[1],
            limsup = ciMean(libros, na.rm=T)[2]
            )
tabla2xsexo

## # A tibble: 2 × 5
##   sexo   media  desv liminf limsup
##   <fct>  <dbl> <dbl>  <dbl>  <dbl>
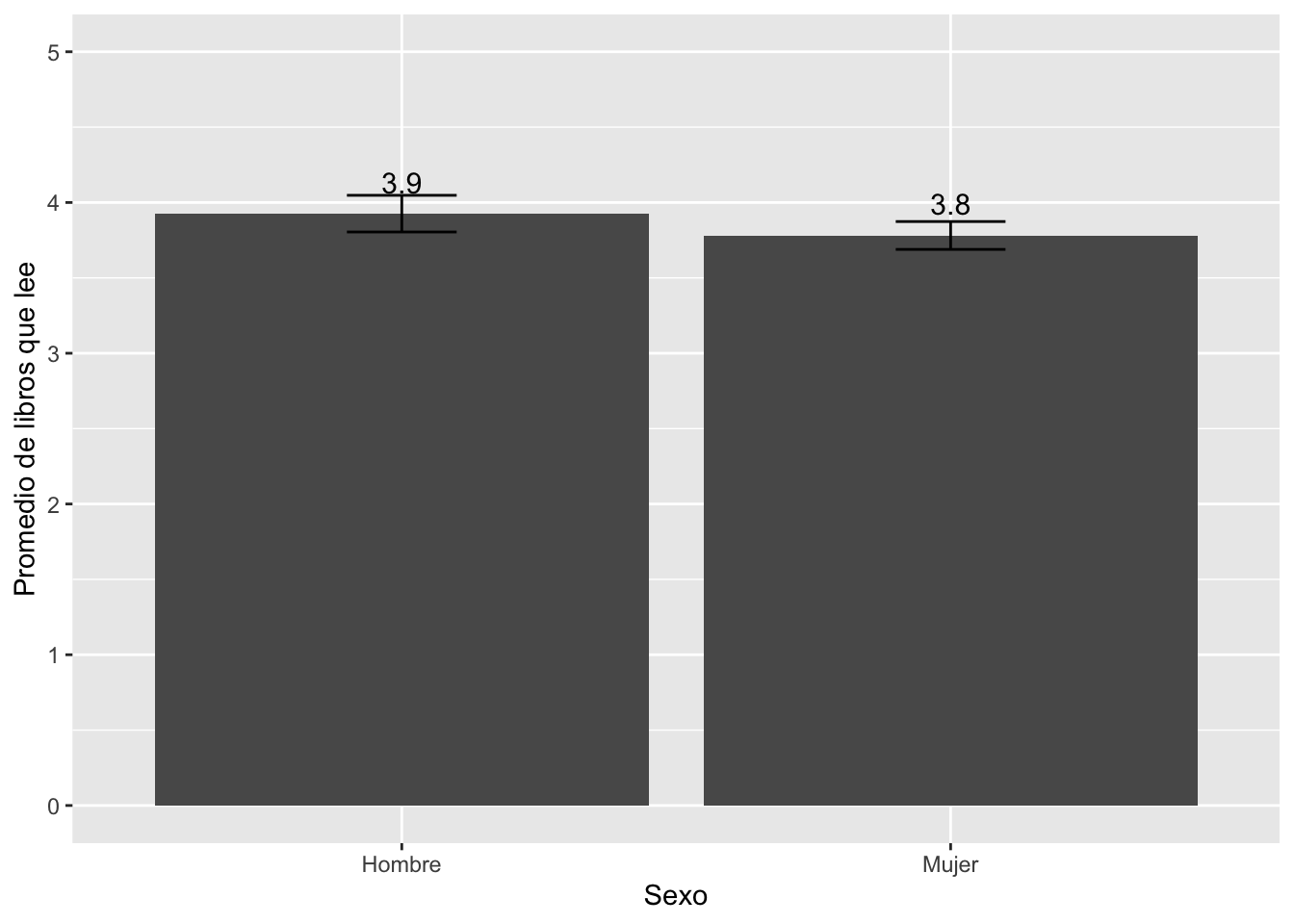
## 1 Hombre  3.93  5.65   3.80   4.05
## 2 Mujer   3.78  4.86   3.69   3.87

• El IC al 95% de confianza, el promedio de libros que lee un hombre está en el siguiente intervalo \[3.80 - 4.05\]

• El IC al 95% de confianza el libros que lee una mujer está en el siguiente intervalo \[3.69 - 3.87\]

Como ambos intervalos SÍ se traslapan, entonces NO se puede afirmar que esas diferencias se pueden extrapolar la población. NO se puede afirmar que existan diferencias entre hombres y mujeres en el número de libros que leen (sería un “empate técnico”).

Gráfico de IC para comparar medias

library(ggplot2)
graf = ggplot(tabla2xsexo, aes(x=sexo, y=media))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=round(media, 1)), vjust=-1, size=4)+
  xlab("Sexo") + ylab("Promedio de libros que lee")+
  ylim(0, 5)
graf

Ejemplo 2 para una variable numérica: ENDO

Pregunta: ¿a cuántos alumnos en promedio atiende un profesor peruano? ¿Existen diferencias de género?

Usando el ejemplo de la ENDO 2020, la hipótesis que se puede evaluar es si los profesores atienden a diferente número de alumnos de acuerdo a su sexo. Como vimos antes, las comparaciones puntuales sugieren diferencias, donde los docentes hombres atienden a más alumnos que las docentes mujeres.

La hipótesis cero sería:

Ho: Promedio de alumnos que acompaña un docente hombre = Promedio de alumnos que acompaña una docente mujer.

library(rio)
endo2020 = import("bases/ENDO_REMOTO_2020.dta")

La variable P1_1 (sexo del docente) está definida originalmente como una variable numérica (esto se puede comprobar con el código str(endo2020$P1_1). Esta variable, sin embargo es de tipo factor.

Se puede crear una nueva variable “sexo” con la variable transformada y etiquetada.

library(dplyr)
library(tidyverse)
endo2020 = endo2020 %>%
  mutate(sexo = factor(P1_1, labels=c("Hombre", "Mujer")))

endo2020 %>%
  summarize(Media = mean(P1_6, na.rm = T), 
            Desv.Std = sd(P1_6, na.rm = T))

##      Media Desv.Std
## 1 39.98644 50.76707

alumxsexo = endo2020 %>%
  group_by(sexo) %>%
  summarize(Media = mean(P1_6, na.rm = T), 
            Desv.Std = sd(P1_6, na.rm = T))
alumxsexo

## # A tibble: 3 × 3
##   sexo   Media Desv.Std
##   <fct>  <dbl>    <dbl>
## 1 Hombre  52.2     60.4
## 2 Mujer   34.1     44.2
## 3 <NA>   NaN       NA

Se encuentra que los docentes hombres acompañan a 52 alumnos en promedio, en comparación con las docentes mujeres que acompañan a 34 alumnos en promedio, es decir 18 alumnos menos en promedio.

Recordemos que el cálculo del intervalo de confianza de una media es:

\[ IC = \bar{X} \pm 1.96 * \frac{s} {\sqrt{n}} \]

Para una comparación usando los intervalos de confianza, se puede usar el comando ciMean de la librería lsr. Este comando regresa el límite inferior y el límite superior del intervalo de confianza. Por lo tanto, para guardar solo el mínimo se tiene que especificar lsr::ciMean(P1_6, na.rm=T)[1] y para el máximo cambiaría a [2].

library(lsr)
endo2020 %>%
  summarise(media = mean(P1_6, na.rm=T),
            desv = sd(P1_6, na.rm = T),
            liminf = ciMean(P1_6, na.rm=T)[1],
            limsup = ciMean(P1_6, na.rm=T)[2]
            )

##      media     desv   liminf  limsup
## 1 39.98644 50.76707 39.26358 40.7093

alumxsexo = endo2020 %>%
  group_by(sexo) %>%
  summarise(media = mean(P1_6, na.rm=T),
            desv = sd(P1_6, na.rm = T),
            liminf = ciMean(P1_6, na.rm=T)[1],
            limsup = ciMean(P1_6, na.rm=T)[2]
            )
alumxsexo

## # A tibble: 3 × 5
##   sexo   media  desv liminf limsup
##   <fct>  <dbl> <dbl>  <dbl>  <dbl>
## 1 Hombre  52.2  60.4   50.7   53.8
## 2 Mujer   34.1  44.2   33.3   34.8
## 3 <NA>   NaN    NA     NA     NA

• El IC al 95% de confianza, el promedio de alumnos que acompañan los docentes hombre está en el siguiente intervalo \[50.7 - 53.8\]

• El IC al 95% de confianza el promedio de alumnos que acompañan las docentes mujeres está en el siguiente intervalo \[33.3 - 34.8\]

Como ambos intervalos NO se traslapan (el mayor valor del segundo IC, 34.8 , es menor al mejor valor del primer IC, 50.7), entonces se puede afirmar que esas diferencias se pueden extrapolar la población.

Si los IC se traslapan, entonces, no se puede afirmar que existan diferencias en el número de alumnos que acompañan docentes hombres o mujeres (sería un “empate técnico”).

Gráfico de IC para comparar medias

Se puede graficar ambos intervalos de confianza. Para hacer esto, usaremos la tabla que guarda los datos de los intervalos de confianza.

Esta tabla, sin embargo, tiene una fila de resultados para los valores perdidos. Esta fila no tiene datos por graficar, por lo que tenemos que eliminarla.

Los dataframes se organizan en filas y columnas. La table “ci_alumxsexo” tiene 3 filas y 3 columnas. La tercera fila es la que no tiene datos que graficar. Para eliminar se tiene que especificar la tabla y con los brackets [filas, columnas] definir los datos a eliminar [-3, ]. Se elimina con el signo “-” y como no hay datos luego de la “,”, se indica que no se cambia ninguna columna.

alumxsexo = alumxsexo[-3,]
alumxsexo

## # A tibble: 2 × 5
##   sexo   media  desv liminf limsup
##   <fct>  <dbl> <dbl>  <dbl>  <dbl>
## 1 Hombre  52.2  60.4   50.7   53.8
## 2 Mujer   34.1  44.2   33.3   34.8

Esta tabla se puede usar para crear un gráfico que compare ambos IC con la librería ggplot2 y con la geometría geom_errorbar. Se agrega geom_text para incluir el “texto” con los valores promedio de ambos grupos.

library(ggplot2)
graf1 = ggplot(alumxsexo, aes(x=sexo, y=media))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=round(media, 1)), vjust=-1, size=4)+
  xlab("Sexo del docente") + ylab("Promedio de alumnos")+
  ylim(0, 60)
graf1

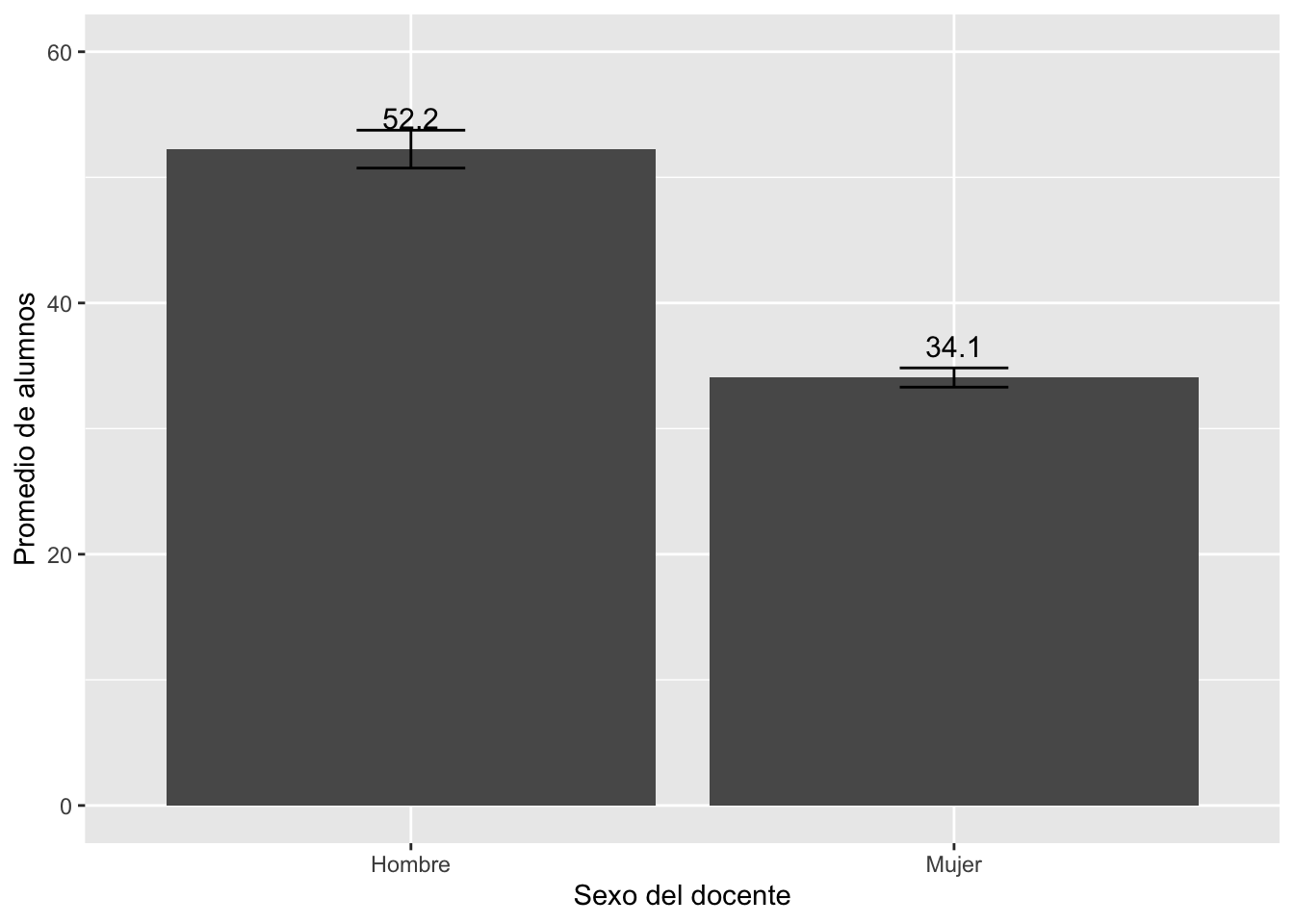
En este gráfico queda más claro que ambos IC no se traslapan por lo que se puede decir que sí existen diferencias entre docentes hombre y mujeres en el número de alumnos que acompañan en el Perú.

Este tipo de gráfico es bastante usual en los reportes estadísticos. Por ejemplo, se pueden ver este tipo de gráficos en los reportes de El Pulso de la Democracia del proyecto LAPOP. En el último reporte para Perú se presenta el siguiente gráfico que muestra los niveles de satisfacción con la democracia entre grupos de satisfacción con los servicios públicos. Estos gráficos son construidos de la misma manera que se ha construido el gráfico de arriba.

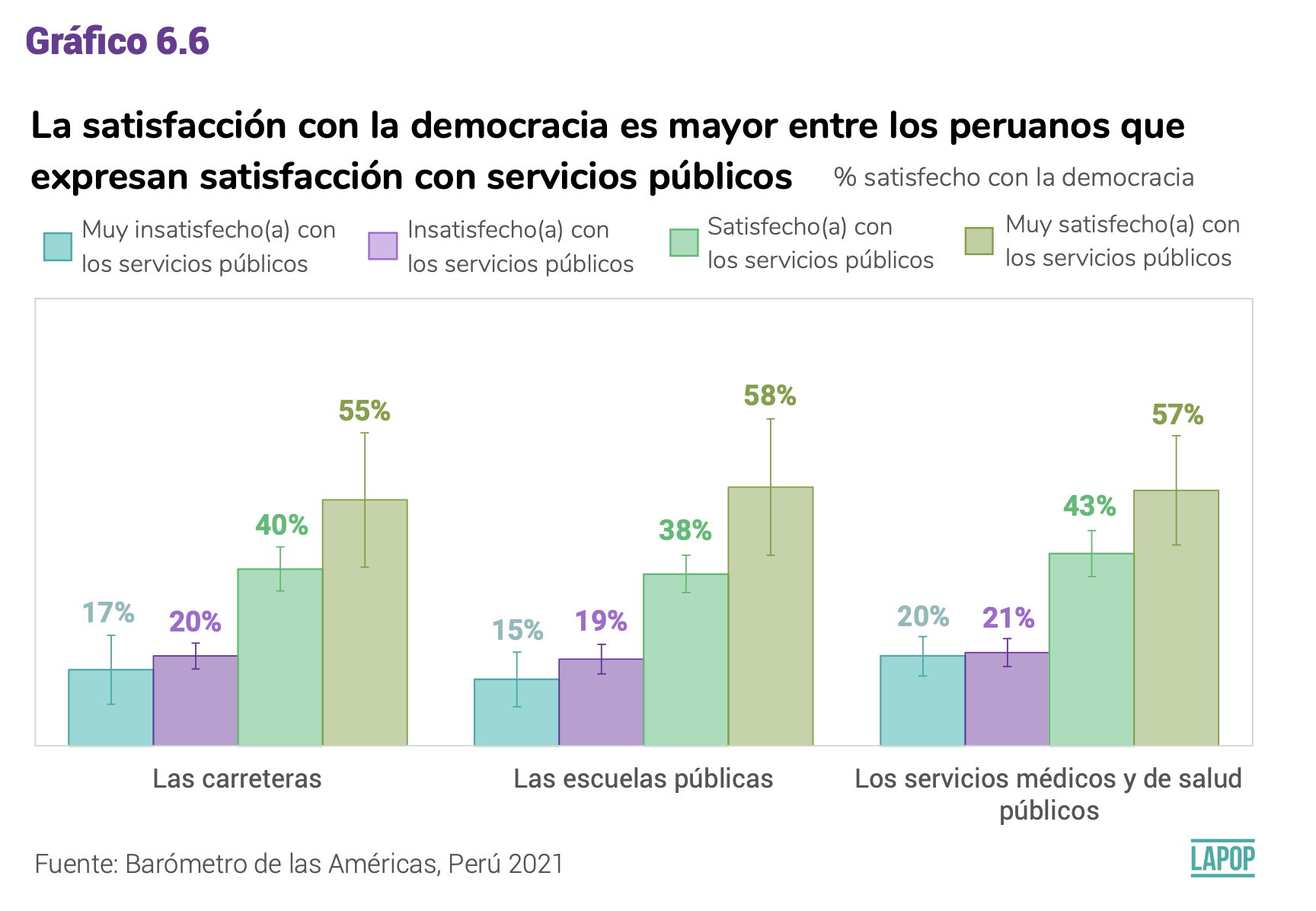
¿Por qué?. .. Aquí viene la interpretación del politólogo .

OJO: no se debe confundir este gráfico con un gráfico de cajas.

TAREA: Analizar si existen diferencias en el número de alumnos entre docentes con diferentes condiciones laborales (P1_7).

Ejemplo 3 para una variable numérica: LAPOP

library(rio)
lapop = import("bases/PER_2023_LAPOP_AmericasBarometer_v1.0_w.sav")

Ejemplo para variable numérica con índice aditivo

El cuestionario de LAPOP incluye dos preguntas sobre las fuerzas del orden. B12. ¿Hasta qué punto tiene usted confianza en las Fuerzas Armadas? y B18. ¿Hasta qué punto tiene usted confianza en la policía nacional?

Ambas preguntas están medidas en una escala de 1 a 7, donde 1 significa “Nada” y 7 significa “Mucho”. Una persona que tenga desconfianza de las fuerzas del orden en general, seguramente reportará puntajes bajos en ambas preguntas. Por el contrario, una persona que tenga alta confianza en las fuerzas del orden en general, puede reportar puntajes altos en ambas preguntas.

Se pueden combinar ambas preguntas para generar un índice aditivo de confianza general en las fuerzas del orden, como la suma de ambas. Como cada pregunta puede ser respondida entre 1 y 7, la suma puede variar entre 2 y 14. Un puntaje de 2 expresará la más baja confianza en las fuerzas del orden. Un puntaje de 14, la más alta confianza en las fuerzas del orden. Cualquier puntaje intermedio, expresará una confianza intermedia.

Como NO es intuitivo tener un índice que varíe entre 2 y 14, se puede restar dos a la suma para que el índice varíe entre 0 y 12. Como esta variación tampoco es intuitiva, se puede dividir todo entre 12 para que el índice varíe entre 0 y 1.

	Confianza en FFAA	Confianza en policía	Confianza general	Confianza general - 2	(Confianza general - 2) / 12	(Confianza general - 2) / 12*100
Persona con mucha desconfianza en las fuerzas del orden	1	1	2	0	0	0
Persona con mucha confianza en las fuerzas del orden	7	7	14	12	1	100
Persona con confianza media en las fuerzas del orden	4	5	9	7	0.58	58
Persona con confianza media en las fuerzas del orden	6	4	10	8	0.66	66

De esta manera cada persona tiene un puntaje que puede variar entre 0 y 1, dependiendo de las respuestas que dio a cada una de las preguntas individuales.

Esto se puede calcular en R.

library(tidyverse)
lapop = lapop %>%
  mutate(indice = (b12+b18-2)/12*100)

Podemos asumir que este índice es una variable cuantitativa, por lo que podemos calcular la media y el intervalo de confianza de la media.

library(lsr)
lapop %>%
  summarise(media = mean(indice, na.rm=T),
            liminf = ciMean(indice, na.rm=T)[1],
            limsup = ciMean(indice, na.rm=T)[2]
            )

##      media   liminf  limsup
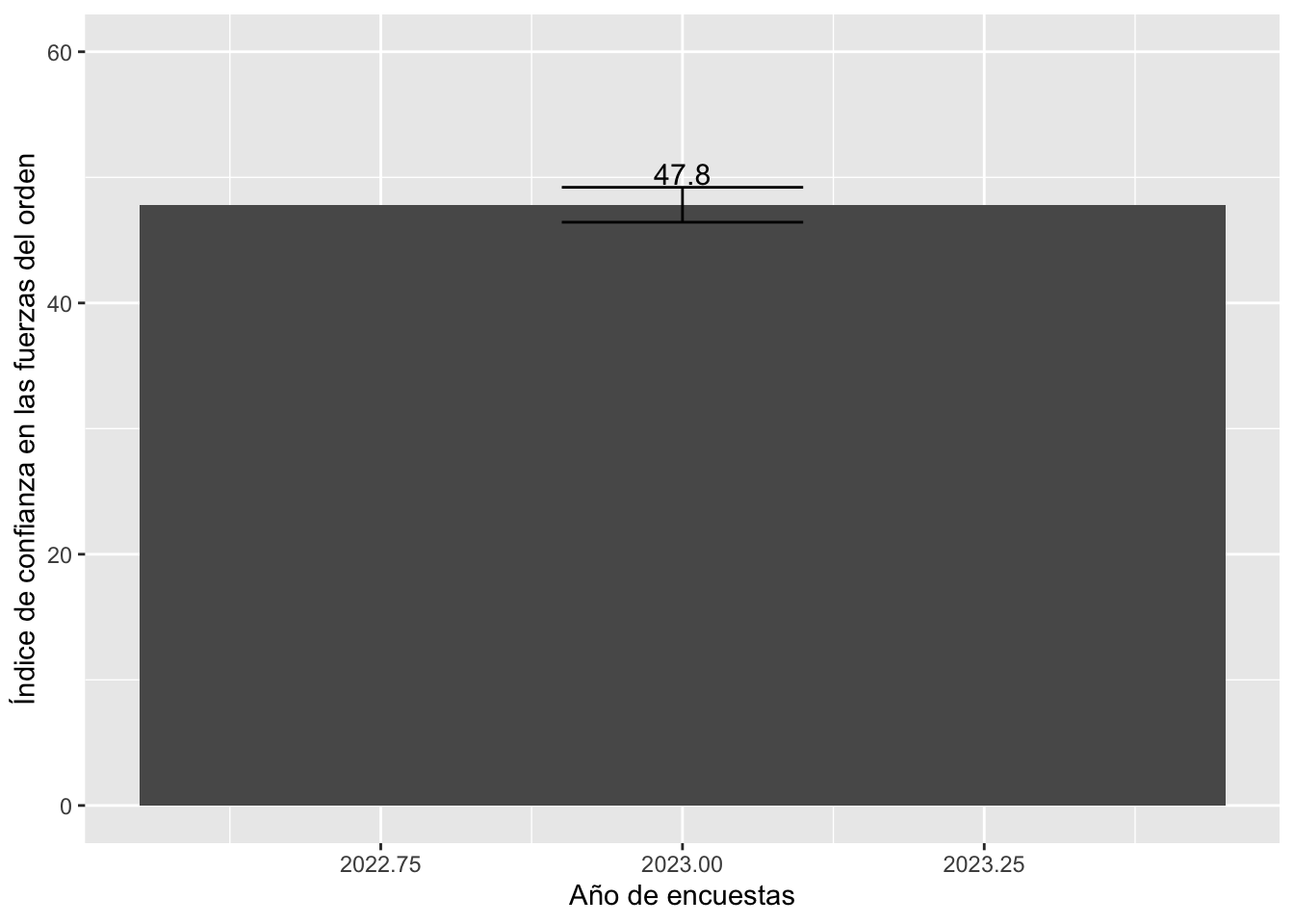
## 1 47.81916 46.42952 49.2088

Mejor aún, podemos calcular el índice de confianza en las fuerzas del orden por año de la encuesta.

indicexwave = lapop %>%
  group_by(wave) %>%
  summarise(media = mean(indice, na.rm=T),
            liminf = ciMean(indice, na.rm=T)[1],
            limsup = ciMean(indice, na.rm=T)[2]
            )
indicexwave

## # A tibble: 1 × 4
##    wave media liminf limsup
##   <dbl> <dbl>  <dbl>  <dbl>
## 1  2023  47.8   46.4   49.2

Con lo que podemos comparar el índice de apoyo a las fuerzas del orden por año para sacar conclusiones acerca de diferencias.

library(ggplot2)
graf3 = ggplot(indicexwave, aes(x=wave, y=media))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=paste(round(media, 1))), vjust=-1, size=4)+
  xlab("Año de encuestas") + ylab("Índice de confianza en las fuerzas del orden")+
  ylim(0, 60)
graf3

Ejemplo 1 para una variable categórica: ENDO

Siguiendo con el ejemplo de la ENDO 2020, la hipótesis que se puede evaluar es si existen diferencias en si los docentes han recibido apoyo psicológico o emocional por sexo (P1_13).

La hipótesis cero sería: La proporción de docentes que han recibido apoyo psicológico entre docentes hombres = Proporción de docentes que han recibido apoyo psicológico entre docentes mujeres.

Lo primero es transformar la variable P1_13 que es importada como numérica, como una variable de factor y con sus etiquetas.

endo2020 = endo2020 %>%
  mutate(apoyo = factor(P1_13, labels=c("Sí", "No")))

Ahora tenemos que producir la tabla de distribución de frecuencias. Si calculamos las frecuencias con count directamente, esta tabla incluiría una fila de los NAs y luego calculará los porcentajes incluyendo a este grupo. Es por esto que antes de calcular las frecuencias, tenemos que filtrar para que solo cuente los “Sí” y “No”. Luego de las frecuencias, incluimos el porcentaje con mutate.

tabla = endo2020 %>%
  filter(apoyo =="Sí" | apoyo == "No") %>%
  count(Apoyo = apoyo, name="N") %>%
  mutate(total = sum(N), 
         Porcentaje = N / total * 100)
tabla

##   Apoyo    N total Porcentaje
## 1    Sí 9476 18930   50.05811
## 2    No 9454 18930   49.94189

Por ejemplo, para hallar el IC de la proporción de aquellos docentes que reportaron haber recibido apoyo psicológico, podemos usar el comando prop.test. Este comando requiere el n de la opción “Sí” de la tabla y el total de casos. Por defecto nos calcula el IC al 95% de confianza.

prop.test(9476,18930)

## 
##  1-sample proportions test with continuity correction
## 
## data:  9476 out of 18930, null probability 0.5
## X-squared = 0.023296, df = 1, p-value = 0.8787
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
##  0.4934326 0.5077293
## sample estimates:
##         p 
## 0.5005811

Se estima que el la proporción de docentes que recibieron apoyo psicológico está entre 49.3% y 50.8%.

Luego, para responder a la pregunta de si esta proporción varía entre docentes hombres y mujeres, tenemos que crear otra tabla con las frecuencias y porcentajes por cada grupo de la variable “sexo”. Para esto, al código anterior le agregamos el comando group_by.

tabla2 = endo2020 %>%
  filter(apoyo =="Sí" | apoyo == "No") %>%
  group_by(sexo) %>%
  count(Apoyo = apoyo, name="N") %>%
  mutate(total = sum(N), 
         Por = N / total * 100,
         err = sqrt(Por*(100-Por)/N), 
         liminf = Por - 1.96*err, 
         limsup = Por + 1.96*err)
tabla2

## # A tibble: 4 × 8
## # Groups:   sexo [2]
##   sexo   Apoyo     N total   Por   err liminf limsup
##   <fct>  <fct> <int> <int> <dbl> <dbl>  <dbl>  <dbl>
## 1 Hombre Sí     2777  6163  45.1 0.944   43.2   46.9
## 2 Hombre No     3386  6163  54.9 0.855   53.3   56.6
## 3 Mujer  Sí     6699 12767  52.5 0.610   51.3   53.7
## 4 Mujer  No     6068 12767  47.5 0.641   46.3   48.8

El mismo comando prop.test permite hacer la prueba para la diferencia de proporciones. Para esto, los valores tanto de hombres, como de mujeres, se concatenan con la especificación c(…), tanto para el n de “Sí” de cada grupo, como para el total de casos de cada grupo.

prop.test(c(2777, 6699), c(6163,12767))

## 
##  2-sample test for equality of proportions with continuity correction
## 
## data:  c(2777, 6699) out of c(6163, 12767)
## X-squared = 91.044, df = 1, p-value < 2.2e-16
## alternative hypothesis: two.sided
## 95 percent confidence interval:
##  -0.08938432 -0.05885549
## sample estimates:
##    prop 1    prop 2 
## 0.4505922 0.5247121

Según los resultados, se encuentra que el 52.5% de docentes mujeres recibieron apoyo psicológico versus el 45.1% de docentes hombres. Este comando no nos brinda directamente los límites inferior y superior de los IC de cada grupo, pero nos brinda el IC de la diferencia de proporciones al 95% de confianza. Este IC de la diferencia de proporciones varía entre -8.9% y -5.9%.

Como este IC va solo entre valores negativos; es decir, como el IC no incluye al cero, se puede concluir que la diferencia de proporciones no puede ser cero, por lo tanto, que existe una diferencia estadísticamente significativa en las proporciones entre ambos grupos.

La tabla 2 se puede usar para graficar. Como nos interesa comparar los porcentajes de docentes que reportaron haber recibido atención psicológica por sexo, se puede eliminar las filas de aquellos que no recibieron atención psicológica en la tabla 2.

tabla2 = tabla2[-c(2,4),]

Luego, con esta tabla podemos seguir el mismo procedimiento que con el cálculo de las barras de error para la media, pero esta vez para los porcentajes.

library(ggplot2)
graf2 = ggplot(tabla2, aes(x=sexo, y=Por))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=paste(round(Por, 1))), vjust=-1, size=4)+
  xlab("Sexo del docente") + ylab("Porcentaje que recibió atención psicológica")+
  ylim(0, 60)
graf2

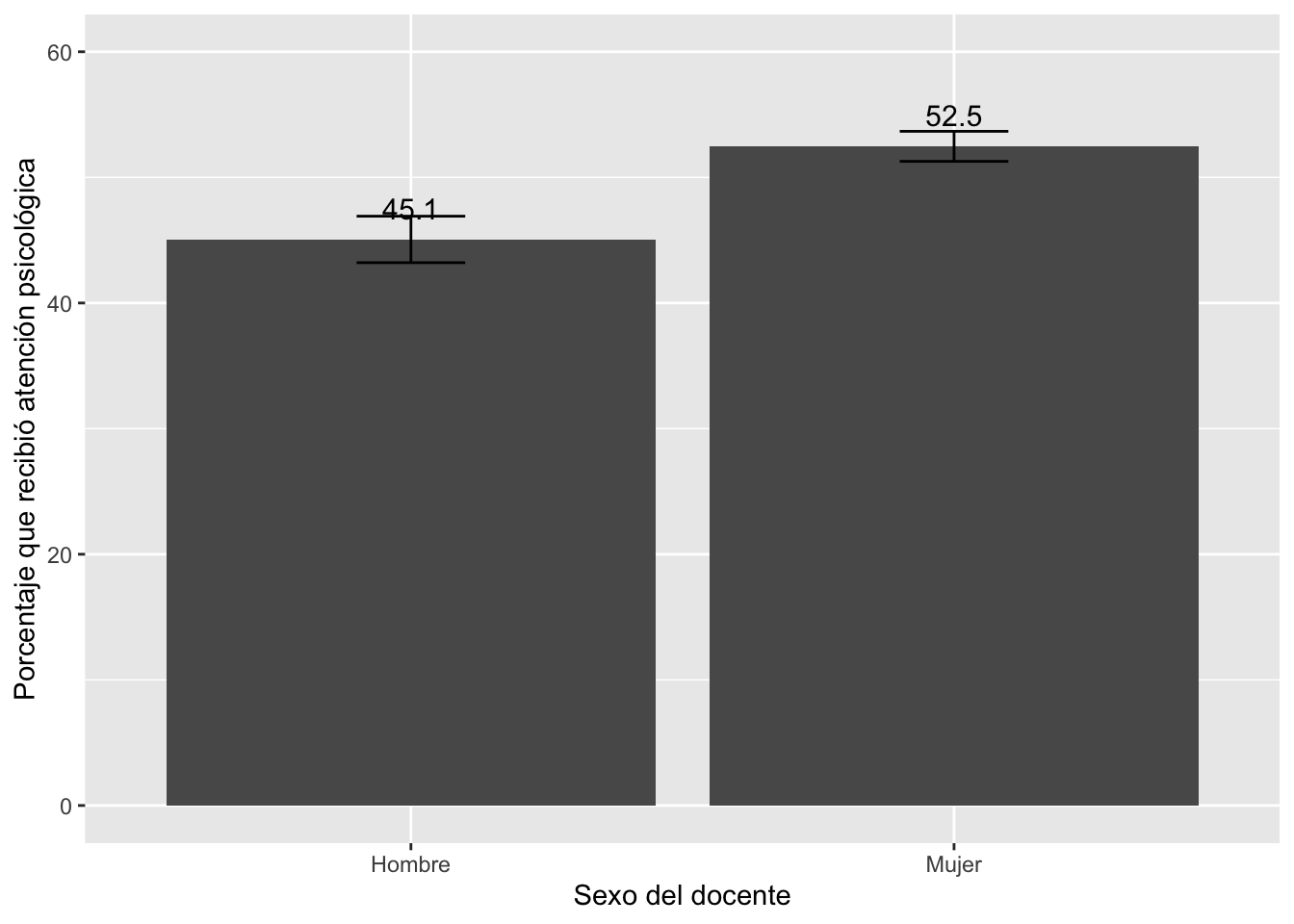
De este gráfico se puede concluir que existen diferencias estadísticamente significativas en el porcentaje de docentes que buscaron atención psicológica entre hombres y mujeres, debido a que los intervalos de confianza no se traslapan.

De manera más específica, se puede afirmar que las docentes peruanas reciben más atención psicológica que los docentes hombres.

Ejemplo 2 para una variable categórica: LAPOP

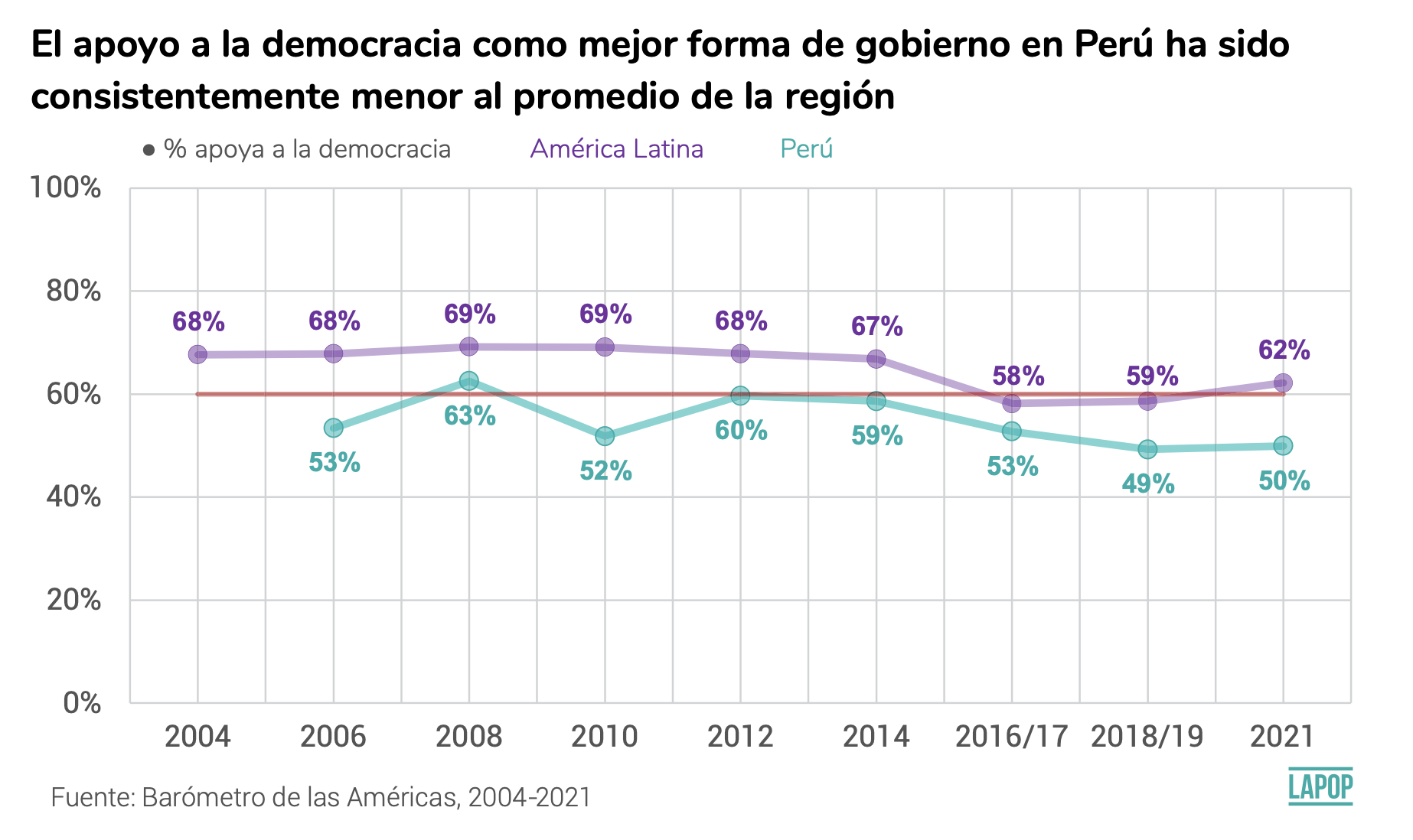
En la página 21 del reporte Cultura política de la democracia en Perú y en las Américas 2021: Tomándole el pulso a la democracia se presenta el gráfico que muestra el porcentaje de apoyo a la democracia en Perú (línea magenta) a lo largo del tiempo, en comparación con América Latina (línea morada).

El apoyo a la democracia, variable “ING4”, está medida en una escala del 1 al 7, donde 1 significa “muy en desacuerdo” y 7 significa “muy de acuerdo”. Esta variable se tiene que recodificar. De acuerdo al reporte “Las respuestas van de 1 (muy en desacuerdo) a 7 (muy de acuerdo). Para este análisis, se codificaron las respuestas en el extremo”de acuerdo” de la escala (valores que van de 5 a 7) como apoyo a la democracia.” (p.7).

Para recodificar la variable se usa el siguiente código. El resultado es una variable dicotómica (0=No, 1=Sí), que es una variable categórica, aunque incluye un grupo que no tiene respuesta en esta variable y está como NAs.

library(dplyr)
lapop = lapop %>%
  mutate(ing4rec= case_when(
    ing4 >= 1 & ing4 <= 4 ~ 0,
    ing4 >= 5 & ing4 <= 7 ~ 1,
    ))

Se verifica la recodificación.

lapop %>%
  count(ing4, name="Frecuencia")

##   ing4 Frecuencia
## 1    1        113
## 2    2        109
## 3    3        191
## 4    4        335
## 5    5        337
## 6    6        200
## 7    7        236
## 8   NA         14

Lo que queremos es encontrar el intervalo de confianza de la proporción (o porcentaje) de aquellos que responden “Sí” (las 7754 personas con un 1). Ojo que la tabla muestra a 393 personas con NAs.

lapop %>%
  count(ing4rec, name="Frecuencia")

##   ing4rec Frecuencia
## 1       0        748
## 2       1        773
## 3      NA         14

Y queremos calcular el porcentaje de aquellos que responden “Sí” por año de la encuesta. La variable que registra el año de la encuesta es “wave”. Esta variable se carga como una numérica (por este motivo, en el gráfico anterior el eje X del gráfico aparece como una variable continua) y se tiene que transformar a una de factor llamada “ronda”.

lapop = lapop %>%
  mutate(ronda = factor(wave))

Se calcula el apoyo a la democracia por años. Para el cálculo de esta tabla queremos excluir a aquellos que no tienen respuesta en la variable apoyo a la democracia (los 393 NAs anteriores). Esto lo podemos hacer con el comando filter, donde especificamos que solo queremos calcular los porcentajes de aquellos que respondieron No (o 0 en la variable) y aquellos que respondieron Sí (o 1 en la variable).

En cada grupo se quiere calcular el intervalo de confianza de la proporción. Recuerden que la fórmula que se tiene que usar es la de intervalos de confianza de la proporción.

Dentro del comando mutate calculamos el total en cada grupo (total), la proporción (Por), el error estándar (err que es igual a la raíz cuadrada del porcentaje por 100-porcentaje entre N) y el límite inferior y superior del intervalo de confianza.

tabla3 = lapop %>%
  filter(ing4rec ==0 | ing4rec == 1) %>%
  group_by(ronda) %>%
  count(Apoyo = ing4rec, name="N") %>%
  mutate(total = sum(N), 
         Por = N / total * 100, 
         err = sqrt(Por*(100-Por)/N), 
         liminf = Por - 1.96*err, 
         limsup = Por + 1.96*err)
tabla3

## # A tibble: 2 × 8
## # Groups:   ronda [1]
##   ronda Apoyo     N total   Por   err liminf limsup
##   <fct> <dbl> <int> <int> <dbl> <dbl>  <dbl>  <dbl>
## 1 2023      0   748  1521  49.2  1.83   45.6   52.8
## 2 2023      1   773  1521  50.8  1.80   47.3   54.3

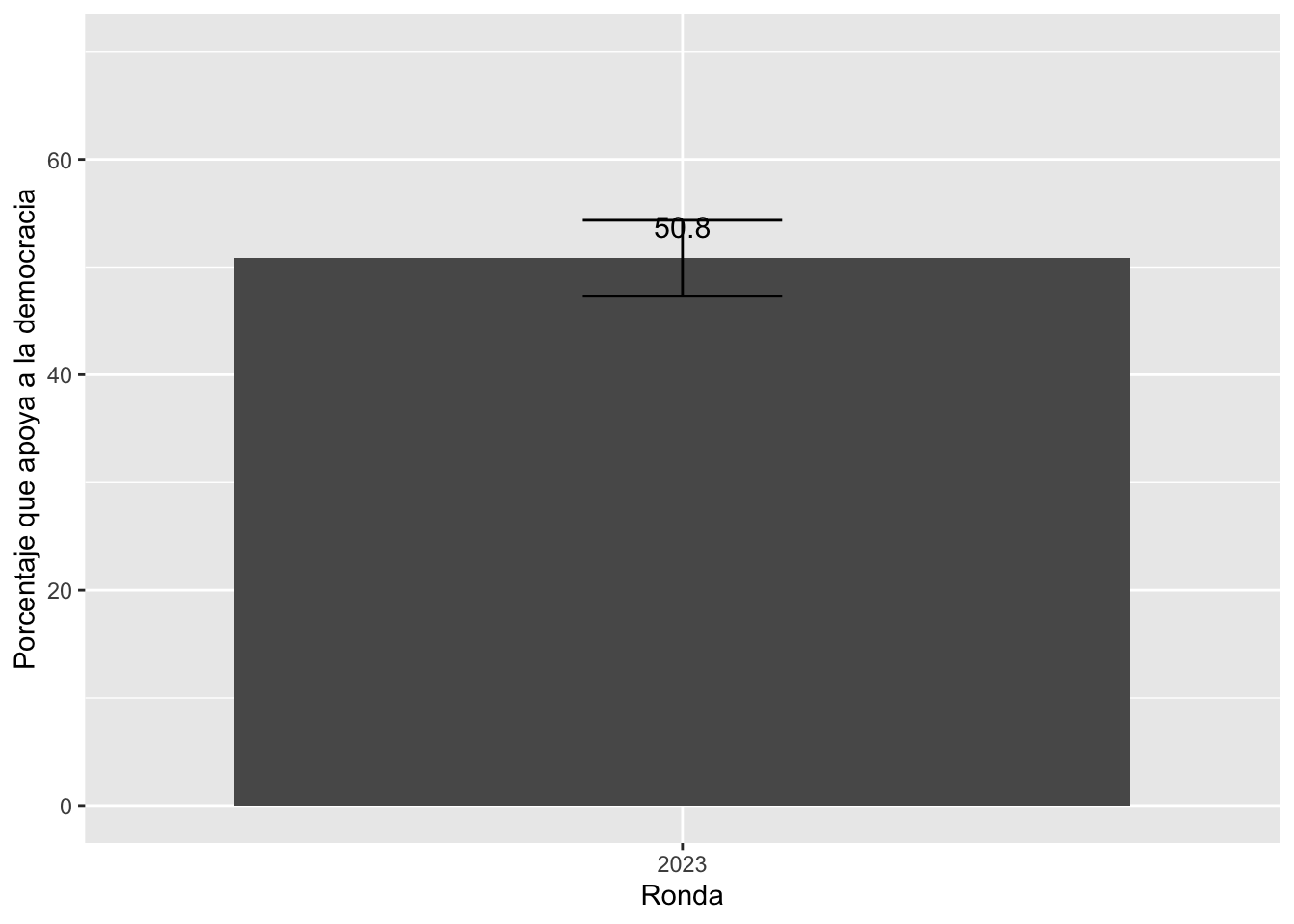
La tabla muestra los datos de los que no apoyan a la democracia (filas donde Apoyo=0) y de los que sí apoyan a la democracia (filas donde Apoyo=1) por cada ronda.

Como solo se quiere graficar a los que sí apoyan a la democracia, se deben eliminar todas las filas impares.

tabla3 = tabla3[-c(1,3,5,7,9,11,13,15),]
tabla3

## # A tibble: 1 × 8
## # Groups:   ronda [1]
##   ronda Apoyo     N total   Por   err liminf limsup
##   <fct> <dbl> <int> <int> <dbl> <dbl>  <dbl>  <dbl>
## 1 2023      1   773  1521  50.8  1.80   47.3   54.3

Ahora, tenemos los datos para graficar.

graf4 = ggplot(tabla3, aes(x=ronda, y=Por))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=liminf, ymax=limsup), width=0.2)+
  geom_text(aes(label=paste(round(Por, 1))), vjust=-1, size=4)+
  xlab("Ronda") + ylab("Porcentaje que apoya a la democracia")+
  ylim(0, 70)
graf4

Nota final

La comparación de IC, ya sea calculando los valores para cada grupo o ya sea de manera gráfica, es una primera manera de analizar si las diferencias entre grupos se pueden extrapolar a la población.

Pero esta es una manera “informal” de hacer esta comparación. Para formalizar esta comparación existe una prueba estadística llamada prueba t de diferencias de medias o la prueba de proporciones, que se verán en la siguiente sesión.

Bibliografía

Galarza, Francisco, Liuba Kogan, and Gustavo Yamada. 2012. “Detectando Discriminación Sexual y Racial En El Mercado Laboral de Lima.” In Chapters of Books, 1:103–35. Fondo Editorial, Universidad del Pacífico.