Clase 1

---

Niveles de medición

---

Variables categóricas

• Variables nominales

  • Individuos:

    • Sexo: Hombre=1, Mujer=2.

      

    • Religión: Católico=1, Evangélico=2, Otro=3.

    

    

    • Algún miembro de su familia se ha contagiado de COVID: Sí=1, No=0.

  

  • Distritos:

    • Departamento: Arequipa=1, Ayacucho=2,…, Ucayali = 24

    • Región: Costa=1, Sierra=2, Selva=3.

    

    • Partido del alcalde: AP=1, APP=2,…., Otro=XX.

    • Alcalde reelegido: Si=1, No=0.

• Variables ordinales

  • Individuos:

    • Educación: Analf=0, Prim=1, Sec=2, Tec=3, Univ=4, Post=5.

    

    • Importancia de religión en su vida: Nada importante=1, Poco importante=2, Algo importante=3, Muy importante=4.

    

    • Gravedad de contagio de COVID: Nada grave=1, Poco grave=2, Algo grave=3, Muy grave=4 (PERO, quién evalúa? percepción?)

  • Distritos:

    • Calidad del servicio de agua: Muy mala=1, Mala=2, Regular=3, Buena=4, Muy buena=5. (PERO, si es percepción, percepción de quién?)

Ambas son llamadas “factor” en R.

---

Variables numéricas

• Continua

  • Individuos:

    • Estatura: en cm o en mt, pero estandarizado.

    • Peso: en kg o en gm, pero estandarizado.

    • Ingreso mensual: en soles. Definir si del individuo o de la familia, si es ingreso mensual o quincenal o anual.

    

  • Distritos:

    • Extensión: en km2

    • PBI per cápita: en soles.

    • Ingreso mensual promedio: en soles.

• Discreta

  • Individuos:

    • Número de hijos: definir si en total o que viven en el hogar.

    • Edad: en años cumplidos. Para más precisión se pide la fecha de nacimiento.

  • Distritos:

    • Número de revocatorias.

    • Número de postas médicas.

    • Población.

Ambas son llamadas “num” en R.

---

Bases de datos

De manera convencional (y así es en R), las bases de datos (o “dataframes” en R) son rectangulares y se organizan en filas y columnas. Cada una de las filas corresponde a una observación (ya sea un individuo, un distrito o la unidad de análisis que se use). Cada columna corresponde a una variable (una característica de la unidad de análisis).

---

Ejemplo 1

• Unidad de análisis: individuos

• Muestra: 10 individuos

• Variables

  • Sexo. 10 observaciones: H, H, M, H, M, M, M, H, M, H

  • Nivel educativo. 10 observaciones: S, S, U, U, P, S, S, P, U, U

  • Edad. 9 observaciones + 1 valor perdido: 25, 54, 37, 65, NA, 73, 48, 32, 51, 37

En formato de base de datos o de “dataframe”:

id	sexo	educ	edad
1	1	2	25
2	1	2	54
3	2	3	37
4	1	3	65
5	2	1	NA
6	2	2	73
7	2	2	48
8	1	1	32
9	2	3	51
10	1	3	37

---

Asumiendo que este dataframe se llama “alumnos”, entonces

• Variable sexo: alumnos$sexo

• Variable educación: alumnos$educ

• Variable edad: alumnos$edad

Ejemplo 2

• Unidad de análisis: distritos del Perú

• Muestra: 1821 distritos

• Variables

  • Región. 1821 observaciones: C, C, C, S, S, Se, C, C, S…….Se

  • Calidad de agua. 1821 observaciones: M, MM, M, MM, R, B……M

  • Número de postas. 1821 observaciones: 2, 1, 0, 0, 2, 3, 1, 0…..0

id	region	agua	posta
1	1	2	2
2	1	1	1
3	1	2	0
…
1821	3	1	0

Si el dataframe se llama “distritos”, entonces:

• Variable región: distritos$region

• Variable agua: distritos$agua

• Variable posta: distritos$posta

Ejemplo 3

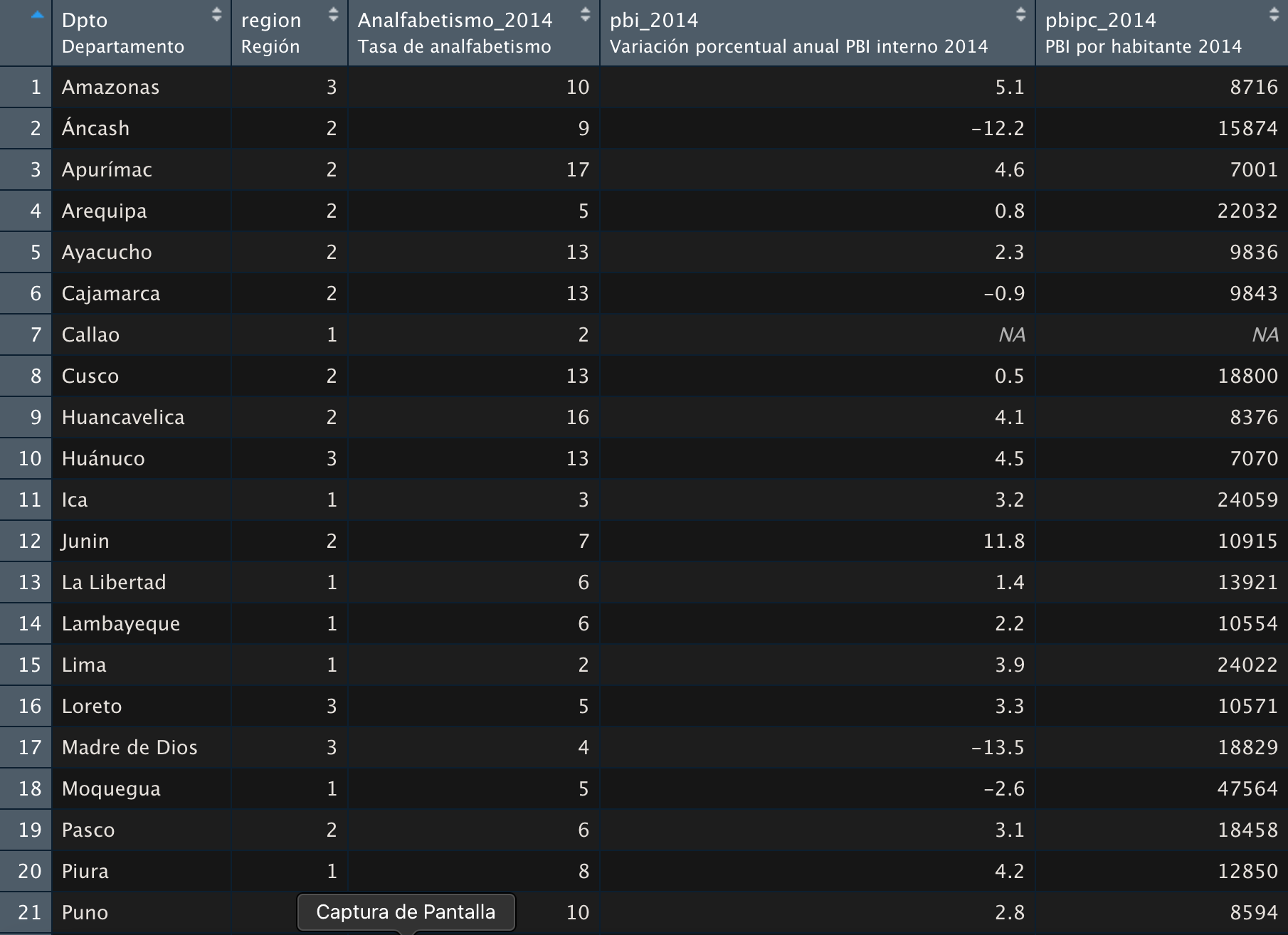
Ejemplo 4

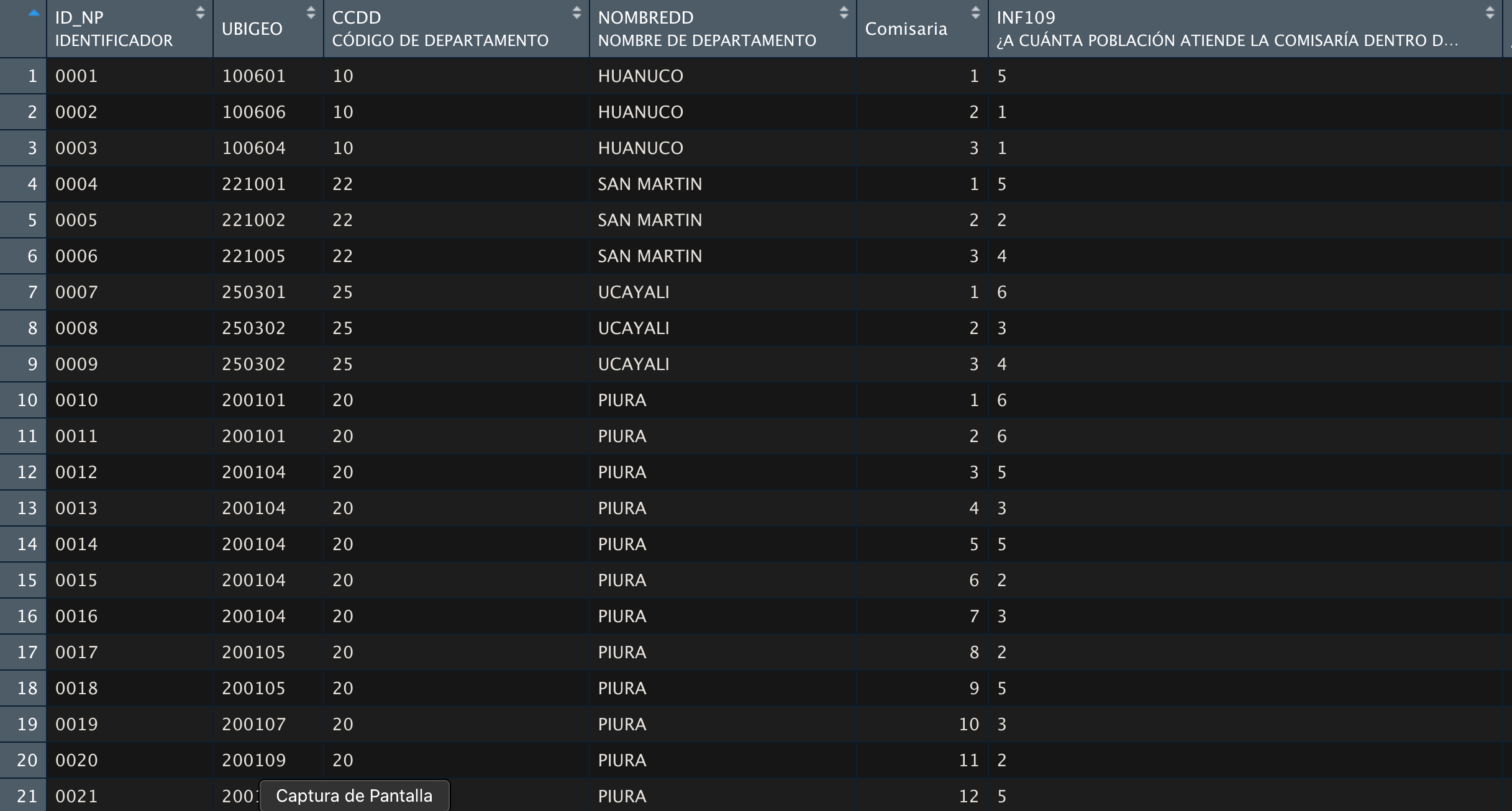
Tarea

Imagínese que quiere crear una base de datos de los alumnos del curso.

1. Proponga un nombre para el dataframe.

2. Proponga 3 variables (una nominal, una ordinal y una numérica), que no sean las sociodemográficas (sexo, edad, educación).

3. Cómo se llamarían estas variables en RStudio? Nombre cada una.