Regresion lineal simple usando datos del Barómetro de las Américas

Introducción

En esta sección veremos los principales aspectos de los modelos de regresión de mínimos cuadrados ordinarios (MICO, en español u ordinary least square, OLS, en inglés). Esta es una extensión del tema de correlación visto en la sección anterior.

En esta sección se replicará los análisis del capítulo “Legitimidad democrática” del reporte El Pulso de la Democracia. En ese capítulo se analiza una medición de apoyo a la democracia.

Sobre la base de datos

Los datos que vamos a usar deben citarse de la siguiente manera: Fuente: Barómetro de las Américas por el Proyecto de Opinión Pública de América Latina (LAPOP), wwww.LapopSurveys.org. Pueden descargar los datos de manera libre aquí.

Se recomienda limpiar el Environment antes de iniciar esta sección. En este documento se carga una base de datos en formato RData. Este formato, nativo de R, es más eficiente en términos de espacio de almacenamiento lo que permite alojarlo en GitHub (que tiene restricciones de tamaño de archivos). Esta base contiene la información de la ronda 2018 para todas las variables. Esta base de datos se encuentra alojada en el repositorio”materials_edu” de la cuenta de LAPOP en GitHub. Mediante la librería rio y el comando import se puede importar esta base de datos desde este repositorio, usando el siguiente código.

library(rio)
#lapop18 <- import("lapop18.RData")
lapop18 <- import("https://raw.github.com/lapop-central/materials_edu/main/lapop18.RData")
lapop18 <- subset(lapop18, pais<=35)

Apoyo al sistema

Como vimos en la sección sobre manejo de datos, para calcular este índice de apoyo al sistema se trabaja con un conjunto de cinco variables:

B1. ¿Hasta qué punto cree usted que los tribunales de justicia de (país) garantizan un juicio justo? \[Sondee: Si usted cree que los tribunales no garantizan para nada la justicia escoja el número 1; si cree que los tribunales garantizan mucho la justicia, escoja el número 7 o escoja un puntaje intermedio\].

B2. ¿Hasta qué punto tiene usted respeto por las instituciones políticas de (país)?

B3. ¿Hasta qué punto cree usted que los derechos básicos del ciudadano están bien protegidos por el sistema político de (país)?

B4. ¿Hasta qué punto se siente orgulloso de vivir bajo el sistema político de (país)?

B6. ¿Hasta qué punto piensa usted que se debe apoyar al sistema político de (país)?

Como indica el reporte “Para cada pregunta, la escala original de 1 (”Nada”) a 7 (“Mucho”) se recodifica en una escala de 0 a 100, de tal forma que 0 indica el menor nivel de apoyo al sistema político y 100 es el nivel máximo de apoyo al sistema político. Esta nueva escala sigue la recodificación típica de LAPOP y puede ser interpretada como una medición del apoyo en unidades, o grados, en una escala continua que va de 0 a 100” (p.34).

Para crear el índice de apoyo a la democracia, se tiene que reescalar cada variable, originalmente medida en una escala de 1-7, a una nueva escala de 0-100.

lapop18$b1rec <- ((lapop18$b1-1)/6)*100
lapop18$b2rec <- ((lapop18$b2-1)/6)*100
lapop18$b3rec <- ((lapop18$b3-1)/6)*100
lapop18$b4rec <- ((lapop18$b4-1)/6)*100
lapop18$b6rec <- ((lapop18$b6-1)/6)*100

Con estas nuevas variables, se calcula la media por cada observación de la base de datos. Esto se puede hacer con el comando rowMeans, donde se indica las columnas que se quiere promediar con la especificación [, 1370:1374]. El promedio de las 5 variables recodificadas se guarda en un nuevo objeto “apoyo”.

Se puede asumir que esta nueva variable es numérica, por lo que se puede describir con el comando summary. El comando summary muestra que esta nueva variable tiene un mínimo de 0 y máximo de 100.

lapop18$apoyo <- rowMeans(lapop18[,1370:1374])
summary(lapop18$apoyo)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    0.00   33.33   50.00   48.79   66.67  100.00    1761

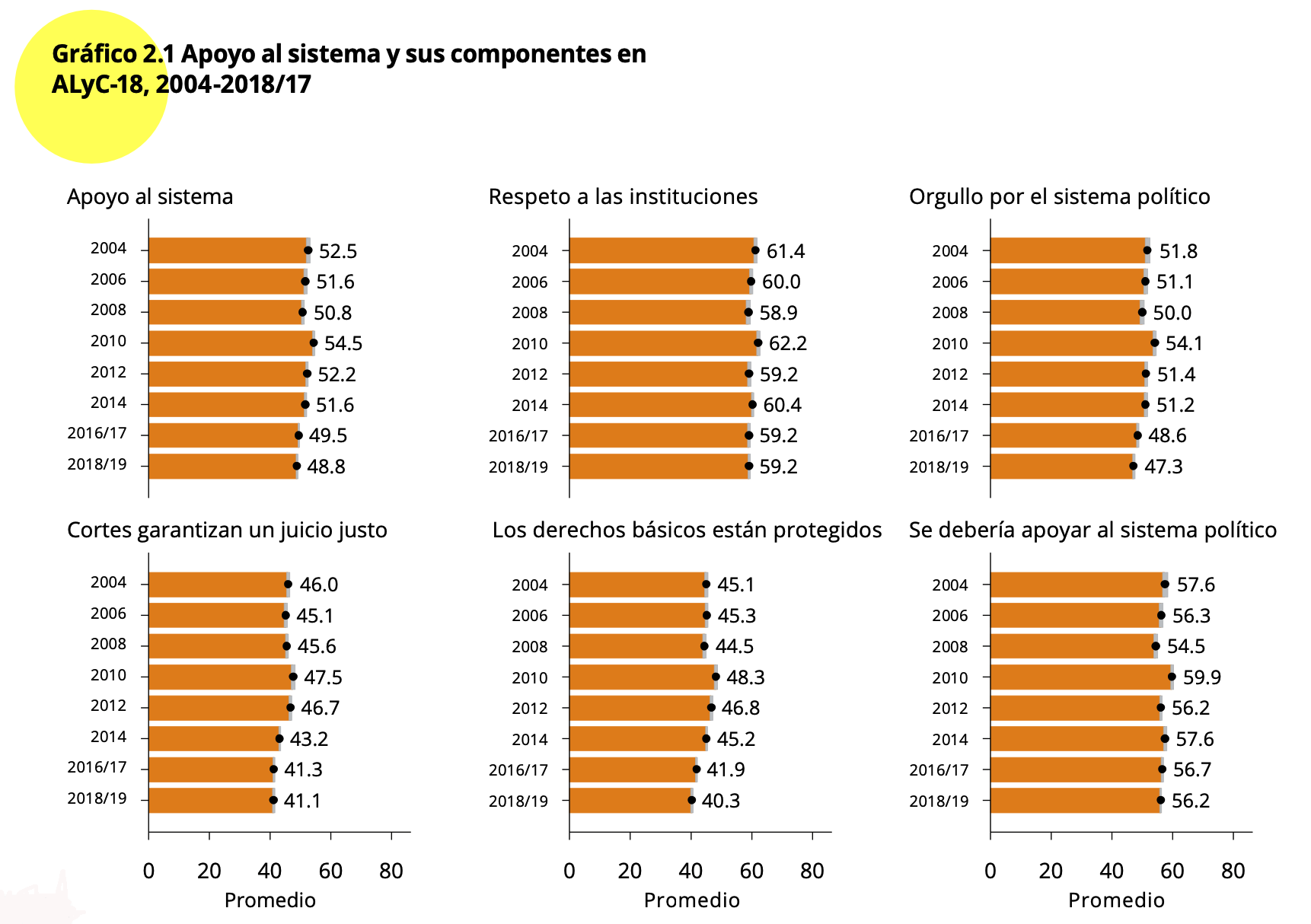
Se comprueba que el promedio reportado es de 48.8 unidades, similar al que aparece en el Gráfico 2.1 para el 2018.

Determinantes de apoyo al sistema

El Gráfico 2.10 muestra la relación entre apoyo al sistema y cinco variables independientes, usadas como predictores de esta variable dependiente. Estas variables son:

• Índice de tolerancia política, construida a partir de cuatro variables: D1, D2, D3 y D4.

• Eficacia externa (EFF1): “A los que gobiernan el país les interesa lo que piensa la gente como usted- ¿Hasta qué punto está de acuerdo o en desacuerdo con esta frase?”.

• Confianza en el ejecutivo (B21A): “¿Hasta qué punto tiene confianza en el presidente/primer ministro?”.

• Confianza en el gobierno local (B32): “¿Hasta qué punto tiene usted confianza en su alcaldía?”.

• Confianza en su comunidad (IT1): “Ahora, hablando de la gente de por aquí, ¿diría que la gente de su comunidad es muy confiable, algo confiable, poco confiable o nada confiable?”.

El gráfico muestra los resultados para estas cinco variables, pero el modelo de regresión incluye controles socioeconómicos y demográficos y efectos fijos por país. Los resultados se presentan en un tipo de gráfico que es común en los reportes del proyecto LAPOP y en la investigación académica.

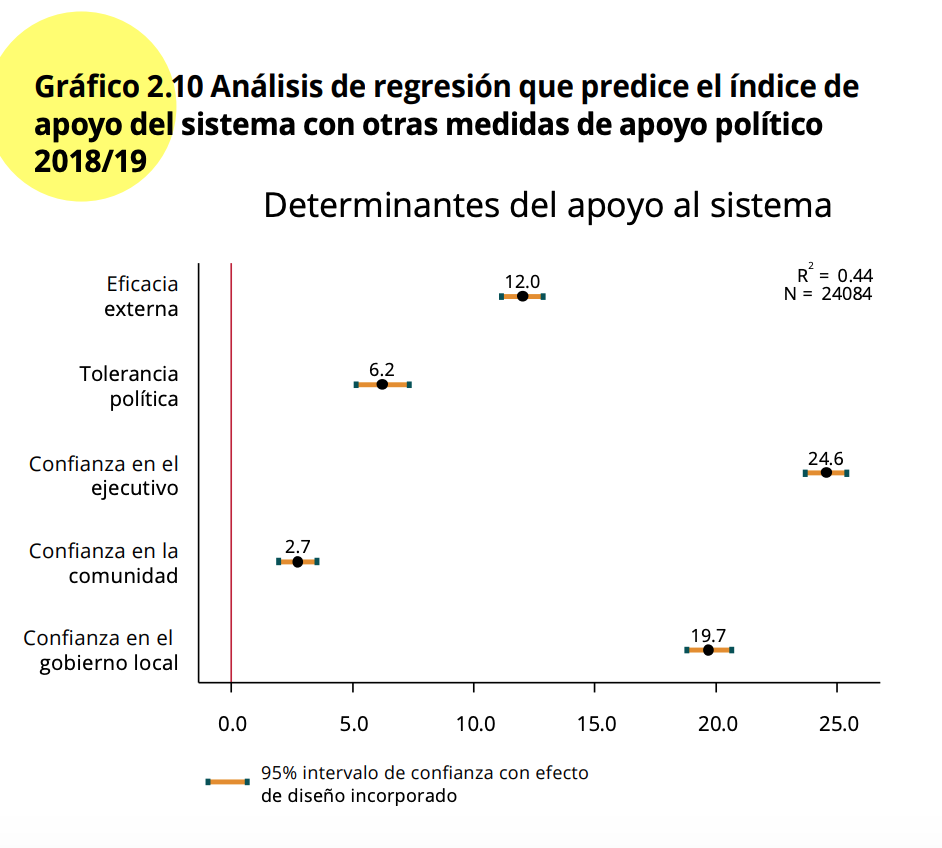
El Gráfico 2.10 muestra los coeficientes de cada variable y el intervalo de confianza al 95% de este estimado. Se incluye una línea vertical en el punto 0. Si un intervalo de confianza cruza esta línea vertical, se puede decir que la variable independiente no tiene una relación estadísticamente significativa con la variable dependiente de apoyo al sistema. Los intervalos de confianza que no cruzan esta línea y que se encuentran a la derecha (izquierda) de esta línea tienen una relación positiva (negativa) con el apoyo al sistema, es decir, cuando aumenta esta variable, el apoyo al sistema promedio aumenta (disminuye). En este ejemplo, las cinco variables son estadísticamente significativas y muestran una relación positiva con el apoyo al sistema.

También se muestra el valor del coeficiente de determinación \(R^2\). Este coeficiente indica la bondad de ajuste de un modelo a la variable dependiente. Mire la proporción de la varianza total de la variable dependiente explicada por el modelo de regresión lineal. Este coeficiente varía entre 0 y 1.

Finalmente el Gráfico 2.10 muestra el N con el que se calcula el modelo. Este N no necesariamente es igual al tamaño de muestra, debido a que los valores perdidos en cualquiera de las variables incluidas en el modelo disminuye este total de observaciones.

Modelo de regresión lineal simple

En primer lugar, empezaremos por la relación entre una variable independiente y una dependiente. Para esto, usaremos el apoyo al sistema como variable dependiente y a la confianza en el ejecutivo como variable independiente. Este es un ejercicio parcial al que se encuentra en el Gráfico 2.10, donde se usan 5 variables independientes como predictores del apoyo al sistema en un modelo de regresión multivariado.

En la sección anterior se calculó la variable dependiente. Luego de calcular la variable dependiente, se procede a calcular la principal variable independiente, la confianza en el ejecutivo. Esta variable es la B21A. ¿Hasta qué punto tiene usted confianza en presidente/primer ministro?. Esta variable está medida en una escala de 1-7 y debe ser recodificada a una escala de 0-100.

lapop18$ejec <- ((lapop18$b21a-1)/6)*100
summary(lapop18$ejec)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    0.00    0.00   50.00   42.88   66.67  100.00     390

Para evaluar la relación entre la variable de confianza en el ejecutivo y el apoyo al sistema se puede calcular un modelo de regresión lineal. El modelo se calcula con el comando lm (de linear model) donde se indica la variable Y y luego la X. Este modelo de guarda en un objeto “modelo1” el que se puede describir con el comando summary.

modelo1 <- lm(apoyo ~ ejec, data=lapop18)
summary(modelo1)

## 
## Call:
## lm(formula = apoyo ~ ejec, data = lapop18)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -68.834 -13.785   1.166  13.707  66.215 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 33.78463    0.19029   177.5   <2e-16 ***
## ejec         0.35049    0.00342   102.5   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 19.7 on 26141 degrees of freedom
##   (1899 observations deleted due to missingness)
## Multiple R-squared:  0.2866, Adjusted R-squared:  0.2866 
## F-statistic: 1.05e+04 on 1 and 26141 DF,  p-value: < 2.2e-16

Estos resultados pueden ser presentados de una manera más formal mediante diferentes comandos. Aquí proponemos usar el comando summ de la librería jtools.

library(jtools)
summ(modelo1)

## MODEL INFO:
## Observations: 26143 (1899 missing obs. deleted)
## Dependent Variable: apoyo
## Type: OLS linear regression 
## 
## MODEL FIT:
## F(1,26141) = 10503.71, p = 0.00
## R² = 0.29
## Adj. R² = 0.29 
## 
## Standard errors: OLS
## ------------------------------------------------
##                      Est.   S.E.   t val.      p
## ----------------- ------- ------ -------- ------
## (Intercept)         33.78   0.19   177.55   0.00
## ejec                 0.35   0.00   102.49   0.00
## ------------------------------------------------

En la información básica del modelo se encuentra que se ha calculado este modelo bivariado sobre 26,143 observaciones. Es decir, del total de observaciones de la base de datos 1,899 se han perdido debido a valores perdidos en alguna de las variables, por lo que esas observaciones no se incluyen en el modelo.

Para evaluar una relación entre dos variables numéricas, tenemos que responder las siguientes preguntas

¿Existe asociación?

La variable confianza en el ejecutivo tiene un coeficiente de 0.35. Los resultados para esta variable muestran además los datos de la prueba de significancia, con el correspondiente p-value. Esta prueba de significancia plantea

\(H0: \beta_1 = 0\)

El p-value se puede interpretar como la probabilidad de observar un coeficiente como el observado (0.35) si el valor del parámetro poblacional fuera cero, que indicaría que no hay relación entre las variables. En nuestro ejemplo bivariado, el p-value encontrado es muy pequeño (2.2e-16). Si planteamos un valor crítico convencional de 0.05, valores de p-value por debajo de este valor nos llevaría a rechazar la H0 y a afirmar que el coeficiente de la variable es diferente de cero, que implica afirmar que existe una relación entre las variables.

Dirección de la relación

El signo del coeficiente nos indica la dirección de la relación. Si el signo es positivo, la relación es positiva entre las variables (a mayor X, mayor Y). Si el signo es negativo, la relación es negativa entre las variables (a mayor X, menor Y).

En nuestro ejemplo bivariado el signo del coeficiente es positivo (aunque está implícito), lo que indica que un aumento en la confianza en el ejecutivo lleva a un aumento promedio en el apoyo al sistema.

Coeficiente de determinación \(R^2\)

El coeficiente de determinación se interpreta como qué tan bien X predice Y y se interpreta como la reducción proporcional en el error al usar la recta de predicción, en lugar de sólo usar \(\bar{Y}\) (el promedio de Y) para predecir Y.

Se tiene que recordar que los errores (o residuos) son las distancias de cada punto a la recta. Cada punto tiene una distancia a la recta de \(\bar{Y}\) y también una distancia a la recta de predicción.

En la imagen de la izquierda, se muestran las distancias de los puntos a la recta de \(\bar{Y}\). Todas estas distancias al cuadrado se pueden sumar. Esta suma es E1.

En la imagen de la derecha, se muestran las distancias de los puntos a la recta de predicción \(\hat{Y}\). Todas estas distancias al cuadrado se pueden sumar. Esa suma es E2.

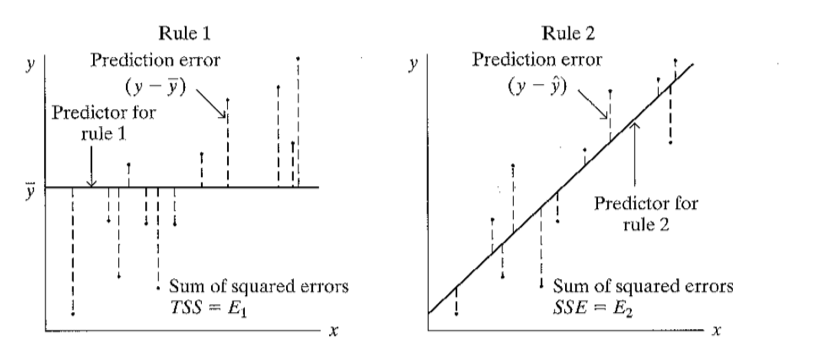
Entonces, \(R^2 = \frac{E1-E2}{E1}\). Este cálculo es igual al cuadrado del valor de la correlación. Por lo tanto:

• \(R^2\) varía entre 0 y 1.

• \(R^2=1\) implica que E2 = 0, es decir que todos los puntos caen en la recta.

• \(R^2=0\) si la pendiente es cero.

En nuestro ejemplo, \(R^2=0.29\). Es decir, el modelo reduce un 29% el error de usar solamente el promedio para estimar Y.

Ecuación de la recta y predicción

Con los datos del modelo se puede construir la ecuación del modelo para valores predichos de la variable dependiente. En nuestro ejemplo tenemos:

\[\hat{Y} = 33.78 + 0.35*X\]

Con esta ecuación se puede calcular el valor predicho de apoyo al sistema para cualquier valor de confianza en el ejecutivo. Por ejemplo, la variable de confianza en el ejecutivo la recodificamos para que varíe entre 0 y 100. De esta manera, se puede calcular que para un valor mínimo de confianza en el ejecutivo (X=0), el apoyo al sistema estimado sería 33.78 puntos. Para un valor máximo de confianza en el ejecutivo (X=100), el apoyo al sistema estimado sería 33.78 + 35 = 68.78 puntos.

Validez del modelo

Los datos de ajuste del modelo también presentan los resultados de una prueba de significancia F. Este test de significancia pone a prueba si los coeficientes en conjunto son iguales a cero. En este caso, esos resultados son iguales a la prueba de significancia del coeficiente de la única variable independiente del modelo.

Esta prueba es más pertinente cuando se analiza un modelo de regresión lineal multivariado. En un análisis multivariado, este test de significancia sería el primer paso en el análisis sobre el modelo en su conjunto.

Resumen

En este documento se ha trabajado un modelo de regresión lineal simple, usando una variable independiente numérica para explicar una variable dependiente numérica. Luego se ha presentado los principales elementos del modelo de regresión lineal simple, como si existe relación, la dirección de la relación, el coeficiente de determinación, la ecuación de la recta y la predicción.

Incluyendo el efecto de diseño

Los cálculos realizados no incluyen el efecto de diseño muestral. Para hacer esto se debe considerar el factor de expansión. Se hizo una introducción al uso del factor de expansión aquí. En este parte usaremos la librería survey.

Usaremos el comando svydesign (similar al comando svyset en STATA). Con este comando se crea un nuevo objeto llamado “lapop.design”, que guarda la información de las variables contenidas en el dataframe, incluyendo en los cálculos el factor de expansión. Por tanto, si luego se creara una nueva variable, se tendría que calcular nuevamente esté comando para que este objeto “lapop.design” incluya esta nueva variable.

library(survey)
lapop.design<-svydesign(ids = ~upm, strata = ~estratopri, weights = ~weight1500, nest=TRUE, data=lapop18)

La librería survey incluye el comando svyglm que permite calcular un modelo de regresión lineal. Las mismas variables usadas en el modelo 1 se pueden incluir en este comando. Se tiene que especificar el diseño que se utiliza y el tratamiento de los valores perdidos. Este cálculo se guarda en un objeto “modelo2”. Se usa el comando summary para describir el modelo.

modelo2 <- svyglm(apoyo~ejec, lapop.design)
summary(modelo2)

## 
## Call:
## svyglm(formula = apoyo ~ ejec, design = lapop.design)
## 
## Survey design:
## svydesign(ids = ~upm, strata = ~estratopri, weights = ~weight1500, 
##     nest = TRUE, data = lapop18)
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 33.780515   0.222170  152.05   <2e-16 ***
## ejec         0.350397   0.003722   94.15   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 389.4621)
## 
## Number of Fisher Scoring iterations: 2

Con el comando summ de la librería jtools se puede presentar el modelo, incluyendo el dato del \(R^2\) ponderado por el factor de expansión.

summ(modelo2)

## MODEL INFO:
## Observations: 26143
## Dependent Variable: apoyo
## Type: Survey-weighted linear regression 
## 
## MODEL FIT:
## R² = 0.29
## Adj. R² = 0.29 
## 
## Standard errors: Robust
## ------------------------------------------------
##                      Est.   S.E.   t val.      p
## ----------------- ------- ------ -------- ------
## (Intercept)         33.78   0.22   152.05   0.00
## ejec                 0.35   0.00    94.15   0.00
## ------------------------------------------------
## 
## Estimated dispersion parameter = 389.46