Intervalos de confianza usando el Barómetro de las Américas

Introducción

En este documento veremos cómo construir intervalos de confianza de la media usando los datos del Barómetro de las Américas. Para eso, vamos a usar los reportes “El pulso de la democracia” de 2018/19, disponible aquí, y de 2021, disponible aquí. En la ronda 2018/19, una de las secciones de este informe, reporta los datos sobre redes sociales y actitudes políticas. En particular, se reporta, en el gráfico 3.9, el grado de satisfacción con la democracia por tipo de usuario de redes sociales. En la ronda 2021, una de las secciones reporta los datos sobre golpes ejecutivos. En el gráfico 1.7 se presenta el porcentaje de ciudadanos que toleran los golpes ejecutivos por país. En ambos casos, los resultados incluyen las estimaciones puntuales y los intervalos de confianza.

Sobre las bases de datos

Los datos que vamos a usar deben citarse de la siguiente manera: Fuente: Barómetro de las Américas por el Proyecto de Opinión Pública de América Latina (LAPOP), wwww.LapopSurveys.org. En este documento se carga una base de datos recortada. Esta base de datos se encuentra alojada en el repositorio “materials_edu” de la cuenta de LAPOP en GitHub. Se recomiendo limpiar el Environment antes de proceder con esta sección.

Mediante la librería rio y el comando import se puede importar esta base de datos desde este repositorio. Además, se seleccionan los datos de países con códigos menores o iguales a 35, es decir, se elimina las observaciones de Estados Unidos y Canadá.

library(rio)
lapop18 = import("https://raw.github.com/lapop-central/materials_edu/main/LAPOP_AB_Merge_2018_v1.0.sav")
lapop18 = subset(lapop18, pais<=35)

También cargamos la base de datos de la ronda 2021.

lapop21 = import("https://raw.github.com/lapop-central/materials_edu/main/lapop21.RData")
lapop21 = subset(lapop21, pais<=35)

Tolerancia a los golpes ejecutivos

El gráfico 1.7 del reporte El pulso de la Democracia para la ronda del Barómetro de las Américas 2021 presenta los resultados del porcentaje de ciudadanos que tolera un golpe ejecutivo. En el gráfico estos datos están representados por la altura de la barra. Este gráfico, además, presente el intervalo de confianza al 95% de este porcentaje en cada país, graficado como una líneas punteadas alrededor de la punto máximo de la barra, que indica el límite inferior y superior del intervalo de confianza.

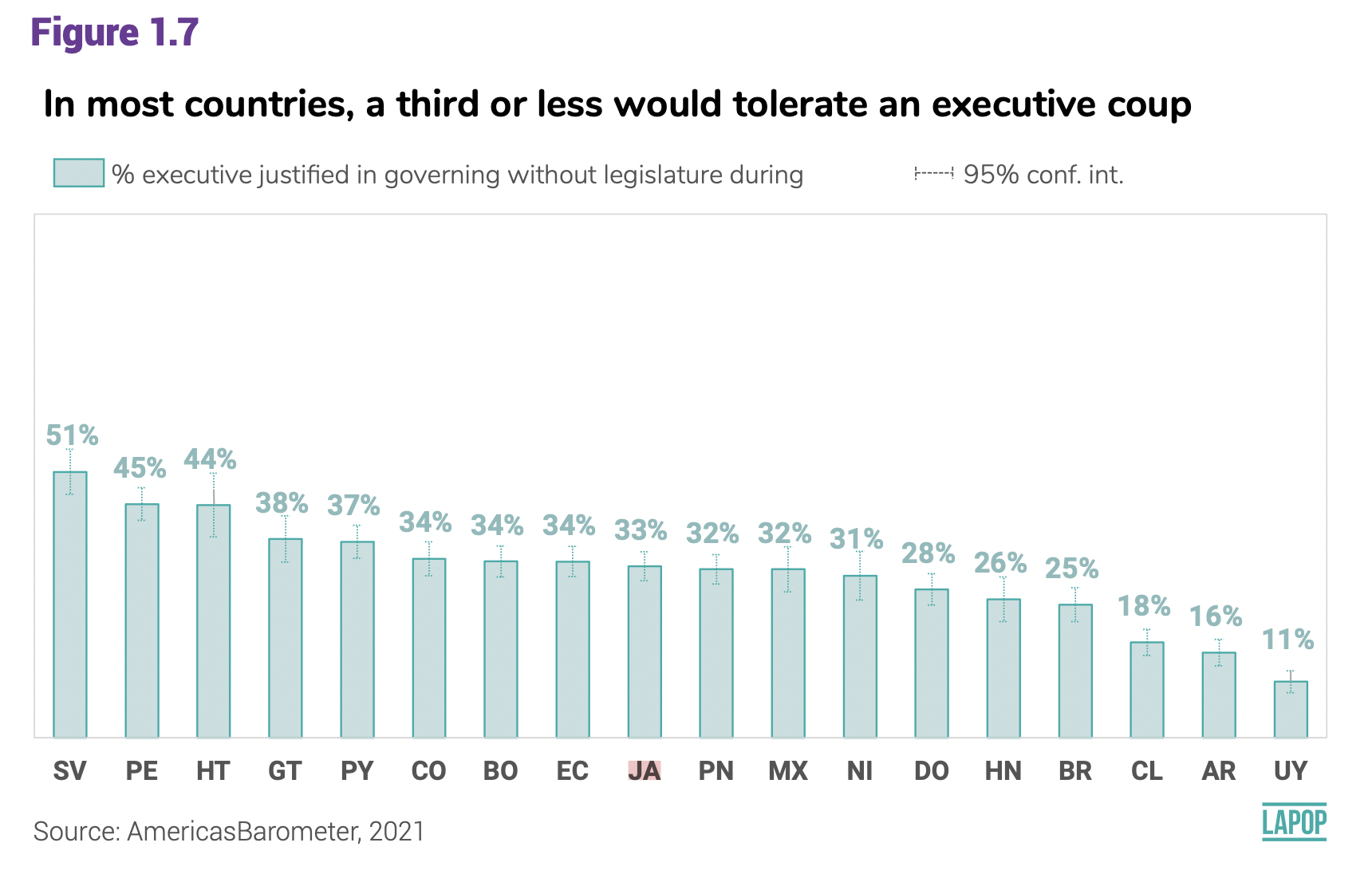
La variable para construir este gráfico es “jc15a” que está fraseada: ¿Cree usted que cuando el país enfrenta momentos muy difíciles, se justifica que el presidente del país cierre el Congreso/Asamblea y gobierno sin Congreso/Asamblea? Las opciones de respuesta son:

1. Sí se justifica
2. No se justifica

Describiendo la tolerancia a los golpes ejecutivos

Para calculas los porcentajes de ciudadanos que justifican o toleran los golpes ejecutivos se tiene que recodificar esta variable, de tal manera que aquellos que justifican tengan el valor 100 y los que no justifican, el valor 0. En este caso se usa el comando recode y se tabula, mediante table, para verificar la recodificación.

lapop21$jc15ar = car::recode(lapop21$jc15a, "1=100; 2=0")
table(lapop21$jc15ar)

## 
##     0   100 
## 14711  5908

Para calcular el porcentaje de ciudadanos que toleran los golpes ejecutivos se puede usar los comandos table y prop.table. La nueva variable “jc15ar” es una variable dummy. En este tipo de variables, la media corresponde a la proporción de respuestas 100. Es decir, si calculamos la media de esta variable, se está calculando el porcentaje para todos los entrevistados. En esta sección vamos a tratar a esta variable como si fuera una variable numérica. En sentido estricto es una variable categórica nominal. Los cálculos de desviaciones estándar y luego de intervalos de confianza, por lo tanto, son referenciales.

El resultado indica que en toda la muestra, el porcentaje de ciudadanos que toleran los golpes ejecutivos es de 28.7%.

summary(lapop21$jc15ar)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    0.00    0.00    0.00   28.65  100.00  100.00   40042

Intervalos de confianza de tolerancia a los golpes ejecutivos

Para calcular el intervalo de confianza al 95% de este porcentaje, se puede usar el comando t.test o la librería lsr, que tiene el comando ciMean. En ambos casos, el resultado nos indica que el porcentaje de ciudadanos que tolera los golpes ejecutivos en la región está entre 28% y 29.3%.

t.test(lapop21$jc15ar)

## 
##  One Sample t-test
## 
## data:  lapop21$jc15ar
## t = 90.996, df = 20618, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  28.03599 29.27038
## sample estimates:
## mean of x 
##  28.65318

library(lsr)
ciMean(as.numeric(lapop21$jc15ar), na.rm=T)

##          2.5%    97.5%
## [1,] 28.03599 29.27038

Tolerancia a los golpes ejecutivos por país

El gráfico 1.7 muestra el porcentaje de ciudadanos que toleran los golpes ejecutivos por país. Para replicar este gráfico, primero tenemos que definir que la variable “pais” es de tipo factor. Se guarda este cambio en una nueva variable “paises”, la que se etiqueta con las siglas de cada país.

lapop21$paises = as.factor(lapop21$pais)
levels(lapop21$paises) = c("MX", "GT", "SV", "HN", "NI", "CR",
                            "PN", "CO", "EC", "BO", "PE",
                            "PY", "CL", "UY", "BR", "AR", "DO",
                            "HT", "JA", "GU")
table(lapop21$paises)

## 
##   MX   GT   SV   HN   NI   CR   PN   CO   EC   BO   PE   PY   CL   UY   BR   AR 
## 2998 3000 3245 2999 2997 2977 3183 3003 3005 3002 3038 3004 2954 3009 3016 3011 
##   DO   HT   JA   GU 
## 3000 3088 3121 3011

Para calcular estos porcentajes por país, se puede usar varias alternativas. Una de las maneras más directas es con la librería Rmisc. Esta librería tiene el comando group.CI, que calcula la media, el límite inferior y superior de una variable por grupos de otra variable. Esta tabla se guarda en un objeto llamado “golpe”. Este comando no incluye las filas de los países donde no hay datos, por lo que no hay filas de Costa Rica ni de Guyana.

library(Rmisc)
golpe = group.CI(jc15ar~paises, lapop21)
golpe

Con esta tabla podemos replicar el gráfico 1.7 con la librería ggplot2. Para incluir los intervalos de confianza se tiene que agregar la especificación geom_errorbar(). La tabla “golpe” tiene el dato de “ymin” en la columna “jc15ar.lower” y el dato de “ymax” en la columna “jc15ar.upper”. Estos datos se deben ingresar en la especificación aes dentro de geom_errorbar. Además, se tiene como opciones width para especificar el ancho de las bigotes de las barras de error, color para especificar el color, cex para especificar el ancho de las líneas y linetype para especificar el tipo de líneas, en este caso puntuadas.

Para poder ordenar las barras de acuerdo al valor de la variable, se puede usar la especificación reorder(grupo, variable) dentro de la especificación aes de ggplot.

library(ggplot2)
graf1 = ggplot(golpe, aes(x=reorder(paises, -jc15ar.mean), y=jc15ar.mean))+
  geom_bar(width=0.5, fill="darkslategray3", colour="#69b3a2", stat="identity")+
  geom_errorbar(aes(ymin=jc15ar.lower, ymax=jc15ar.upper), width=0.4, 
                color="darkcyan", cex=0.4, linetype=3)+
  geom_text(aes(label=paste(round(jc15ar.mean, 1), "%")), vjust=-4.4, size=2.5)+
  xlab("País") + ylab("Tolerancia a golpes ejecutivos (%)")+
  ylim(0, 60)
graf1

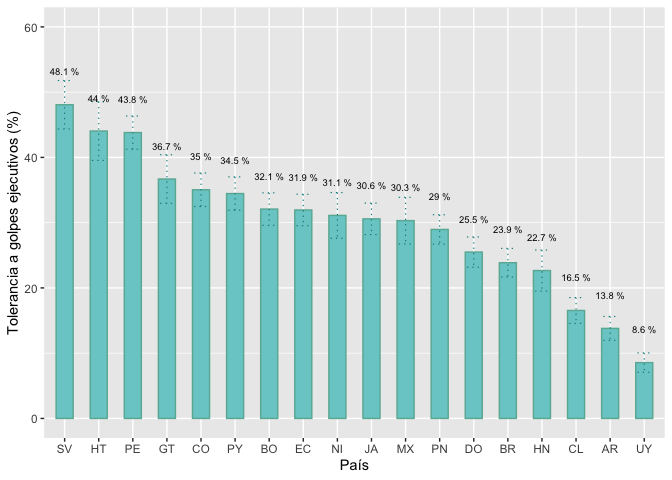
Estos datos, sin embargo, no son exactamente iguales a los presentados en el gráfico 1.7 debido a que estos cálculos no incluyen el efecto de diseño. Más adelante, se verá cómo incluir el efecto de diseño para replicar el gráfico exactamente.

Satisfacción con la democracia

El gráfico 3.9 del reporte El Pulso de la Democracia de la ronda 2018/19 presenta el porcentaje de entrevistados que está satisfecho con la democracia por tipo de usuarios de redes sociales. El porcentaje está marcado como un punto y el intervalo de confianza como un área gris alrededor de estos puntos.

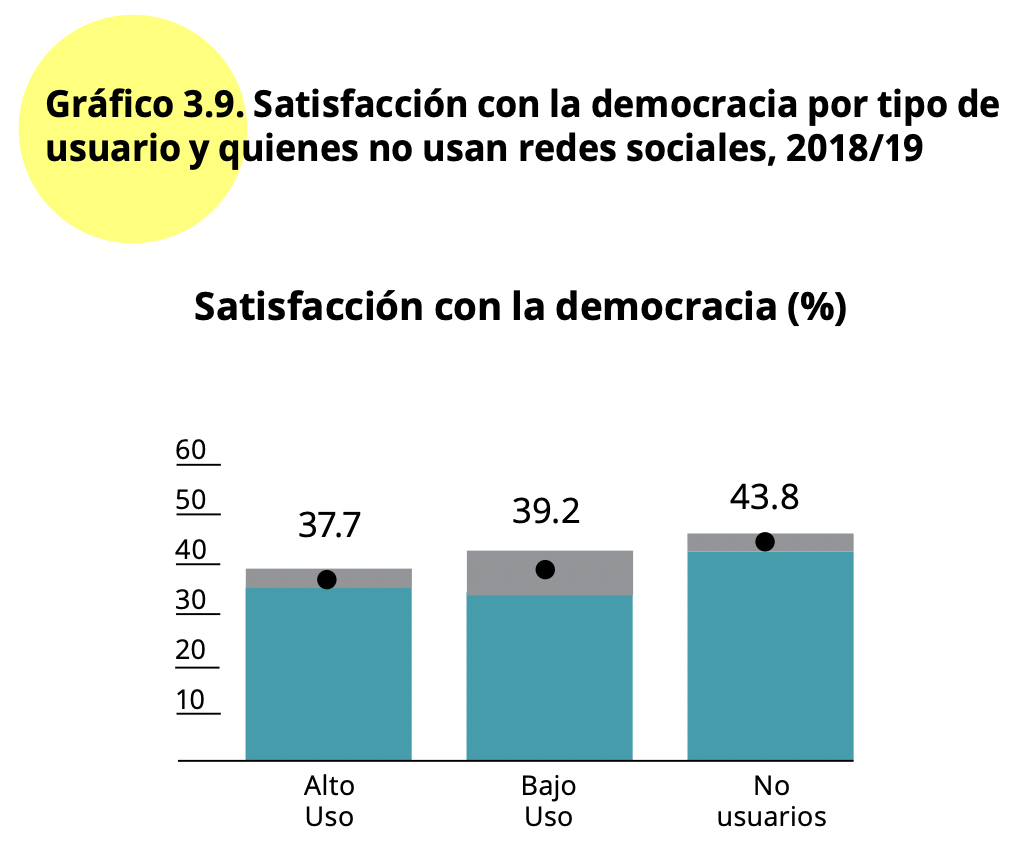
La variable satisfacción con la democracia se llama “pn4” y está codificada de la siguiente manera:

1. Muy satisfecho
2. Satisfecho
3. Insatisfecho
4. Muy insatisfecho

La nota 21 de este reporte indica que “Se codifica a los entrevistados que seleccionan (1) o (2) como satisfechos con la democracia”. Por lo tanto, se tiene que recodificar esta variable. En este caso se usa el comando recode y se tabula, mediante table, para verificar la recodificación.

library(car)
table(lapop18$pn4)

## 
##     1     2     3     4 
##  1727  8916 12455  3855

lapop18$pn4rr = car::recode(lapop18$pn4, "1:2=100; 3:4=0")
table(lapop18$pn4rr)

## 
##     0   100 
## 16310 10643

La nueva variable “pn4rr” es una variable dummy. En este tipo de variables, la media corresponde a la proporción de respuestas 100. Es decir, si calculamos la media de esta variable, se está calculando el porcentaje para todos los entrevistados. En esta sección vamos a tratar a esta variable como si fuera una variable numérica. En sentido estricto es una variable categórica nominal. Los cálculos de desviaciones estándar y luego de intervalos de confianza, por lo tanto, son referenciales.

summary(lapop18$pn4rr)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    0.00    0.00    0.00   39.49  100.00  100.00    1089

Estos resultados muestran una media de 39.5, es decir el 39.5% de los entrevistados están satisfechos con la democracia. Se puede calcular también el intervalo de confianza de esta variable de varias formas. Una primera es mediante la prueba t de una muestra, usando el comando t.test. Otra forma es usando el comando ciMean de la librería lsr.

t.test(lapop18$pn4rr)

## 
##  One Sample t-test
## 
## data:  lapop18$pn4rr
## t = 132.62, df = 26952, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  38.90364 40.07087
## sample estimates:
## mean of x 
##  39.48726

library(lsr)
ciMean(lapop18$pn4rr, na.rm=T)

##          2.5%    97.5%
## [1,] 38.90364 40.07087

Estos resultados indican que el intervalo de confianza de la media de satisfacción con la democracia varía entre 38.9% y 40.1% con 95% de confianza. Se podría cambiar este valor por defecto a 99% de confianza agregando la especificación conf = 0.99 al comando ciMean.

Satisfacción con la democracia por grupos de consumo de información en redes sociales

El informe usa una variable que mide la “exposición frecuente a información política”. Esta variable se construye de una manera compleja, sobre la base de las 3 redes sociales por las que se pregunta. En este caso vamos a empezar con una recodificación más simple para recrear los intervalos de confianza de la variable “satisfacción de la democracia” por grupo de frecuencia de consumo de información de cada red social. Luego se procederá a replicar la variable que se usa en el reporte. La frecuencia de consumo de información (variables “smedia2” para Facebook, “smedia5” para Twitter y “smedia8” para Whatsapp) de cada red social se mide en la siguiente escala:

1. Diariamente
2. Algunas veces a la semana
3. Algunas veces al mes
4. Algunas veces al año
5. Nunca

Vamos a recodificar estas variables de tal manera que aquellos que responden diariamente o algunas veces a la semana serán clasificados como de “alto uso”, aquellos que responden del 3 al 4 serán clasificados como de “bajo uso” y aquellos que responden “nunca” serán clasificados como “no usuarios”. Un esquema similar de clasificación se usa para definir a los usuarios de las 3 redes sociales. Las nuevas variables recodificadas, se convierten a factor y se etiquetan.

table(lapop18$smedia2)

## 
##    1    2    3    4    5 
## 8633 4927 1286  282  231

table(lapop18$smedia5)

## 
##   1   2   3   4   5 
## 795 728 422 193 220

table(lapop18$smedia8)

## 
##     1     2     3     4     5 
## 14151  2646   495    50    87

lapop18$smedia2r = car::recode(lapop18$smedia2, "1:2=1; 3:4=2; 5=3")
lapop18$smedia5r = car::recode(lapop18$smedia5, "1:2=1; 3:4=2; 5=3")
lapop18$smedia8r = car::recode(lapop18$smedia8, "1:2=1; 3:4=2; 5=3")
lapop18$smedia2r = as.factor(lapop18$smedia2r)
lapop18$smedia5r = as.factor(lapop18$smedia5r)
lapop18$smedia8r = as.factor(lapop18$smedia8r)
levels(lapop18$smedia2r) = c("Alto uso", "Bajo uso", "No usuario")
levels(lapop18$smedia5r) = c("Alto uso", "Bajo uso", "No usuario")
levels(lapop18$smedia8r) = c("Alto uso", "Bajo uso", "No usuario")
table(lapop18$smedia2r)

## 
##   Alto uso   Bajo uso No usuario 
##      13560       1568        231

table(lapop18$smedia5r)

## 
##   Alto uso   Bajo uso No usuario 
##       1523        615        220

table(lapop18$smedia8r)

## 
##   Alto uso   Bajo uso No usuario 
##      16797        545         87

Con estas variables recodificadas, se puede calcular las medias (que son los porcentajes) de satisfacción con la democracia por cada grupo de consumo de información en redes sociales.

Una opción que permite mostrar muchos estadísticos por cada grupo es describeBy de la librería psych. El código para Twitter es:

library(psych)
describeBy(lapop18$pn4rr, group=lapop18$smedia5r)

## 
##  Descriptive statistics by group 
## group: Alto uso
##    vars    n  mean    sd median trimmed mad min max range skew kurtosis   se
## X1    1 1505 39.67 48.94      0    37.1   0   0 100   100 0.42    -1.82 1.26
## ------------------------------------------------------------ 
## group: Bajo uso
##    vars   n  mean    sd median trimmed mad min max range skew kurtosis   se
## X1    1 602 37.38 48.42      0   34.23   0   0 100   100 0.52    -1.73 1.97
## ------------------------------------------------------------ 
## group: No usuario
##    vars   n  mean    sd median trimmed mad min max range skew kurtosis   se
## X1    1 213 41.78 49.44      0   39.77   0   0 100   100 0.33     -1.9 3.39

Sin embargo, lo que nos interesa es calcular los intervalos de confianza para cada grupo. En el gráfico 3.9 del reporte se presenta la media de satisfacción con la democracia, mostrado como un punto, y los intervalos de confianza de cada grupo, mostrados como un área gris con límites inferior y superior. Se puede usar la librería Rmisc y el comando group.CI para calcular los intervalos de confianza de la variable satisfacción con la democracia por grupos de consumo de información en Facebook.

library(Rmisc)
group.CI(pn4rr~smedia2r, lapop18)

Con estos datos, por ejemplo, la media de satisfacción con la democracia entre el grupo de alto uso de información en Facebook es 37.6%. El límite inferior del intervalo de confianza es 36.7% y el límite superior es 38.4%. Con estos datos se podría replicar un gráfico de barras similar al 3.9.

Intervalos de confianza de satisfacción con la democracia

La forma más fácil de graficar los intervalos de confianza por grupos es usando el comando plotmeans.

library(gplots)
plotmeans(lapop18$pn4rr~lapop18$smedia5r,
          xlab="Tipo de usuario de Twitter",
          ylab="Satisfacción con la democracia",
          ylim=c(0, 50),
          mean.labels=T, digits=1,
          connect=F
         )

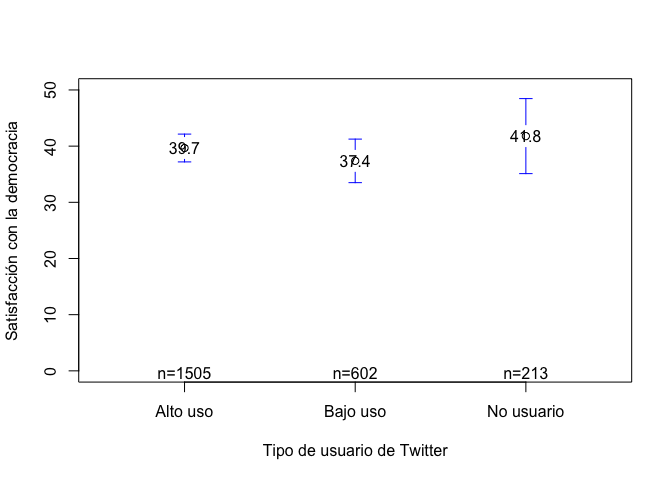
Esta opción muestra los intervalos de confianza pero se dificulta si se quiere graficar las barras. La librería ggplot nos brinda más opciones y nos permite graficar de manera similar al gráfico 3.9 del reporte, en barras, presentar los intervalos de confianza y agregar color. Para esto, primero se guarda un dataframe “tw.uso” con los datos de la media y los límites superior e inferior de cada grupo, usando el comando group.CI. Son los datos de este dataframe los que se usan con ggplot y se crea un gráfico que se guarda en un objeto “graf1”. Con esta librería se agrega la capa geom_bar() para definir que se quiere un gráfico de barras de las variables especificadas en aes. Luego, se agrega la capa geom_errorbar() para agregar las barras de error y luego los valores de la media con geom_text(). Finalmente, se etiqueta el eje X y Y con xlab y ylab y se define los límites del eje Y con ylim.

tw.uso = group.CI(pn4rr~smedia5r, lapop18)
library(ggplot2)
graf2 = ggplot(tw.uso, aes(x=smedia5r, y=pn4rr.mean))+
  geom_bar(width=0.5, fill="darkcyan", colour="black", stat="identity")+
  geom_errorbar(aes(ymin=pn4rr.lower, ymax=pn4rr.upper), width=0.2)+
  geom_text(aes(label=paste(round(pn4rr.mean, 1), "%")), vjust=-4.2, size=4)+
  xlab("Tipo de usuario de Twitter") + ylab("Satisfacción con la democracia (%)")+
  ylim(0, 50)
graf2

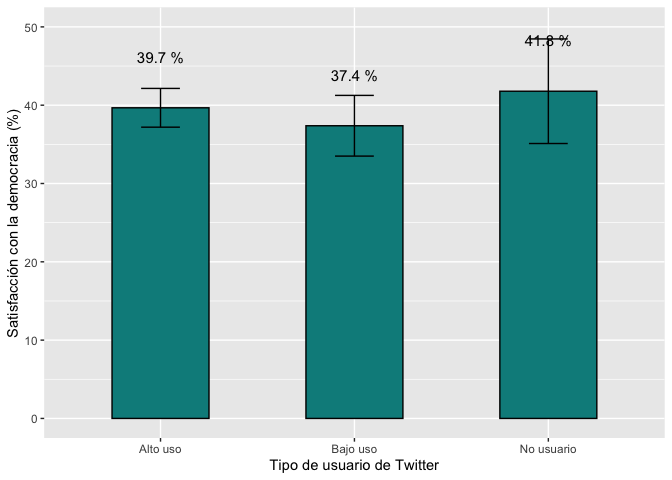
Según estos resultados, la satisfacción con la democracia es más alta en aquellos que no son usuarios de Twitter, en comparación con los usuarios, aunque las diferencias no son estadísticamente significativas de una comparación visual entre los intervalos de confianza.

Satisfacción con la democracia por tipo de usuario de redes sociales

Hasta el momento se ha creado intervalos de confianza de satisfacción con la democracia por tipo de usuarios de Twitter. El reporte agrega a los usuarios de las tres redes sociales para ubicar tres tipos de usuarios: usuarios de alto uso, de bajo uso y no usuarios de cualquier red social. La forma de codificación de este tipo de usuarios de tres redes sociales se basa en varias condiciones. Como dice el reporte: “Usamos la misma codificación que en la anterior sección, para distinguir entre quienes acceden con frecuencia en redes sociales (aquellos con cuentas a las que acceden algunas veces a la semana o a diario) y aquellos que no acceden a las redes sociales muy frecuentemente (aquellos con cuentas a las que acceden algunas veces al mes o algunas veces al año). También incluimos a quienes no son usuarios: quienes no tienen ninguna cuenta en redes sociales (quienes indican que no tienen una cuenta en Facebook, Twitter o Whatsapp) y quienes tienen una cuenta, pero nunca la usan” (p.81). En primer lugar identificamos a quienes usan cada red social algunas veces a la semana o a diario como 1 y si usan cada red social algunas veces al mes o algunas veces al año, como 0. Para esto usamos el comando ifelse. Luego, sumamos los valores de cada red social en una sola variable, con valores entre 0 y 3. Se usa el comando rowSums que permite la suma horizontal de variables definidas, en este caso las que están en la posición [, 89:91]. En este comando, usamos la especificación na.rm=T para que la suma no tome en cuenta a los valores perdidos.

lapop18$sm2 = ifelse(lapop18$smedia2==1 | lapop18$smedia2==2, 1, 0)
lapop18$sm5 = ifelse(lapop18$smedia5==1 | lapop18$smedia5==2, 1, 0)
lapop18$sm8 = ifelse(lapop18$smedia8==1 | lapop18$smedia8==2, 1, 0)
lapop18$anyhi = rowSums(lapop18[,89:91], na.rm=T)
table(lapop18$anyhi)

## 
##     0     1     2     3 
##  9831  5811 11131  1269

Partiendo de esta variable, se crea una variable que agrega las tres redes sociales, llamada “hi_lo_non”. Primero, se crea esta variable como un vector de NAs. Luego se le imputa valores de 1, 2, 3 o NA, dependiendo de los valores de “anyhi o de los valores de las variables de redes sociales. Luego se crea una nueva variable de tipo factor, con idénticos valores que”hi_lo_non” y se etiqueta. La definición de la condicionalidad se trabaja mediante los corchetes [...]. De esta manera, se define las condiciones de la siguiente manera:

• La variable “hi_lo_non es igual a 1 si la variable anyhi es mayor o igual a 1 (uso diario o algunas veces a la semana) = lapop18$hi_lo_non[lapop18$anyhi>=1] <- 1

• La variable “hi_lo_non es igual a 2 si la variable anyhi es igual a 0 (uso algunas veces al año o nunca) = lapop18$hi_lo_non[lapop18$anyhi==0] <- 2

• La variable “hi_lo_non es igual a 3 si las variables de tenencia de cuentas son igual a 2 (No) = lapop18$hi_lo_non[lapop18$smedia1==2 & lapop18$smedia4==2 & lapop18$smedia7==2] <- 3

Las siguiente reglas de codificación siguen la misma lógica de combinación de otras variables para imputar el valor 3 o NA.

lapop18$hi_lo_non = NA #se crea un vector con NAs#
lapop18$hi_lo_non[lapop18$anyhi>=1] = 1 #Se codifica 1 a los que usan diariamente o algunas veces a la semana alguna red social#
lapop18$hi_lo_non[lapop18$anyhi==0] = 2 #Se codifica como 2 a los que usan algunas veces al mes y al año alguna red social#
lapop18$hi_lo_non[lapop18$smedia1==2 & lapop18$smedia4==2 & lapop18$smedia7==2] = 3 #Se codifica como 3 a los que no tiene redes sociales#
lapop18$hi_lo_non[lapop18$smedia2==5 & lapop18$smedia5==5 & lapop18$smedia8==5] = 3 #Se codifica como 3 a los que nunca usan ninguna red social#
lapop18$hi_lo_non[lapop18$pais==3 & (lapop18$smedia2==5 | lapop18$smedia5==5 | lapop18$smedia8==5)] = 3 #Se aplica un código particular a pais 3#
lapop18$hi_lo_non[lapop18$pais==3 & (lapop18$smedia1==2 | lapop18$smedia4==2 | lapop18$smedia7==2)] = 3 #Se aplica un código particular a pais 3#
lapop18$hilon = as.factor(lapop18$hi_lo_non)
levels(lapop18$hilon) = c("Alto uso", "Bajo uso", "No usuario")
prop.table(table(lapop18$hilon))*100

## 
##   Alto uso   Bajo uso No usuario 
##  64.941873   3.480494  31.577634

Según estos datos, el 64.9% de entrevistados reportan un alto uso de redes sociales, mientras que, en el otro extremo, se tiene 31.6% que serían no usuarios de ninguna red social. Estos datos difieren un poco de los reportados en el Apéndice al reporte, disponible aquí, donde se reporte 65.34% de alto uso y 31.60% de no usuarios. Estas diferencias pueden ser debidas a diferencias en la interpretación de las reglas de codificación desde Stata a R.

De la misma forma que se produjo el gráfico de media de satisfacción con la democracia por tipos de usuarios de Twitter usando ggplot, ahora se hará lo mismo pero para los usuarios de las tres redes sociales, variable “hilon”.

library(Rmisc)
satis.uso = group.CI(pn4rr~hilon, lapop18)
library(ggplot2)
graf3.9 = ggplot(satis.uso, aes(x=hilon, y=pn4rr.mean))+
  geom_bar(width=0.5, fill="darkcyan", colour="black", stat="identity")+
  geom_errorbar(aes(ymin=pn4rr.lower, ymax=pn4rr.upper), width=0.2)+
  geom_text(aes(label=paste(round(pn4rr.mean, 1), "%")), vjust=-2.5, size=4)+
  xlab("Tipo de usuario de redes sociales") + ylab("Satisfacción con la democracia (%)")+
  ylim(0, 50)
graf3.9

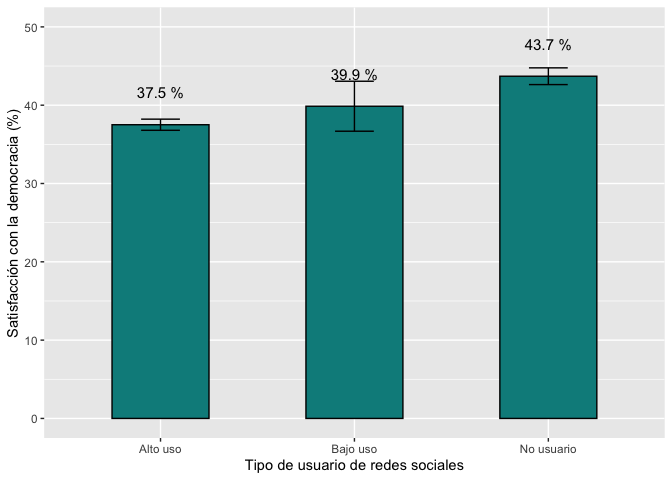
Este gráfico sería una reproducción del que se presenta en el informe (Gráfico 3.9 en la página 62), con una mínimas diferencias por codificación de los datos resultantes.

Resumen

En este documento se ha trabajado con una variable recodificada dummy (satisfacción con la democracia), la que puede ser trabajada como variable numérica para el cálculo de intervalos de confianza de proporciones. Con esta variable se ha calculado el intervalo de confianza de la media, que sería el de la proporción de entrevistados que están satisfechos con la democracia. Luego, se ha descrito esta variables por grupos de una variable de factor (consumo de información política). Se ha presentado cómo calcular los intervalos de confianza de la variable numérica por grupos de la variable de factor. Finalmente, se ha presentado cómo graficar los intervalos de confianza por grupos.

Cálculos incluyendo el efecto de diseño

Resultados de tolerancia a los golpes ejecutivos ponderados

Como se mencionó, los resultados obtenidos acerca de la tolerancia de los golpes ejecutivos, gráfico 1.7 del reporte El Pulso de la Democracia 2021, no son iguales a los obtenidos aquí. Esto es debido a que los cálculos de más arriba no incluye el efecto de diseño.

Para poder realizar los cálculos tomando en cuenta el efecto de diseño, se puede usar la librería survey para definir el diseño muestral. Primero, se tiene que adecuar la base de datos, eliminando los valores perdidos de las variables que definen el diseño muestral (como “weight1500”). Un paso adicional es transformar las variables del dataframe. Esto es debido a que cuando se importan, el sistema lee las variables como tipo “haven_labelled”, es decir, mantiene las etiquetas de las variables, con lo que se podría producir un libro de códigos. Esto es útil en otras ocasiones, pero genera problemas con la librería survey. Para esto transformamos las variables a otro tipo con el comando sapply.

Con la base de datos adecuada, se puede definir el diseño muestra y se guarda en un objeto “diseno21”.

library(survey)
diseno21 = svydesign(ids = ~upm, strata = ~strata, weights = ~weight1500, nest=TRUE, data=lapop21)

La librería survey tiene comandos nativos para calcular la media de la variable recodificada de tolerancia a los golpes ejecutivos. Este cálculo de la media nos brinda el porcentaje de ciudadanos en la región que son tolerantes a los golpes ejecutivos.

svymean(~jc15ar, diseno21, na.rm=T)

##          mean     SE
## jc15ar 30.391 0.3926

Para calcular el intervalo de confianza de esta medida se puede anidar el comando svymean dentro de otro comando confint que nos brinda el límite inferior y superior del intervalo de confianza.

confint(svymean(~jc15ar, diseno21, na.rm=T))

##           2.5 %  97.5 %
## jc15ar 29.62125 31.1601

Para poder replicar el gráfico 1.7 requerimos el valor del porcentaje de ciudadanos que toleran los golpes ejecutivos por páis, así como el intervalo de confianza de cada uno. Para este cálculo, podemos usar el comando svyby. Este comando requiere definir la variable a ser calculada (~jc15ar), la variable que define los grupos (~paises), el objeto que guarda el diseño muestral (diseno21), el estadístico que se quiere calcular (svymean, na.rm=T) y definir el intervalo de confianza (vartype = "ci"). Estos cálculos se guardan en un objeto “golpepond”.

golpepond = svyby(~jc15ar, ~paises, diseno21, svymean, na.rm=T, vartype = "ci")
golpepond = golpepond[-c(6,20),]

De la misma manera que con el gráfico con los resultados no poderados, usamos la librería ggplot para replicar el gráfico 1.7. Se debe tomar en cuenta que el comando svybar genera columnas con nombre diferentes a los que se generan con el comando group.CI usado más arriba.

graf3 = ggplot(golpepond, aes(x=reorder(paises, -jc15ar), y=jc15ar))+
  geom_bar(width=0.5, fill="darkslategray3", colour="#69b3a2", stat="identity")+
  geom_errorbar(aes(ymin=ci_l, ymax=ci_u), width=0.2, color="darkcyan",
                cex=0.4, linetype=3)+
  geom_text(aes(label=paste(round(jc15ar, 0), "%")), vjust=-4.4, size=2.5)+
  xlab("País") + ylab("Tolerancia a golpes ejecutivos (%)")+
  ylim(0, 60)
graf3

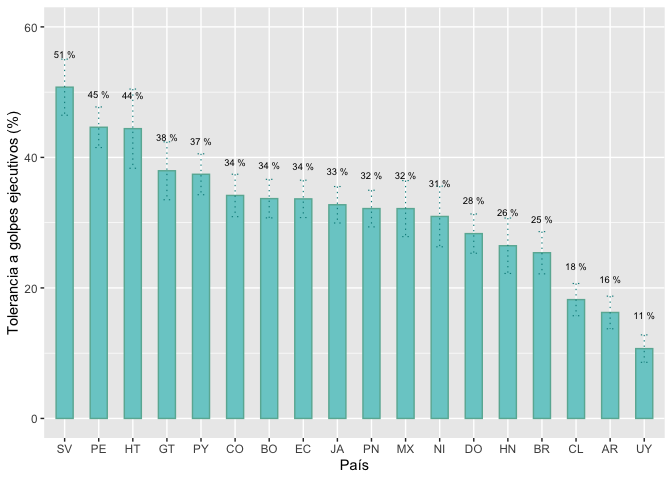
De esta manera se ha replicado exactamente los resultados reportados en El Pulso de la Democracia 2021.

Resultados de satisfacción con la democracia ponderados

De la misma manera que con la tolerancia a los golpes ejecutivos, se usa la librería survey y el comando confintjunto al comando nativo svymean.

library(survey)
diseno18 = svydesign(ids = ~upm, strata = ~estratopri, weights = ~weight1500, nest=TRUE, data=lapop18)

Se puede describir la variable de satisfacción con la democracia incorporando el factor de diseño usando el comando svymean.

svymean(~pn4rr, diseno18, na.rm=T)

##         mean     SE
## pn4rr 39.459 0.3317

Para calcular el intervalo de confianza, se tiene que anidar el código anterior dentro del comando confint. Este comando calcula el intervalo de confianza al 95% por defecto. Se podría cambiar este valor por defecto a 99% de confianza agregando la especificación conf = 0.99 al comando.

confint(svymean(~pn4rr, diseno18, na.rm=T))

##          2.5 %   97.5 %
## pn4rr 38.80884 40.10901

También se puede calcular la media y el intervalo de confianza de satisfacción con la democracia incorporando el efecto de diseño usando el comando svyby. Dentro de este comando se especifica la variable numérica a ser descrita (~pn4rr), la variable que forma los grupos (~smedia5r), el diseño muestral (diseno18), la función que se quiere calcular (svymean), que no tome en cuenta los valores perdidos (na.rm=T) y que incluya el intervalo de confianza de cada grupo (vartype="ci").

tw.uso.weighted = svyby(~pn4rr, ~smedia5r, diseno18, svymean, na.rm=T, vartype = "ci")
tw.uso.weighted

Para poder graficar, estos cálculos se guardan en un dataframe “tw.uso.weighted”, que incluye los datos de la media por cada grupo y el límite inferior y superior del intervalo de confianza. De la misma manera que con los datos que no incluyen el efecto de diseño, se usa la librería ggplot y se crea un gráfico que se guarda en un objeto “graf2”. Se usan especificaciones muy similares a los ejemplos anteriores.

graf4 = ggplot(tw.uso.weighted, aes(x=smedia5r, y=pn4rr))+
  geom_bar(width=0.5, fill="darkcyan", colour="black", stat="identity")+
  geom_errorbar(aes(ymin=ci_l, ymax=ci_u), width=0.2)+
  geom_text(aes(label=paste(round(pn4rr, 1), "%")), vjust=-4.2, size=4)+
  xlab("Tipo de usuario de Twitter") + ylab("Satisfacción con la democracia (%)")+
  ylim(0, 50)
graf4

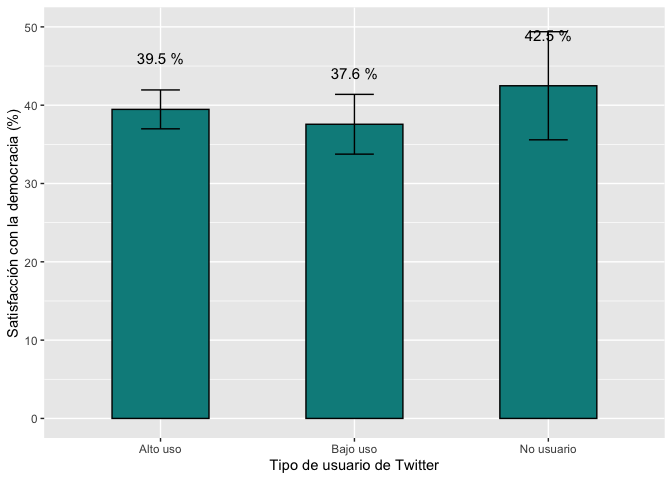
Estos resultados incluyen el efecto de diseño, pero no son exactamente iguales a los reportados en el gráfico 3.9 del reporte El Pulso de la Democracia de la ronda 2018/19 debido a que el cálculo de la variable que define al tipo de usuario de Twitter es más complejo de lo que se hace en esta sección.