Descriptive statistics using the AmericasBarometer (1)

Introduction

In this section we will start with the basics of how to use the LAPOP AmericasBarometer dataset for statistical purposes. First, we will look at the basics of how to describe a variable using a frequency distribution table and how to graph that variable using pie or bar charts. For that, we are going to use the latest regional report “The pulse of democracy”, available here, where the main findings of the 2018/19 round of the AmericasBarometer are presented. One of the sections of this document, reports data on social networks and political attitudes. In this section, data on the use of the internet and the use of social networks are presented, in general and by country. With the data from the AmericasBarometer, it is possible to know the percentage of households with cell phone access, with internet access, as well as the percentage of people who use WhatsApp, Facebook or Twitter. In this document we are going to reproduce these results.

About the dataset

The data that we are going to use should be cited as follows: Source: AmericasBarometer by the Latin American Public Opinion Project (LAPOP), wwww.LapopSurveys.org. In this document a trimmed dataset is reloaded from scratch. It is recommended again to clean the Environment of the objects used in previous modules.

This dataset is hosted in the “materials_edu” repository of LAPOP’s GitHub account. Using the library rio and the commandimport, this dataset can be imported from this repository. In addition, the data for countries with codes less than or equal to 35 are selected, it means that observations for the United States and Canada are eliminated.

library(rio)
lapop18 = import("https://raw.github.com/lapop-central/materials_edu/main/LAPOP_AB_Merge_2018_v1.0.sav")
lapop18 = subset(lapop18, pais<=35)

We also load the 2021 round dataset.

lapop21 = import("https://raw.github.com/lapop-central/materials_edu/main/lapop21.RData")
lapop21 = subset(lapop21, pais<=35)

Support for democracy

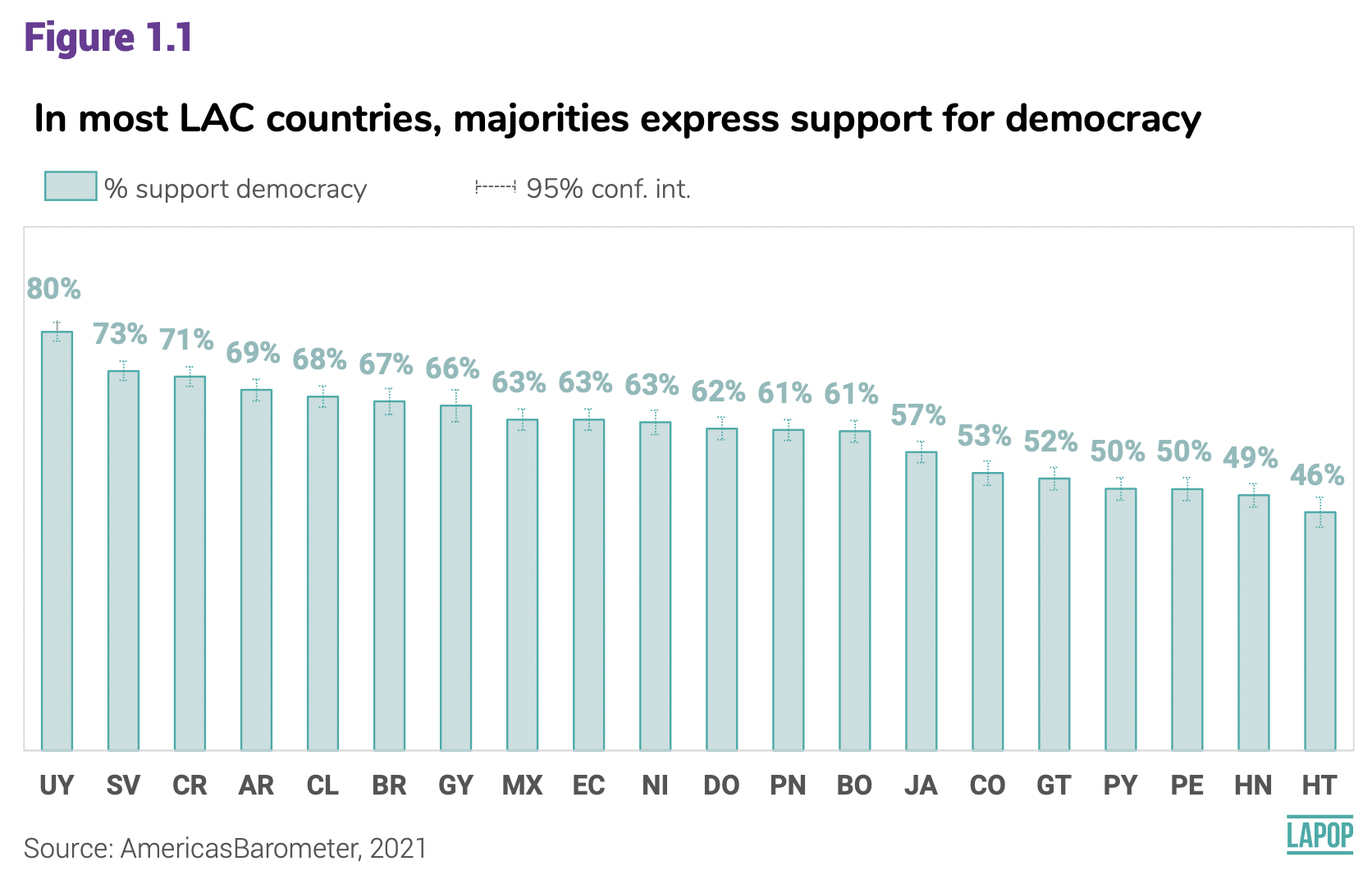
The report The Pulse of Democracy 2021 shows the results for support for democracy by country. Figure 1.1 shows the percentage of people who support democracy in abstract in each country.

In a previous section, we explain how to recode variable ING4, originally measured in a 1-7 scale, where 1 means “Strongly diesagree” and 7 means “Strongly agree”. Values between 5 and 7 are recoded as “1” and this value identifies those who support democracy. The rest are recoded as “0”, those who do not support democracy. The new recoded variable are saved in a new variable “ing4rec”.

library(car)
lapop21$ing4rec = car::recode(lapop21$ing4, "1:4=0; 5:7=1")

In strict sense, this variable is not numeric even though it is defined as “dbl” in the dataset, which is a type of numeric variable. This variable is qualitative, nominal, that is defined as factor in R. For correctly defined and labelled, we have to transform this variable. First, we have to define as factor with the command as.factor.

lapop21$ing4rec = as.factor(lapop21$ing4rec)

A factor variable can have levels for each numeric value. The definition of levels has the goal that tables of figures do not show numeric codes, but the corresponding label. We can do this using the command levels. Then, we can describe this variable with the command table that gives absolute frequencies for each category of this variable.

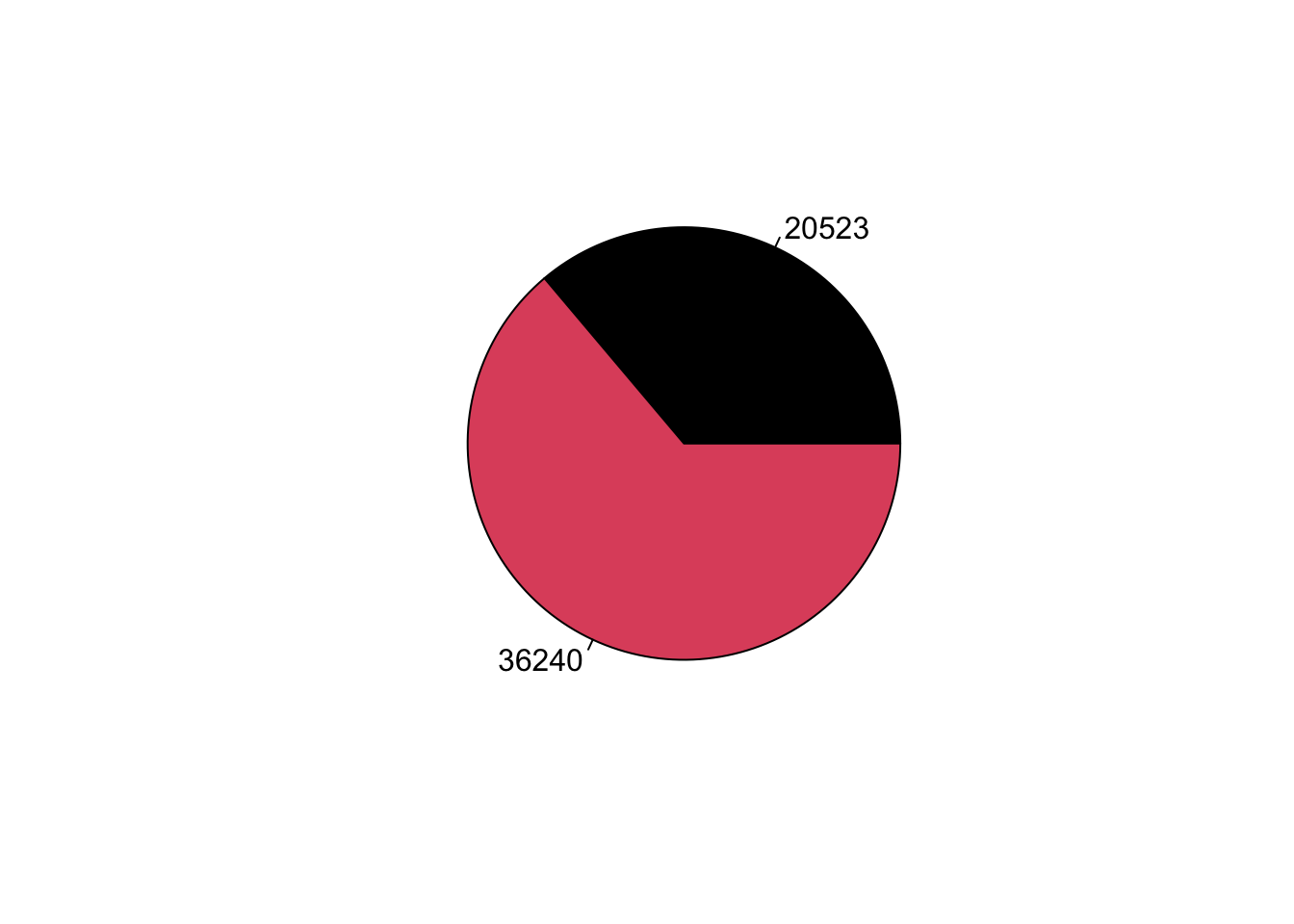
levels(lapop21$ing4rec) = c("No", "Yes")
table(lapop21$ing4rec)

## 
##    No   Yes 
## 20523 36240

Describe variables

As we see in the section Manipulation, we can use the command prop.table to obtain relative frequencies and the command round to show just one decimal.

round(prop.table(table(lapop21$ing4rec))*100, 1)

## 
##   No  Yes 
## 36.2 63.8

Results show two categories in the variable “support for democracy”. However, this variable has missing values. For getting a table showing missing values, we can use the command table with the specification useNA = "always".

round(prop.table(table(lapop21$ing4rec, useNA = "always"))*100, 1)

## 
##   No  Yes <NA> 
## 33.8 59.7  6.4

This table shows that we have 6.4% of missing cases of the total observations. The presentation of missing values in tables or figures depends of the researcher.

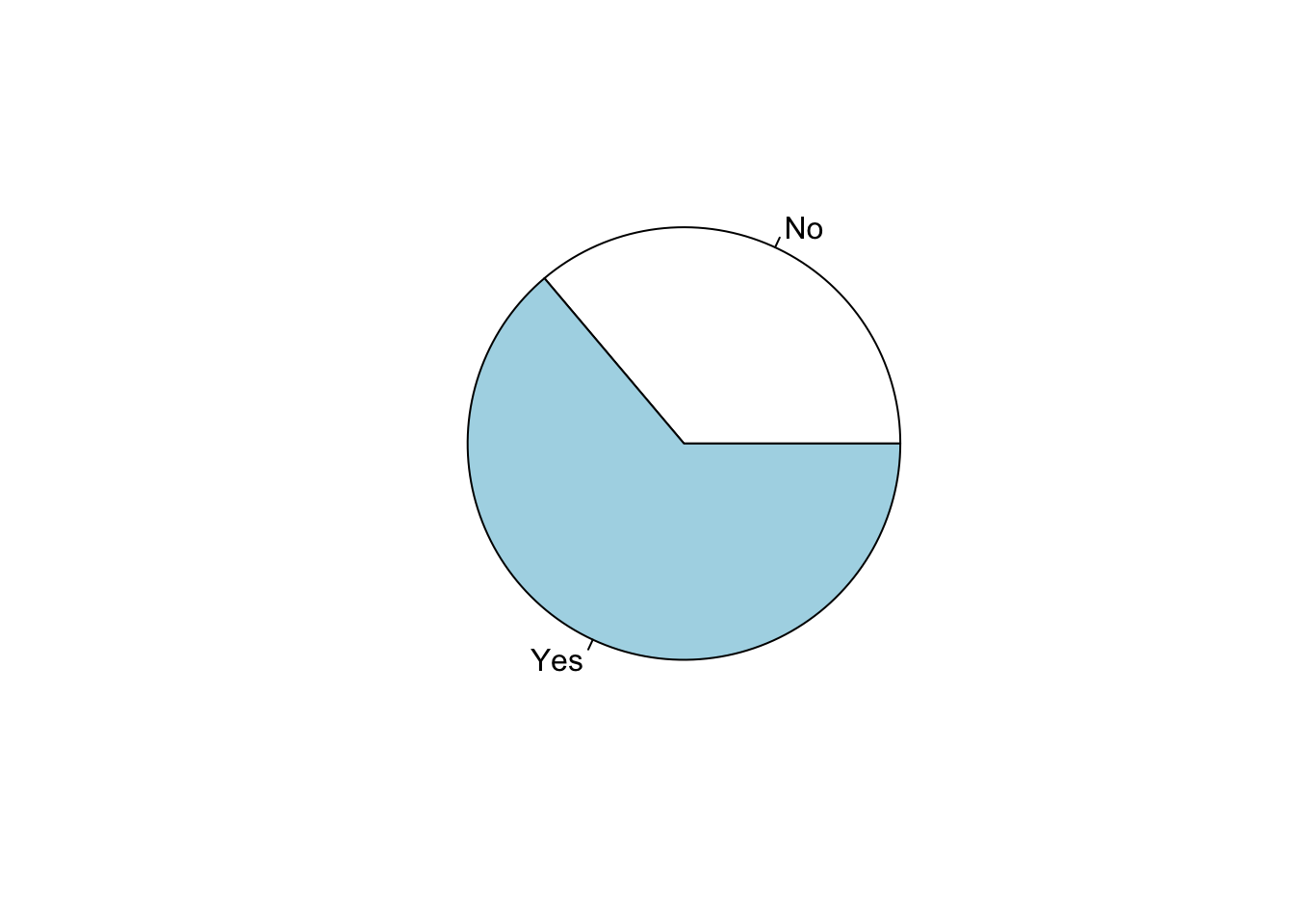
Plot a variable

We can plot a variable of type “factor” in multiple ways. A possibility is by a circular graph. We can use the command pie, which is part of the basic syntax of R. Within this command, we can nest the command table to plot values of a contingency table.

pie(table(lapop21$ing4rec))

This figure has some option to customization. For example, the specification labels = … serves to include the number of observation in each sector, and the specification col =… works to define colors of sectors.

pie(table(lapop21$ing4rec), labels=table(lapop21$ing4rec), col=1:2)

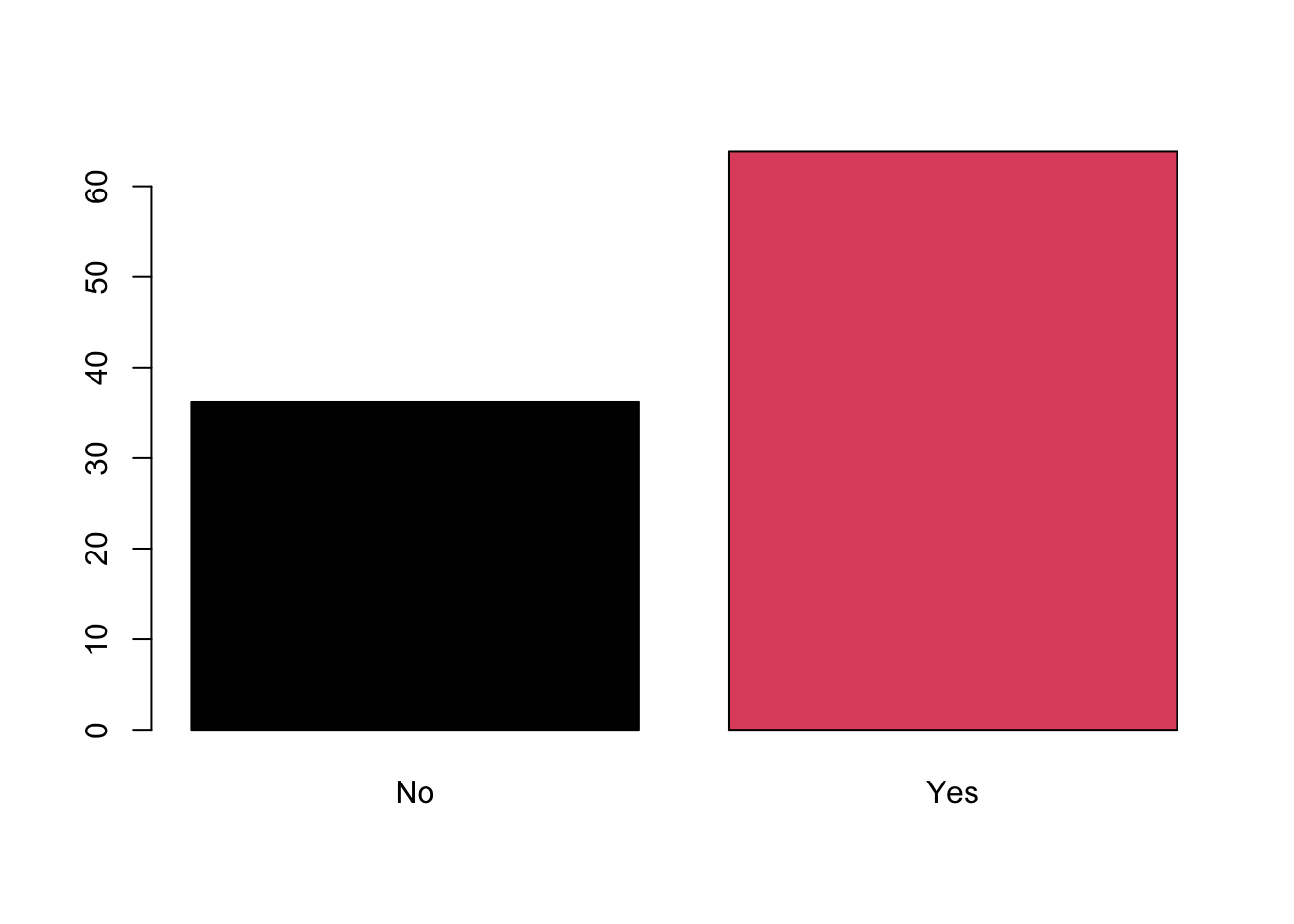
Other option is using a bar plot. Using the basic command of R, we can use barplot. We nest the commands table and prop.table within barplot.

barplot(prop.table(table(lapop21$ing4rec))*100, col=1:2)

The base commands in R have a level of customization, but we have a specialized library to produce a graph with more customization options called ggplot. For example, to reproduce a bar plot of the variable support for democracy, we call the library ggplot2.

In this example, we have to define the basic specification within the command ggplot. This command works by layers. First, we specify the data to be used with data=lapop. Then, the specification aes defines the aesthetic of the plot. Generally, it is used to indicate what variables are plotted in what axis (x or y). In this case, we are working with the data from scratch, from the original dataset “lapop21”. This option obliges to “calculate” the percentages within the specification aes with y =..prop..*100. Also, we should use the specification fill = to define that bars should present a percentage.

Other easier option is to create before a table from the original data that captures percentages and to use this table in the specification aes. Below, we present examples using this option.

After the specification of data and axis, we have to define the type of plot we want to use. We do this with geometries (“geom”). We define a basic bar plot using the command geom_bar( ), where we define internally the width of bars. With the specification labs we define the labels of axis and the “caption”. Finally, with the specification coord_cartesian we define limits for x axis from 0 to 80.

library(ggplot2)
ggplot(data=lapop21, aes(x=ing4rec))+
  geom_bar(aes(y=..prop..*100, group=1), width=0.5)+
  labs(x="Support for democracy", y="Percentage", 
       caption="AmericasBarometer by LAPOP, 2021")+
  coord_cartesian(ylim=c(0, 80))

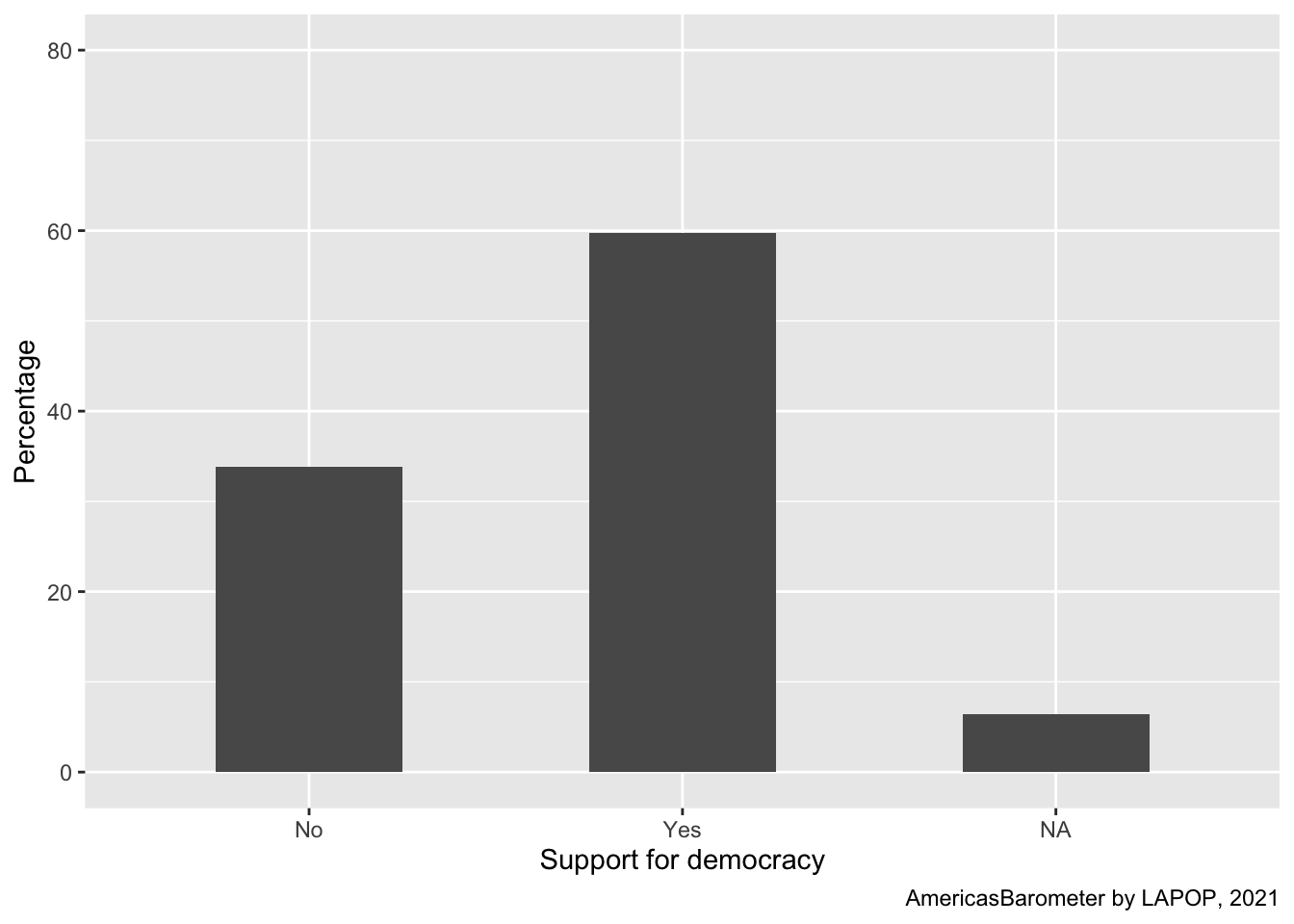
As we say, this plot presents a bar for the percentage of missing values. If a researcher would like to present a plot with percentages of valid cases, missing values should be dropped. We can use the command subset again, but within ggplot for the command (internally) works with the variable no considering the missing values. The syntax !is.na( ) makes the command to not include missing values of a variable in calculations. If we would have used !is.na( ) out of ggplot, we would have dropped all observations with missing values in the dataset, decreasing the N and affecting next calculations.

ggplot(data=subset(lapop21, !is.na(ing4rec)), aes(x=ing4rec))+
  geom_bar(aes(y=..prop..*100, group=1), width=0.5)+
  labs(x="Support for democracy", y="Percentage", 
       caption="AmericasBarometer by LAPOP, 2021")+
  coord_cartesian(ylim=c(0, 80))

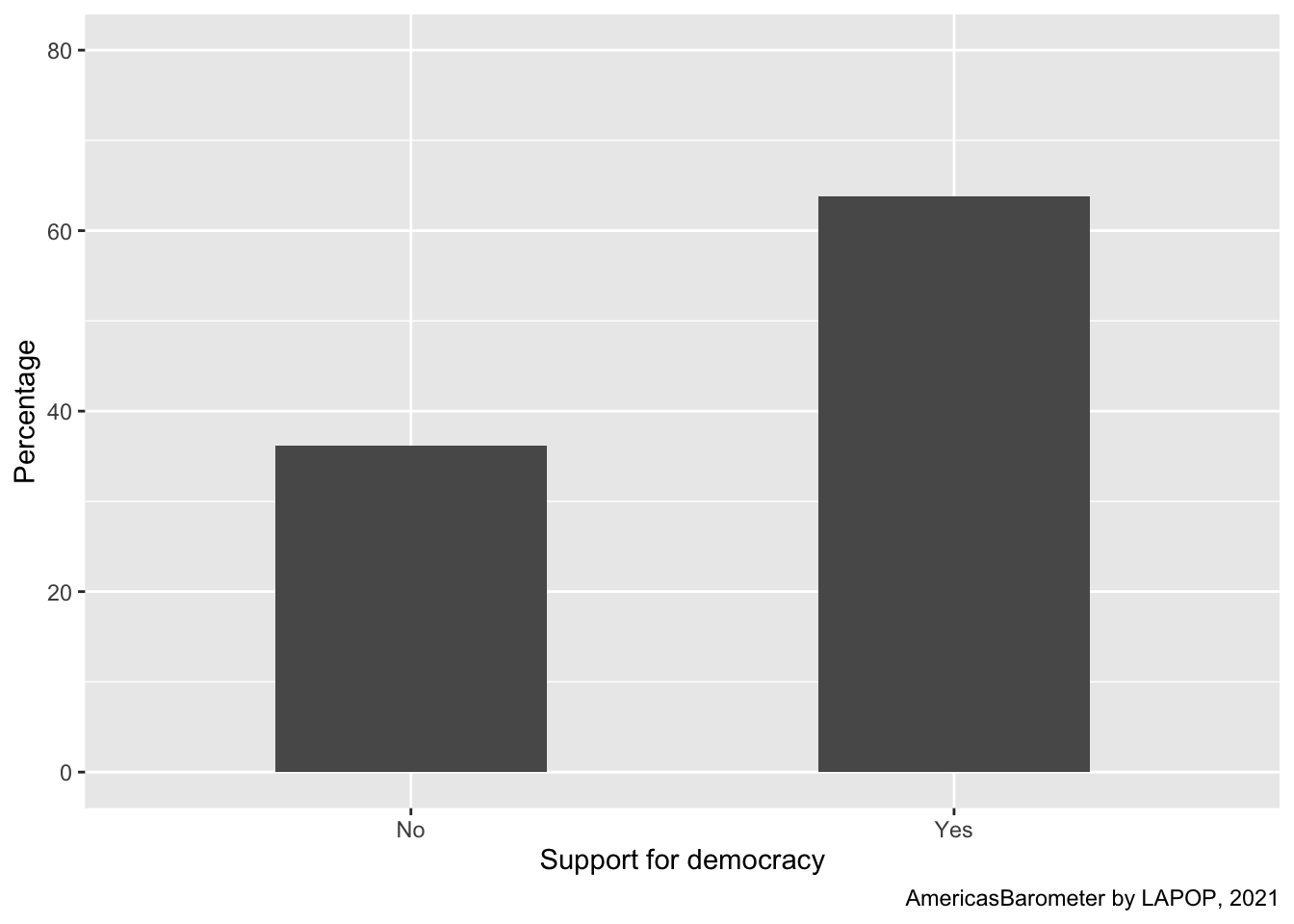
Up to this point, we have presented a bar plot of a single variable, support for democracy, for the whole sample, that includes all countries. Figure 1.1 shows the percentage of support for democracy by country. We will see this type of plot in a following section.

Social media users

Now, we are presenting an example of the report The Pulse of Democracy for the 2018/19 round. We follow similar procedures as the section above and we will replicate some figures of the report for the 2018/19 round. We are going to work with these variables: SMEDIA1. Do you have a Facebook account?; SMEDIA4. Do you have a Twitter account?; SMEDIA7. Do you have a WhatsApp account?. These questions have as answer options:

1. Yes

2. No

When reading the database in R, this program imports the variables as “num”, which most functions in R treat as numeric. These variables have to be converted to variables of type “factor” with the command as.factor, since they are categorical variables. We save these new variables in the dataframe. Here we have used the = operator which is similar to the <- operator that assigns a procedure to a new object of an R dataframe.

lapop18$smedia1r = as.factor(lapop18$smedia1)
lapop18$smedia4r = as.factor(lapop18$smedia4)
lapop18$smedia7r = as.factor(lapop18$smedia7)

These new variables of type factor have to be labeled with the command levels. A vector with concatenated labels is used, using the command c( ).

levels(lapop18$smedia1r) <- c("Yes", "No")
levels(lapop18$smedia4r) <- c("Yes", "No")
levels(lapop18$smedia7r) <- c("Yes", "No")

Calculating the variables of social network users

As we saw in a previous module, you can calculate new variables with conditional values of other variables using the ifelse command. In this way, we calculate the variables of social network users.

lapop18$fb_user <- ifelse(lapop18$smedia1==1 & lapop18$smedia2<=4, 1, 0)
lapop18$tw_user <- ifelse(lapop18$smedia4==1 & lapop18$smedia5<=4, 1, 0)
lapop18$wa_user <- ifelse(lapop18$smedia7==1 & lapop18$smedia8<=4, 1, 0)

Describing the variables

With the variables ready, we now proceed to make the general tables with the table command. Note the use of # as a way of making annotations, which are not R code.

table(lapop18$smedia1r) #Facebook

## 
##   Yes    No 
## 15389 11573

table(lapop18$smedia4r) #Twitter

## 
##   Yes    No 
##  2363 24558

table(lapop18$smedia7r) #Whatsapp

## 
##   Yes    No 
## 17446  9569

This table command gives us the absolute frequencies (number of observations) for each category of variables (in this case Yes and No). To get the relative frequencies, we will use the command prop.table, where the previous command table is nested.

prop.table(table(lapop18$smedia1r))

## 
##       Yes        No 
## 0.5707663 0.4292337

prop.table(table(lapop18$smedia4r))

## 
##        Yes         No 
## 0.08777534 0.91222466

prop.table(table(lapop18$smedia7r))

## 
##       Yes        No 
## 0.6457894 0.3542106

However, the command prop.table returns us too many decimal places and the relative frequencies on a scale of 0 to 1. To round this figure we use the round command, which allows us to specify the number of decimal places to be displayed. Both the table command and the prop.table are nested within this new command. In this case, we use 3 decimals, so when it is multiplied by 100, it remains in the form of a percentage with 1 decimal place.

round(prop.table(table(lapop18$smedia1r)), 3)*100

## 
##  Yes   No 
## 57.1 42.9

round(prop.table(table(lapop18$smedia4r)), 3)*100

## 
##  Yes   No 
##  8.8 91.2

round(prop.table(table(lapop18$smedia7r)), 3)*100

## 
##  Yes   No 
## 64.6 35.4

It is not practical to present 3 tables when the variables have the same response categories. For presentation purposes it might be better to build a single table. You can save the partial tables in new objects with the operator = and then join them as rows with the command rbind in a new dataframe “table” with the command as.data.frame, in such a way that the responses to each social network appear in rows.

Facebook = round(prop.table(table(lapop18$smedia1r)), 3)*100
Twitter = round(prop.table(table(lapop18$smedia4r)), 3)*100
Whatsapp = round(prop.table(table(lapop18$smedia7r)), 3)*100
tabla = as.data.frame(rbind(Facebook, Twitter, Whatsapp))
tabla

##           Yes   No
## Facebook 57.1 42.9
## Twitter   8.8 91.2
## Whatsapp 64.6 35.4

To have a better presentation of the table, you can use the kable command from the knitr package, using the table built above.

library(knitr)
knitr::kable(tabla, format="markdown")

	Yes	No
Facebook	57.1	42.9
Twitter	8.8	91.2
Whatsapp	64.6	35.4

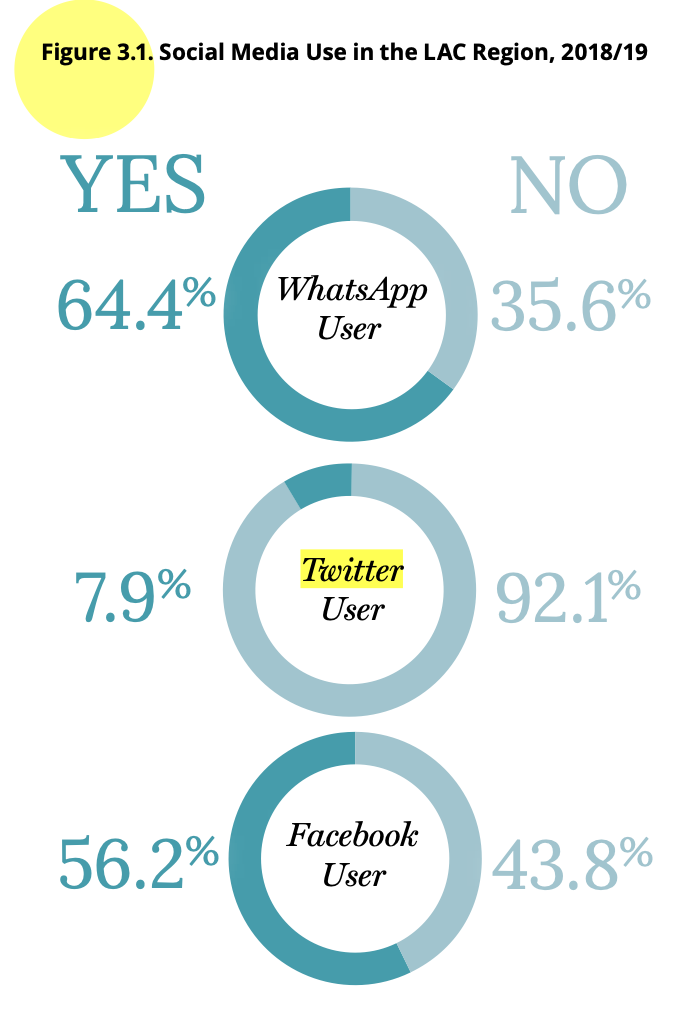
Plotting the variables

In Graph 3.1 of the report it is observed that these data are reported through a pie chart.

We can reproduce that graph using the pie command which is part of the basic R syntax. Within this command you can nest the table command to graph these values.

pie(table(lapop18$smedia1r))

You could also think of a bar chart. Using the basic R commands, you can use the barplot command.

barplot(prop.table(table(lapop18$smedia1r)))

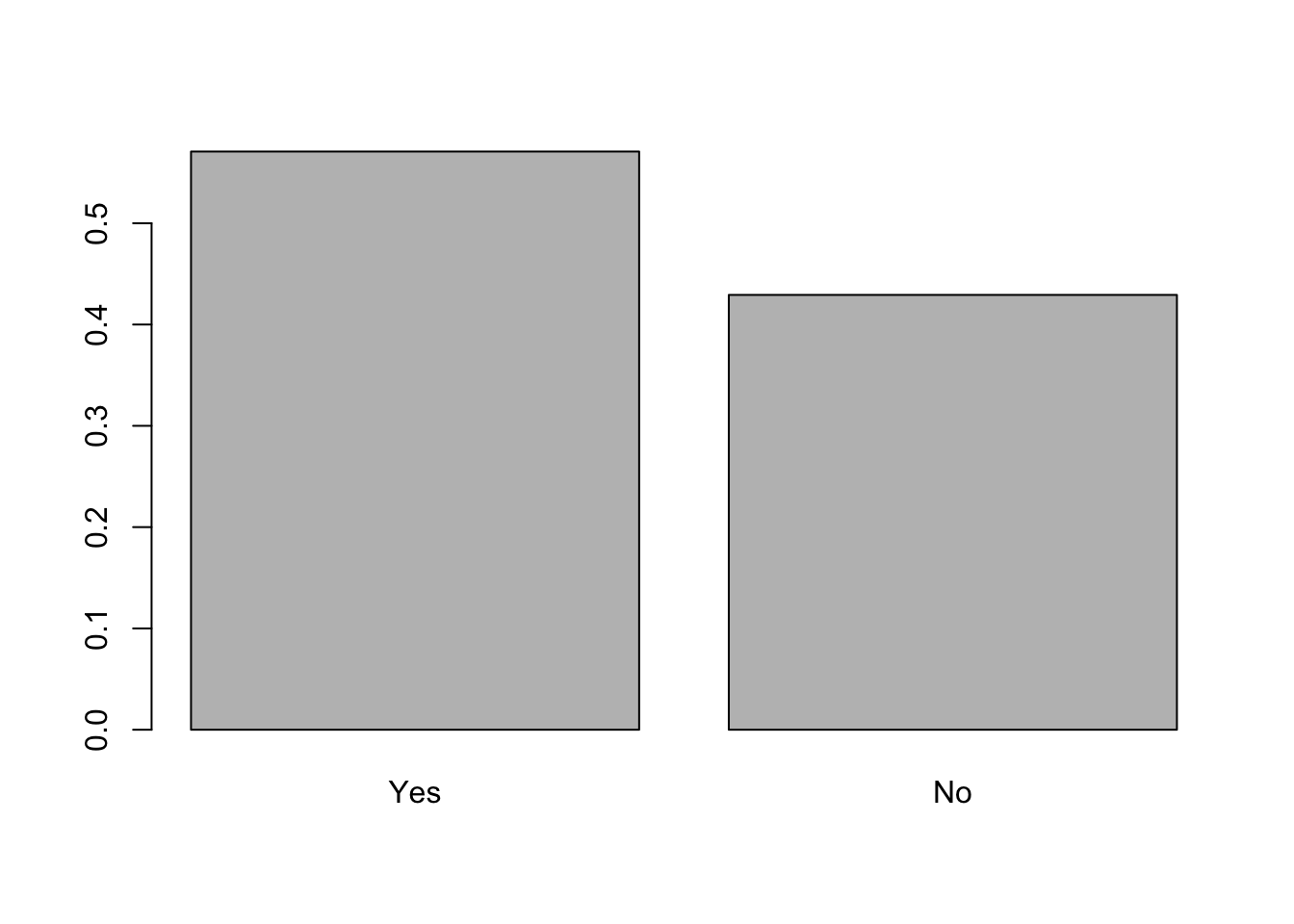
These graphical commands have options to adjust the graph, for example to include percentages and adjust scales. But, to have more graphical options, we can use the ggplot package to reproduce the pie chart.

In this example, we have to define first the data to be used. The subset command has been used again, but inside ggplot so that the command (internally) works with the variable but without the missing values. The !is.na () syntax prevents the command from including missing values of a variable in calculations. If data = lapop had been used the graph would have included a large sector corresponding to the proportion of NA. If !is.na () had been used outside of ggplot creating a new variable, all observations with missing values would have been removed, which would decrease the N, affecting future calculations.

The ggplot command works by adding layers. The aes specification is used to define the “aesthetics” of the graph. It is generally used to indicate which variable is going to be graphed on which axis (x or y). You can also use the fill = specification to define the groups to be generated.

After specifying the data and the axes, you have to specify the type of graph you want to make. This is done with geometries (“geom”). There is no direct geometry to make a pie chart, so you have to initially use a simple bar chart, using the command geom_bar (), where the width of the bar is defined internally. If we left the syntax at this point, a bar would be generated that would be divided by the values of the variable “smedia1r”. To generate the pie chart, you have to add another command coord_polar, which transforms the bar to polar coordinates, creating a pie chart.

library(ggplot2) #librería especializada en gráficos
ggplot(data=subset(lapop18, !is.na(smedia1r)), aes(x="", fill=smedia1r))+
  geom_bar(width=1) +
  coord_polar("y", start=0)

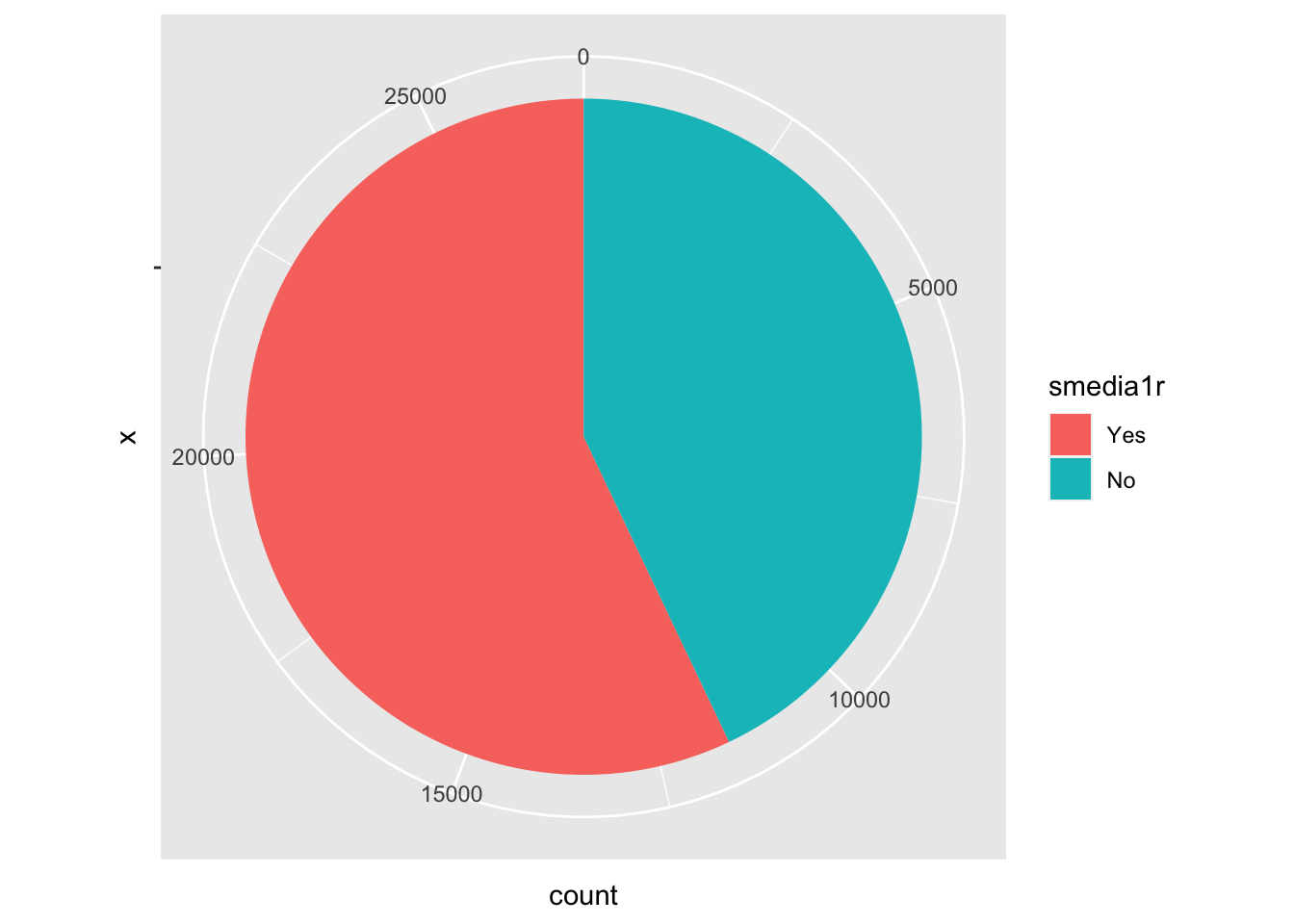
The above graph has started from the same dataframe “lapop18”, using the data from “smedia1r”. However, to better manipulate the graph it is easier to create a new dataframe with the aggregated data (frequencies and %). In other words, save the results data from the “smedia1r” table in a new dataframe. Then that new dataframe is used to make the pie graph with ggplot.

One aspect to note is that in this case the tidyverse is being used, which includes the pipe %>% command from the dplyr library, which is a (slightly) different way of writing code in R, in a concatenated way, step by step. A simple explanation of how the pipe is used can be found here.

The first thing to notice is that a new object called “df” is going to be created. Information coming from the dataframe “lapop18” will be stored in this object. The subset command is used to remove the missing values of “smedia1r” from the calculation of the percentages. Then (%>%), this data will be grouped by categories of the variable “smedia1r”. Next (%>%), in each group the total number of observations is calculated with the command summarise(n = n()). Finally (last step with %>%), with this total by groups the percentages are calculated and these percentages are saved in a new column “per”.

library(dplyr)
df = subset(lapop18, !is.na(smedia1r)) %>%
      group_by(smedia1r) %>% 
      dplyr::summarise(n = n()) %>%
      mutate(per=round(n/sum(n), 3)*100)
df

## # A tibble: 2 × 3
##   smedia1r     n   per
##   <fct>    <int> <dbl>
## 1 Yes      15389  57.1
## 2 No       11573  42.9

With this syntax, a table is created containing the total number of observations and the percentage for each category of the variable “smedia1r”. A more direct way to create the same data is to use the janitor library and the tabyl command. In R there are multiple ways to get to the same results.

library(janitor)
subset(lapop18, !is.na(smedia1r)) %>%
  tabyl(smedia1r)

##  smedia1r     n   percent
##       Yes 15389 0.5707663
##        No 11573 0.4292337

Once we have the table, we can use it to produce the pie chart with ggplot. Note that in this case the data used comes from the dataframe df (not from lapop18). This dataframe has a column called “per” with the respective percentages, which should be plotted on the Y-axis. As in the previous case, to make the pie chart, we start from the bar chart (hence geom_bar), which is then passed to polar coordinates (hence coord_polar).

A text layer is added, with the specification geom_text. Within this specification, an “aesthetic” is determined with the data label aes(label=...), where the percentage data “per” and the symbol “%” are joined with the paste command, with a space (sep=...) between them. Set the font color with color="...", sets to white to contrast with the colors of the pie chart. With the command hjust=... the horizontal position of this text is adjusted. The ggplot command can include various “themes” for the plot. In this case, theme_void() has been used, which indicates an empty background. Finally, with the specification scale_fill_discrete(name=...) you can change the title of the legend so that it does not show the name of the variable, but a more suitable label.

ggplot(data=df, aes(x="", y=per, fill=smedia1r))+
  geom_bar(width=1, stat="identity")+
  geom_text(aes(label=paste(per, "%", sep="")), color="white",
            position=position_stack(vjust=0.5), size=3)+
  coord_polar("y")+
  theme_void()+
  scale_fill_discrete(name="Do you have a Facebook account?")

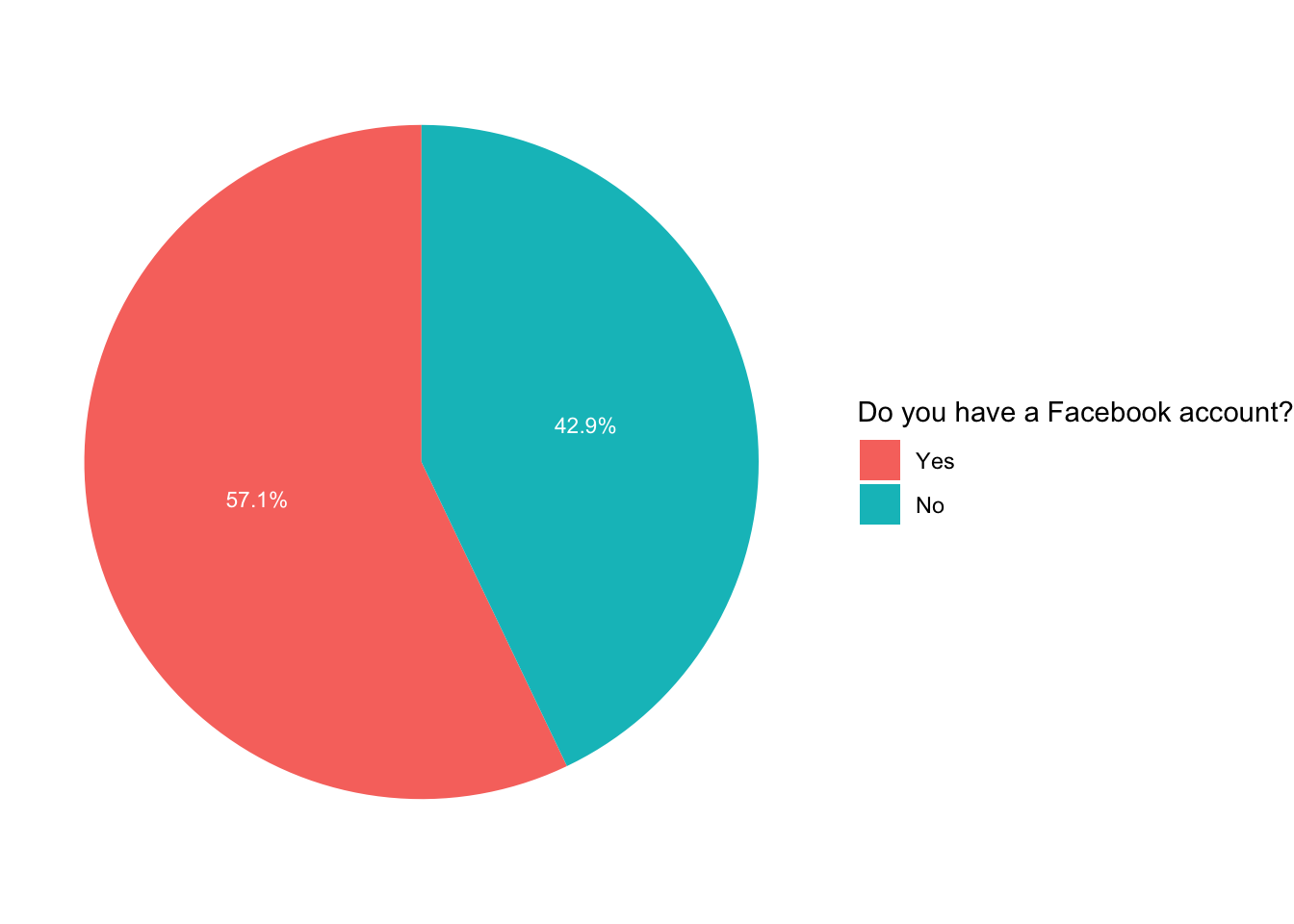
If instead of a pie chart you want to display a bar chart, with the data from the “lapop18” dataframe you can use the following code. Unlike the first pie chart, the aes(..) specification now includes the variable “smedia1r” as the variable to be plotted on the X-axis. Inside the geometric object geom_bar() it is indicated that the bar must represent the proportions in percentages aes(y=..prop..*100, group=1). In this example, a general label for the graph and for the axes has been included with the labs(...) command. In this command you can also add a “caption” to indicate the source of the data. Finally, the specification coord_cartesian(ylim=c(0,60)) limits the Y axis to values between 0 and 60.

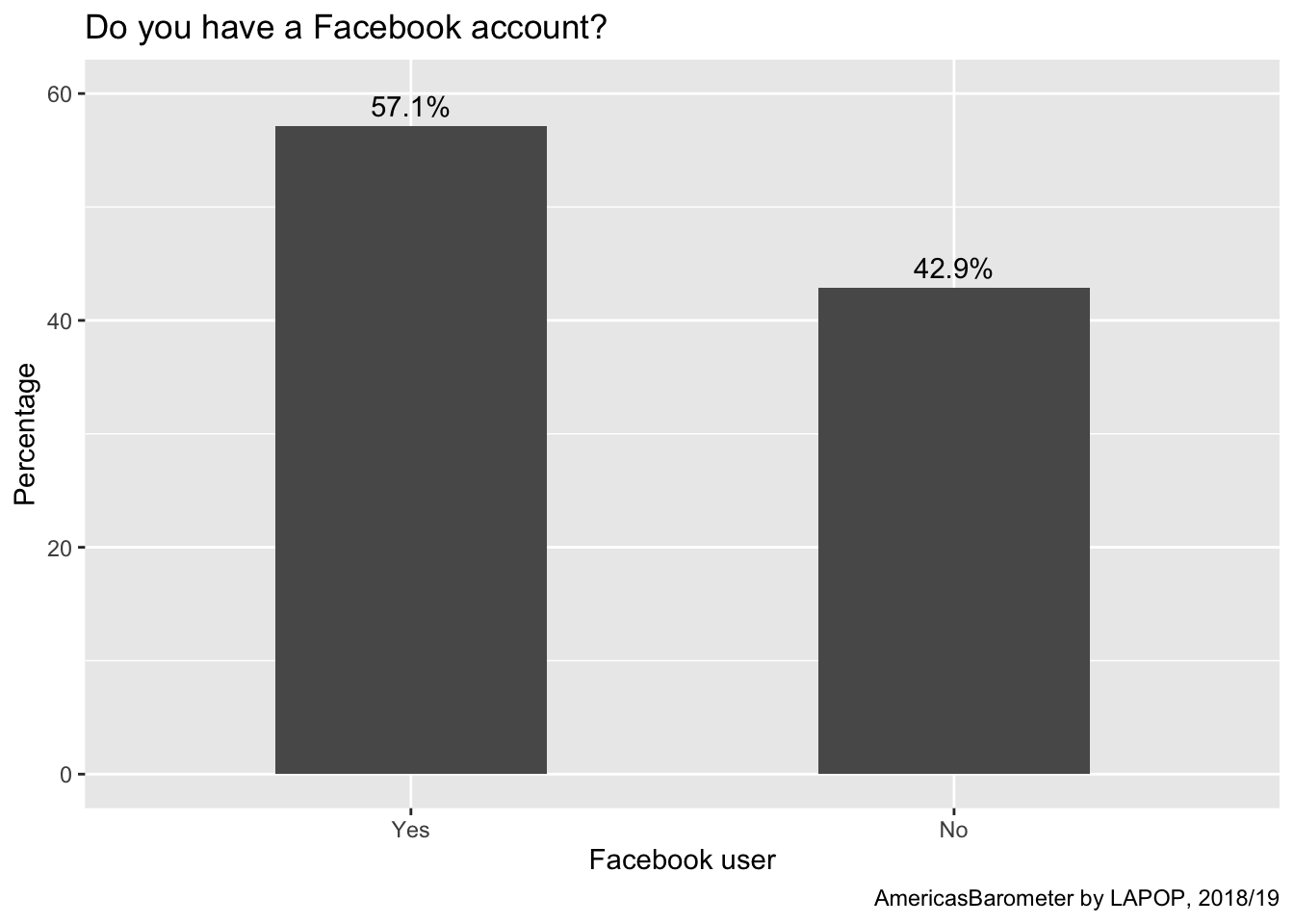
ggplot(data=subset(lapop18, !is.na(smedia1r)), aes(x=smedia1r))+
  geom_bar(aes(y=..prop..*100, group=1), width=0.5)+
  labs(title="Do you have a Facebook account?", x="Facebook user", y="Percentage", caption="AmericasBarometer by LAPOP, 2018/19")+
  coord_cartesian(ylim=c(0, 60))

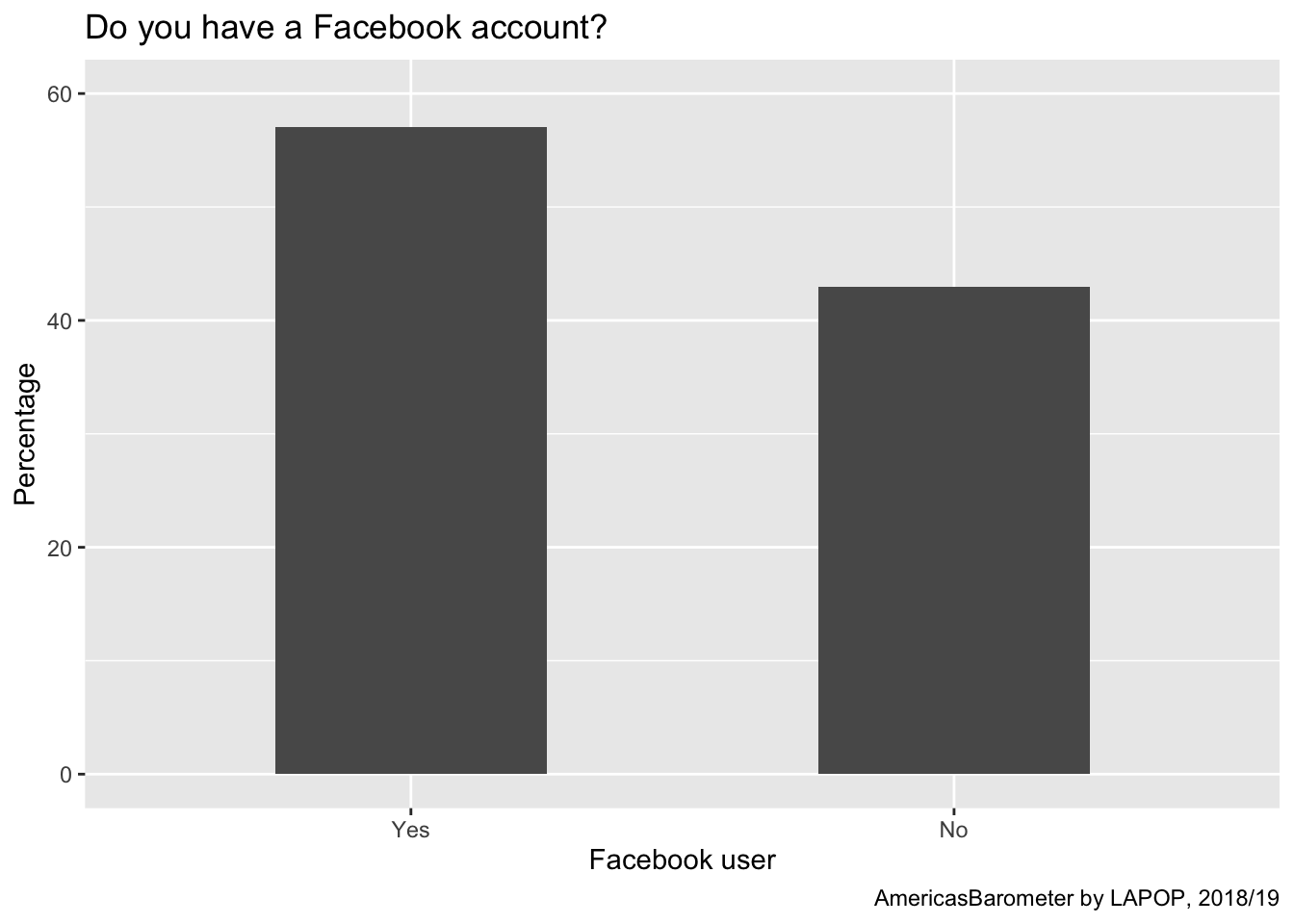
In this case you can also use the grouped data of the “df” dataframe. Unlike the previous option, in “df” there is the percentage data, so it should not be calculated in the code, so in the aesthetics specification it indicates that the alternatives should be shown on the X axis of the variable “smedia1r” and on the Y axis the percentage, in this way aes(x=media1r, y=per). For this reason also in the geom_bar specification, now instead of requiring the calculation of the percentage, it is only indicated to replicate the data (with stat="identity") from aes. Finally, in this case we add the text layer to include the percentages in each column, with the geom_text specification.

ggplot(df, aes(x=smedia1r, y=per))+
  geom_bar(stat="identity",  width=0.5)+
  geom_text(aes(label=paste(per, "%", sep="")), color="black", vjust=-0.5)+
  labs(title="Do you have a Facebook account?", x="Facebook user", y="Percentage", caption="AmericasBarometer by LAPOP, 2018/19")+
  coord_cartesian(ylim=c(0, 60))

We consider this option a easier way to work with this data. First, we have to create a dataframe with the percentages and the labels. Then, we have to use this dataframe in ggplot. In the following sections, we will use this way.

Summary

In this document we have worked with nominal categorical variables, such as whether or not you suppport democracy or whether or not you use social networks. We present several ways to describe these variables in frequency tables and to plot these variables, using circular or bar graphs.

Calculations including design effect

The results for the 2018/19 wave are not exactly the same as those in the report, since LAPOP includes the effect of the sample design in its calculations. According to this syntax, it is found that 57.1% of interviewees report being a Facebook user, when 56.2% appear in the report. The same with Twitter, which here is calculated at 8.8% and in the report 7.9%; and with WhatsApp that appears here with 64.6% and in the report with 64.4%. As indicated in the section on the use of survey weights using data from the AmericasBarometer (available here), there are several ways to reproduce the results by incorporating the survey weights. A first option is to use the command freq, which allows the inclusion of a weighting variable, such as “weight1500”. The plot=F specification is included to not produce the bar graphs.

library(descr)
descr::freq(lapop18$fb_user, lapop18$weight1500, plot = F)

## lapop18$fb_user 
##       Frequency Percent Valid Percent
## 0         11337  41.988         43.77
## 1         14564  53.939         56.23
## NA's       1100   4.073              
## Total     27000 100.000        100.00

descr::freq(lapop18$tw_user, lapop18$weight1500, plot = F)

## lapop18$tw_user 
##       Frequency Percent Valid Percent
## 0         23819  88.220        92.023
## 1          2065   7.647         7.977
## NA's       1116   4.133              
## Total     27000 100.000       100.000

descr::freq(lapop18$wa_user, lapop18$weight1500, plot = F)

## lapop18$wa_user 
##       Frequency Percent Valid Percent
## 0          9252  34.266         35.63
## 1         16714  61.903         64.37
## NA's       1035   3.832              
## Total     27000 100.000        100.00

Without considering the survey weights, 57.1% of the interviewees have a Facebook account. This percentage varies to 55.2% if the expansion variable is included, which is the value shown in the report. These weighted results can also be saved to objects and then graphed in the same way as the unweighted results.

In the case of Facebook, the table can be saved as a dataframe, using the command as.data.frame. This table includes data that we do not require, such as the NA’s and Total row and the Percent column. These rows and this column are deleted using the specification [-c(3,4), -2].

The columns are then renamed to avoid the “Valid Percent” name. They are simply named “freq” and “per”. This column “per” is the one that has the data that we will graph. Finally, a “lab” column is added with the labels of each row of results.

fb <- as.data.frame(descr::freq(lapop18$fb_user, lapop18$weight1500, plot = F))
fb = fb[-c(3,4), -2]
colnames(fb) = c("freq", "per")
fb$lab = c("No", "Yes")
fb

##       freq      per lab
## 0 11336.69 43.77052  No
## 1 14563.60 56.22948 Yes

With this new dataframe we can replicate the same codes used above to make a bar chart or a pie chart. The following code displays the bar chart. Note that now the “fb” dataframe is used and that in aes it is specified that the data from the “lab” column must be on the X axis and the data from the “per” column must be on the Y axis.

ggplot(data=fb, aes(x=lab, y=per))+
  geom_bar(stat="identity",  width=0.5)+
  geom_text(aes(label=paste(round(per, 1), "%", sep="")), color="black", vjust=-0.5)+
  labs(title="Do you have a Facebook account?", x="Facebook user", 
       y="Percentage", caption="AmericasBarometer by LAPOP, 2018/19")+
  coord_cartesian(ylim=c(0, 60))

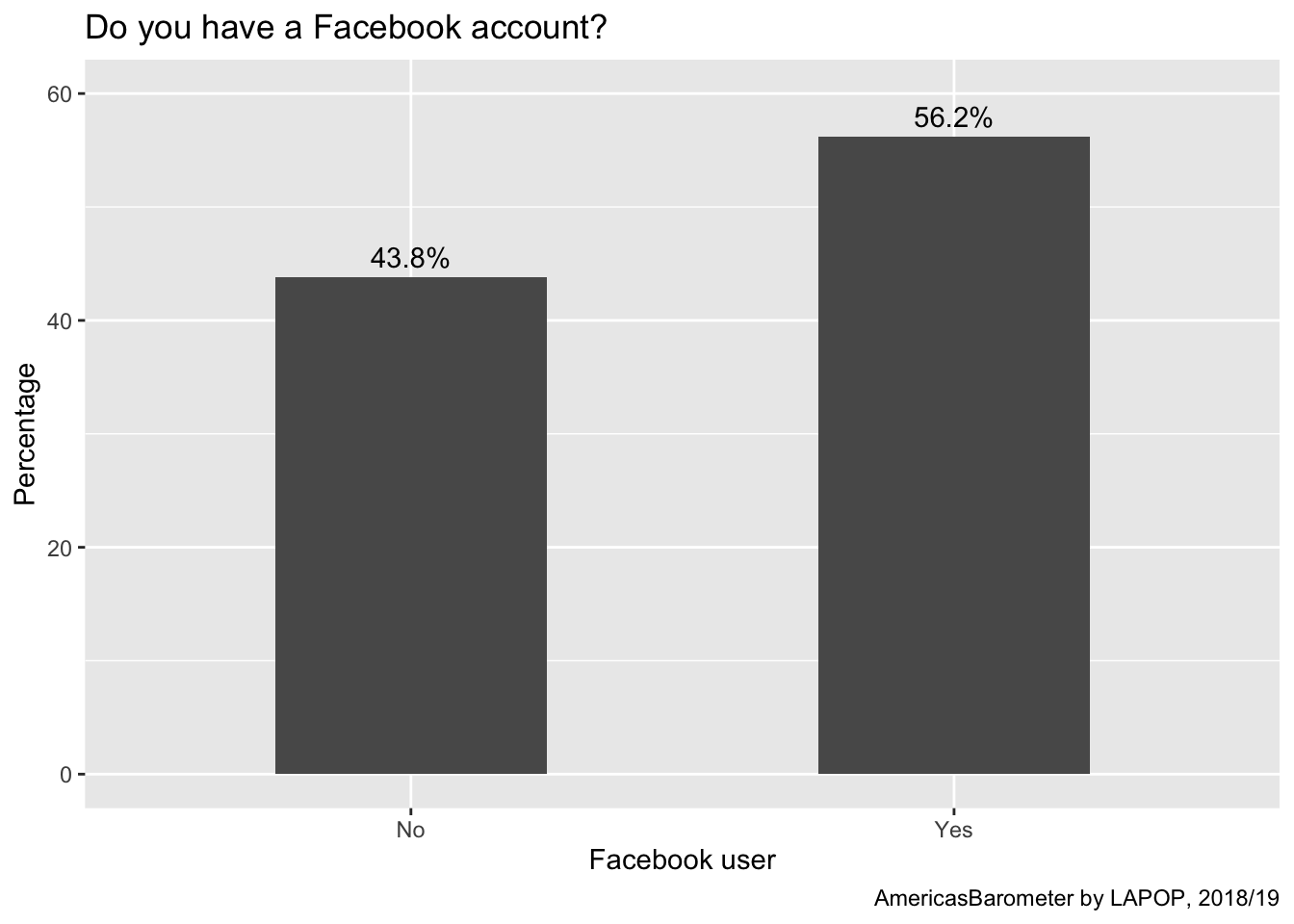
The same can be done to create a pie chart. This graph reproduces the results found in Graph 3.1 of the report.

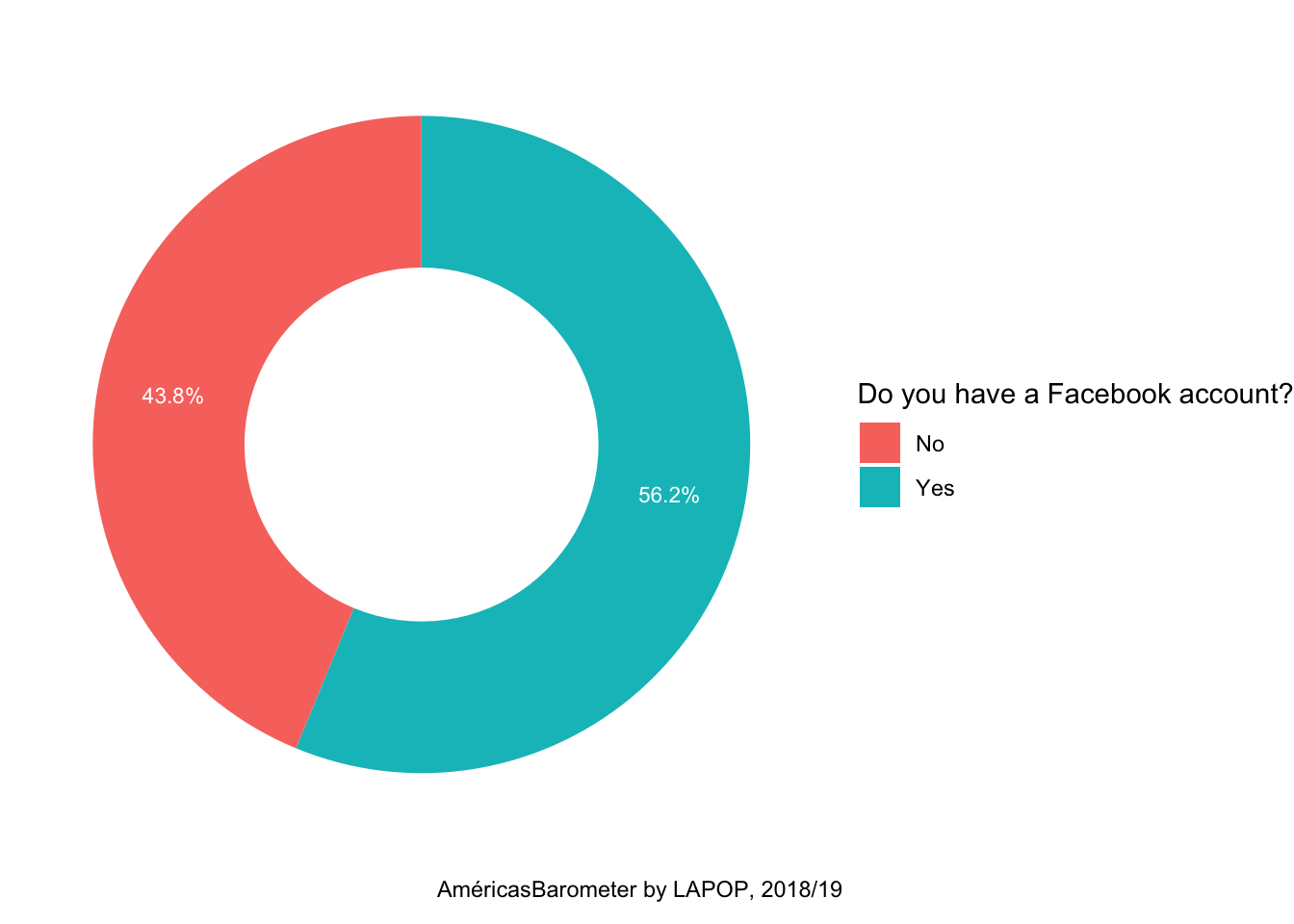
ggplot(data=fb, aes(x=2, y=per, fill=lab))+
  geom_bar(stat="identity")+
  geom_text(aes(label=paste(round(per, 1), "%", sep="")), color="white", 
            position=position_stack(vjust=0.5), size=3)+
  coord_polar("y")+
  theme_void()+
  labs(caption="AméricasBarometer by LAPOP, 2018/19")+
  scale_fill_discrete(name="Do you have a Facebook account?")+
  xlim(0.5, 2.5)

The second option to reproduce the results in the report is using the package survey. As we indicate in this section, we have to define first the sample design with the command svydesign.

library(survey)
lapop.design = svydesign(ids = ~upm, strata = ~estratopri, weights = ~weight1500, nest=TRUE, data=lapop18)

Once you have created the data with the expansion factor in the “lapop.design” object, you can use the native commands of the package survey to perform calculations. For example, to calculate the frequency distribution table you can use the svytable command.

svytable(~fb_user, design=lapop.design)

## fb_user
##        0        1 
## 11336.69 14563.60

These frequencies can be nested in the prop.table command to calculate the percentages of social network users. These results are the same as those shown in the previous graphs and those that appear in the report.

These data can also be saved in a dataframe that is adapted for graphing, following the same procedure as in the previous graphs.

prop.table(svytable(~fb_user, design=lapop.design))

## fb_user
##         0         1 
## 0.4377052 0.5622948

prop.table(svytable(~tw_user, design=lapop.design))

## tw_user
##          0          1 
## 0.92023002 0.07976998

prop.table(svytable(~wa_user, design=lapop.design))

## wa_user
##         0         1 
## 0.3563091 0.6436909